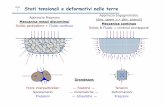
Stati tensionali e deformativi nelle terre

Grandezze:

← Statiche →← Cinematiche →

← Idrauliche →

Approccio RigorosoMeccanica mezzi discontinui

Solido particellare + Fluido continuo

Forze interparticellariSpostamenti

Pressioni

TensioniDeformazioni

Pressioni

Approccio IngegneristicoMeccanica continuo

Solido & Fluido = continui sovrapposti

MdC1

I vettori t e d sono legati tra loro dal legame costitutivo del mezzo

Tensione e deformazione nel mezzo continuo

0limA

FtAδ

δδ→

=

0lim

l

sdlδ

δδ→

=

Mezzo continuo alla Cauchy

Vettore ( tensore) tensione Vettore ( tensore) deformazione

Se il mezzo è indeformabile (d ≡ 0) il legame costitutivo è di tipo rigido

MdC2

Componenti normali e tangenziali

Componenti NormaliCompressione → Contrazione

Componenti TangenzialiTaglio → Distorsione

0limA

NAδ

δσδ→

=0

limA

TAδ

δτδ→

=

Nδ

wδTδ

uδu

wv

x

z

y

0lim

l

wlδ

δεδ→

=0

liml

ulδ

δγδ→

=

Tensione

Deformazione

• In mecc. delle terre prevalgono i fenomeni di compressione ad essi si attribuisce segno positivo. • Per applicare le stesse convenzioni della Scienza delle Costruzioni occorre orientare

la normale verso l’interno dell’elemento

lδ lδ

MdC3

Componenti cartesiane

Riferimento: sistema cartesiano (x, y, z)(1° pedice → direzione normale, 2° pedice → direzione componente)

N. B.: le componenti sono dipendenti dal sistema di riferimento!

[ ]x xy xz

yx y yz

zx zy z

σ τ τσ τ σ τ

τ τ σ

=

[ ]x xy xz

yx y yz

zx zy z

ε γ γε γ ε γ

γ γ ε

=

Tensori

Equilibrio statico alla traslazione → Equazioni di continuità (Cauchy)

zW

x

zy

(Wx, Wy, Wz = componenti forze di massa lungo x, y, z)

=−∂σ∂

+∂

τ∂+

∂τ∂

=−∂

τ∂+

∂

σ∂+

∂

τ∂

=−∂τ∂

+∂

τ∂+

∂σ∂

0

0

0

zzyzxz

yzyyxy

xzxyxx

Wzyx

Wzyx

Wzyx

xzτ xzxz dx

xττ ∂

+ ⋅∂

yzτ

yzyz dy

yτ

τ∂

+ ⋅∂

zσ

zz dz

zσσ ∂

+ ⋅∂

MdC4

Equilibrio statico alla rotazione

⇓reciprocità tensioni tangenziali

τ=ττ=ττ=τ

zyyz

xzzx

xyyx

Definizione

⇓reciprocità deformazioni tangenziali

γ=γγ=γγ=γ

zyyz

xzzx

xyyx

Simmetria dei tensori rispetto alla diagonale

⇓esiste un sistema di riferimento (‘principale’) in cui il tensore è diagonale

Sistema principale delle tensioni⇔ τxy = τyz = τxz = 0

Proprietà di simmetria e reciprocitàMdC5

Rappresentazione sul piano di Mohr

( ),n nmT σ τ

t

τ

Pnmτ

nσ σ

• estremo posteriore del vettore = polo P del cerchioSe si orienta la normale uscente secondo l’asse σ:

Ciò corrisponde a: σ > 0 se di compressione, τ >0 se antioraria.

• punto T rappresentativo di (σn, τnm) = simmetrico di P rispetto all’asse σ

Il cerchio di Mohr descrive la variazione di componenti normali e tangenzialicon la direzione della normale all’elemento di volume in un piano.

( ),m mnS σ τ

mσmnτ

• punto S rappresentativo di (σm, τmn) = simmetrico di T rispetto al centro

MdC6

3σ≡σv

Stati tensionali tipici e cerchi di Mohr

1

2

4

5

Compressione isotropa

Compressione anisotropa

Compressione e taglio

P

vh σ=σ

τ

σ

HP ≡

τ

σ

3σ≡σh

5

Taglio puro

τ

σ

1σ3σ

VP =4

τ

σ

3σ1σ

1σ≡σv

V

HP ≡

1σ≡σhH

P

V

1

2

τ

σ3

3

vσ

V

hσH

MdC7

Componenti principali di tensione e deformazione

Riferimento: sistema principale (1, 2, 3)[pedice 1/2/3 → tensione (deformazione) principale massima/media/minima]

1

2

3

0 00 00 0

σσ

σ

Tensoridiagonali

1

2

3

0 00 00 0

εε

ε

1σ

3

21

2σ

3σ

Valori e coseni direttori (n1, n2, n3) di tensioni principali si ottengono imponendo soluzione non banale al sistema σ{n}=[σ]{n}, il che richiede:

0det =

σ−στττσ−στττσ−σ

zzyzx

yzyyx

xzxyx

MdC8

L’annullamento del determinante corrisponde alla soluzione dell’equazione di III grado:

(I1, I2, I3 = invarianti* di tensione del 1°, 2°, 3° ordine)

0322

13 =−σ⋅+σ⋅−σ III

321222

3

323121222

2

3211

2 σσσ≡τττ+τσ−τσ−τσ−σσσ=

σσ+σσ+σσ≡τ−τ−τ−σσ+σσ+σσ=

σ+σ+σ≡σ+σ+σ=

xzzyxyyxzxzyyzxzyx

yzxzxyxzzyyx

zyx

I

I

I

Analogamente per le deformazioni:

0322

13 =−ε⋅+ε⋅−ε EEE

(E1, E2, E3 = invarianti* di deformazione del 1°, 2°, 3° ordine)

( )( ) 321

2223

323121222

2

3211

41

41

41

εεε≡γγγ+γε−γε−γε−εεε=

εε+εε+εε≡γ−γ−γ−εε+εε+εε=

ε+ε+ε≡ε+ε+ε=

xzzyxyyxzxzyyzxzyx

yzxzxyxzzyyx

zyx

E

E

E

*invarianti = non dipendono dal sistema x, y, z

Invarianti di tensione e deformazioneMdC9

Componenti ottaedrali e invarianti di tensione

Piano ottaedrale = piano ortogonale alla trisettrice del quadrante 1, 2, 3(coseni direttori n1 =n2 =n3 = √3/3)

Proiettando le σ1, σ2, σ3

(⇔ considerando l’equilibrio del tetraedro):

( ) ( ) ( ) 221

232

231

221

1321

332

31

33

II

I

oct

oct

−=σ−σ+σ−σ+σ−σ=τ

=σ+σ+σ

=σ

p = tensione media3

321 σ+σ+σ=σ= octp

q = tensione deviatorica ( ) ( ) ( )2322

312

2121

23

σ−σ+σ−σ+σ−σ=τ= octq

221

1

3

3

IIq

Ip

−=

=⇒ p, q = invarianti di tensione

Con queste due sole componenti tensionali, è possibile descrivere lo stato medio di compressione e di taglio agente sull’elemento

MdC10

Componenti ottaedrali e invarianti di deformazione

Nel riferimento principale per le deformazioni, proiettando ε1, ε2, ε3:

( ) ( ) ( ) 221

232

231

221

1321

33

2232

33

EE

E

oct

oct

−=ε−ε+ε−ε+ε−ε=γ

=ε+ε+ε

=ε

εv = deformazione volumetrica

εs = deformazione distorsionale

221

1

332 EE

E

s

v

−=ε

=ε⇒ εv, εs = invarianti di deformazione

( ) ( ) ( )2322

312

2132

2ε−ε+ε−ε+ε−ε=

γ=ε oct

s

3213 ε+ε+ε=ε=ε octv

Con queste due sole componenti deformative, è possibile descrivere le variazioni di volume e di forma dell’elemento

MdC11

Problema tensio-deformativo piano

Ipotesi tipica: ogni piano verticale (x, z) è di simmetria

⇓• stato di deformazione piano ⇒ εy = γyz = γxy = 0

• in ipotesi di mezzo elastico ⇒ τyz = τxy = 0

•σ = tensione principale σ2 (indipendente da y)

Problemi tipo

prove di taglio muri di sostegno travi di fondazione

MdC12

2231 ε+ε

=εv

Problema tensio deformativo piano

dL = lavoro di deformazione per unità di volume = σ1∙dε1 + σ2∙dε2 + σ3∙dε3

Cerchi di Mohr di stato piano

tensioni deformazioni

dε2 = 0 ⇒ 1 1 3 3 ..... vL s t γδ σ δε σ δε δε δε= ⋅ + ⋅ = = ⋅ + ⋅

1σ2

31 σ−σ=t

τ

σ3σ

231 σ+σ

=s

2231 ε−ε

=εγ

1ε

2γ

ε3ε

s (= ascissa del centro) = tensione media nel piano

t (= raggio del cerchio) = tensione deviatorica nel piano

MdC13

Problema tensio deformativo assialsimmetrico

Ipotesi: l’asse verticale (z) è di simmetria radiale

⇓• ovunque ε2 = ε3 e σ2 = σ3

• in asse τ = 0 ⇒ direzioni principali = orizzontale e verticale(questo non è verificato in generale altrove)

Problemi tipo

prove di compressione palifondazioni circolari

MdC14

Problema tensio deformativo assialsimmetrico

dL = lavoro di deformazione per unità di volume = σ1∙dε1 + σ2∙dε2 + σ3∙dε3

σ2 = σ3 , dε2 = dε3 ⇒ 1 1 3 32 ..... v sL p qδ σ δε σ δε δε δε= ⋅ + ⋅ = = ⋅ + ⋅

tensioni deformazioni

1σ

τ

σ23 σ=σ 1ε

2γ

ε23 ε=ε

Cerchi di Mohr di stato assialsimmetrico

MdC15