Corso di FluidodinamicaAnno accademico 2010/2011

Prof. Tommaso Astaritaastarita@unina.it

Tel. 081 7685184

MATERIALE DIDATTICOGasdinamica, Giovanni M. Carlomagno, ed. Liguori, 2009

Appunti e Slides dal sito www.docenti.unina.it

wpage.unina.it/astarita

RICEVIMENTO ALLIEVI

Martedì 16:00-18:00

Mercoledì 16:00-18:00

(X piano - p.le Tecchio 80)

STUDIO DI UN FENOMENO FISICO

Descrizione del fenomeno

Identificazione delle ipotesi e delle approssimazioni

Modellazione del fenomeno e individuazione delle variabili

Applicazione dei principi e delle leggi fisiche

Scrittura delle equazioni che governano il fenomeno

Risoluzione delle equazioni con le condizioni al contorno

Verifica della qualità e della validità dei risultati

LEGGI FONDAMENTALI DELLA TERMODINAMICA CLASSICA

Legge zero 0 >T I legge L δ Q δdEt =

II legge S;δ+ Sδ=dS ie

0 Sδ ; Q/T δS ie =

Postulato di Nernst 0= S lim0T

SISTEMA TERMODINAMICO

Un sistema termodinamico si può definire in termini di un volume dicontrollo V (formulazione Euleriana) o di una massa di controllo (formulazione Langrangiana).

Formulazione euleriana

V è fisso nel tempo

V può essere pluri o semplicemente connesso

D sono superfici chiuse, materiali, o fittizie

La massa contenuta in V è, in generale, funzione del tempo

L'estensione è fissata in termini del volumedel sistema V

Formulazione lagrangiana

è fissa nel tempo.

Le dimensioni di V, (forma e locazione) possono variare nel tempo.

La superficie D delimitante il volume Voccupato dalla massa di controllo varia (in forma e dimensioni) nel tempo.

La connessione di V può variare nel tempo.

L'estensione del sistema e fissata in termini della massa del sistema

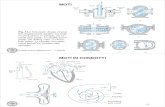
ESEMPI DI SCELTA DEL SISTEMA DI CONTROLLO

Formulazione Euleriana(sistema a volume costante;il tratto di condotto rigido)

Formulazione Lagragiana(sistema a massa costante;

il gas nel palloncino deformabile)

GRANDEZZE ESTENSIVE

n

1= iitot G= G

Una grandezza G si dice estensiva se il suo valore, in un sistema in cui èdistribuita in modo uniforme, è linearmente proporzionale all'estensionedel sistema stesso.

Se G è funzione solo di altre grandezze estensive G = f(Gi ); (i = 1, 2, .., k),essa è una funzione omogenea di primo grado nelle Gi

G gode inoltre della proprietà di additività

Sono grandezze estensive: il volume, la massa, il numero di moli, la quantitàdi moto, l'energia cinetica, l'entropia, l'energia interna, etc

Una funzione si dice omogenea di grado se, moltiplicando le variabili dacui dipende per uno stesso fattore > 0, essa risulta moltiplicata per ;ad esempio: f(x, y) = f (x,y); y = x2 y(x2x2.

UNIFORMITÀ DI UNA GRANDEZZA ESTENSIVA

Il concetto di distribuzione uniforme di una grandezza estensivarappresenta il grado di omogeneità con il quale la grandezza estensiva èdistribuita all’interno di un sistema

Definizione ingegneristica di uniformità: Dato un sistema di volume V , losi suddivida in un numero arbitrario n di sottosistemi (con n interopositivo) ciascuno di volume V = V /n. Il valore di una qualsiasigrandezza estensiva G in ciascuno dei sottosistemi sarà pari a Gi (i = 1, ..,n) e in generale diverso da sottosistema a sottosistema.

Indicando rispettivamente con Gmax e Gmin il valore massimo e il valoreminimo degli n valori Gi, la massima differenza tra i valori dei Gi neidiversi sottosis-temi potrà quindi essere individuata dalla quantità:

minmax GGG =

L’uniformità del sistema sarà senz’altro assicurata se, qualunque sia ilvalore di n, cioé la suddivisione fatta, è sempre verificata la condizione:

0 iGG /

GRANDEZZE INTENSIVE

Una grandezza intensiva I è una grandezza il cui valore (in un sistemauniforme) non dipende dall'estensione del sistema stesso.

Una grandezza intensiva è omogenea di grado zero in grandezze intensive.

La temperatura, la pressione e la velocità di un fluido sono esempi digrandezze intensive

GRANDEZZE SPECIFICHE

Una grandezza specifica è una grandezza estensiva riferita all'unità diestensione infinitesima.

Una grandezza estensiva G si può rendere specifica rispetto a qualsiasi altragrandezza estensiva G' di riferimento che caratterizzi l'estensione delsistema.

Nella maggior parte dei casi G' si identifica con la massa, o con il volume.

GRANDEZZE SPECIFICHEG riferita all'unità di massa si indicherà con g (densità massica di G).

G riferita all'unità di volume con g+ (densità volumetrica di G).

Tutte le grandezze specifiche riferite all'unità di massa si indicano con lalettera minuscola corrispondente a quella (maiuscola) con la quale si indica lagrandezza estensiva.

Per le grandezze specifiche riferite all'unità di volume, alla lettera minuscola

si appone l'apice +.

Fa eccezione la densità volumetrica di massa, o più sinteticamente densità di massa (massa riferita all'unità di volume), che si indica con la lettera greca .

Ad esempio, la grandezza estensiva entropia si indica con S, l'entropia perunità di massa con s e quella per unità di volume con s+.

Valgono le relazioni:

ρg = g ; +g v= g ; 1

= v

ρ= Δ

Δ

0Δ lim

V

V

GRANDEZZE SPECIFICHE

Le dimensioni di una grandezza specifica sono:

G

g 3

L

gG

Le grandezze specifiche g e g+ conservano lo stesso ordine tensorialedelle grandezze dalle quali vengono derivate.

La densità, il volume specifico, l'energia cinetica, per unità di massa o perunità di volume del fluido, sono esempi di grandezze specifiche.

La velocità, già indicata come grandezza intensiva, se intesa come quantitàdi moto per unità di massa, rappresenta anch’essa una grandezza specifica.

;

GRANDEZZE SCALARI, VETTORIALI, TENSORIALI

Una grandezza scalare (o, più semplicemente, uno scalare) è descritta ecaratterizzata in modo completo, in un prescelto sistema di unità di misura, daun numero (positivo o negativo).

Le grandezze scalari sono invarianti rispetto ad una qualunque trasformazionedel sistema delle coordinate di riferimento. Esempi sono: la massa, il volume, latemperatura, la densità, il volume specifico, la pressione in un fluido in quiete.

Uno scalare è anche definito come un tensore di ordine zero.

Una grandezza vettoriale (o, un vettore) è descritta e caratterizzata in modocompleto da un valore numerico e da una direzione orientata.

Una grandezza vettoriale può essere considerata come somma di tre vettoridiretti secondo tre direzioni di riferimento prefissate, le cui intensità vengonochiamate componenti (3 scalari) della grandezza stessa

Se le direzioni prefissate sono costanti per ogni punto dello spazio, il sistema diriferimento si dice cartesiano e, se in particolare queste direzioni sonomutuamente ortogonali, il sistema viene detto cartesiano ortogonale

GRANDEZZE SCALARI, VETTORIALI, TENSORIALI

Una grandezza vettoriale è detta assoluta se essa è invariante rispetto alsistema di riferimento; non saranno ovviamente tali le sue componenti.

Esempi di grandezze vettoriali, non necessariamente assolute, sono: leforze applicate, la velocità, l'accelerazione, la quantità di moto, la velocitàangolare, etc.

Un vettore è anche definito come un tensore di ordine uno e vienegeneralmente indicato con una sottolineatura V.

Una grandezza tensoriale del secondo ordine (o, più semplicemente, untensore) è una grandezza fisica associata agli enti geometrici punto,direzione orientata e giacitura orientata (ovvero punto e due direzioniorientate, potendosi rappresentare la giacitura con la direzione normale allagiacitura stessa). Essa viene generalmente indicata con due sottolineature.

GRANDEZZE SCALARI, VETTORIALI, TENSORIALI

In uno spazio a 3 dimensioni ci sono 3 giaciture indipendenti (pianicoordinati), per cui un tensore ha tre componenti vettoriali (non assolute)associate a ciascuna delle tre giaciture.

Alternativamente, poiché in uno spazio a 3 dimensioni ci sono 3 3 = 9coppie indipendenti di direzioni di riferimento (coppie coordinate), iltensore ha nove componenti scalari (anche esse non assolute), associate aciascuna delle coppie coordinate.

Tutte le grandezze associate ad un punto ed a due direzioni orientate sonograndezze tensoriali del secondo ordine che vengono indicate con unadoppia sottolineatura.

Analogamente a quanto detto per i vettori, il tensore assoluto è unagrandezza invariante rispetto al sistema di riferimento, ma non sono tali lesue componenti (nè le vettoriali, nè le scalari)

Esempi di tensori sono gli sforzi superficiali, i momenti di inerzia etc..

FLUSSO DI UNA GRANDEZZA ESTENSIVA

Una delle caratteristiche più essenziali (ai fini termodinamici) delle grandezzeestensive è che esse (e solo esse) possono fluire (possono cioè esserescambiate tra il sistema e il suo ambiente).

Si definisce flusso di una grandezza estensiva G in un punto, lagrandezza che dà, in intensità e direzione, la quantità di G che fluisce perunità di superficie e per unità di tempo.

Associata al concetto di flusso è quindi una direzione orientata riconoscibiledalla direzione secondo la quale la grandezza fluisce. Pertanto, se la gran-dezza G è un tensore di ordine k, il flusso di G è un tensore di ordine k + 1.

Esempio: il flusso di massa è un vettore (tensore di ordine uno) essendo lamassa uno scalare (tensore di ordine zero), il flusso di quantità di moto è untensore del secondo ordine essendo la quantità di moto un vettore e così via.

G

FLUSSO DI UNA GRANDEZZA ESTENSIVA

Le dimensioni del flusso sono: tL2

G

ΦG

Nella definizione di flusso è insito il concetto di trasporto di unagrandezza, e quindi di velocità, come può del resto dedursi dalledimensioni stesse del flusso infatti

VgtL

LGΦ +

G

3

[V] dimensioni di una velocità

Il flusso può essere comunque espresso come prodotto della densitàvolumetrica della grandezza G per una opportuna velocità W.

W g ρ = Wg = Φ +G

Il flusso dipende, in generale, dal sistema di riferimento.

FLUSSO DI UNA GRANDEZZA ESTENSIVA

Introducendo la velocità V di una particella elementare (più propriamente lavelocità V del centro di massa di una particella elementare) è possibile effet-tuare una importante scomposizione del flusso di una grandezza estensiva G.

La precedente relazione opera una scomposizione del flusso totale di G,[misurato in un sistema di riferimento galileiano (,,,)] in due parti:

a) un flusso convettivo o macroscopico che risulta pari al prodottodella densità volumetrica ( g) di G per la velocità di massa V della particellaelementare anch'essa misurata nel sistema di riferimento (,,,). Essorappresenta la G che si accompagna alla massa che fluisce;

b) un flusso diffusivo o microscopico che rappresenta la differenzatra il flusso totale e quello macroscopico e che risulta diverso da zero se iltrasporto della grandezza G non è dovuto unicamente al trasporto convettivo(il quale è associato al moto del centro di massa della particella), ma ad unfenomeno di diffusione della grandezza G (pressione, flusso di calore, ecc.).

GG J +Vg ρ= Φ

PRODUZIONE DI UNA GRANDEZZA ESTENSIVA

Una grandezza estensiva, oltre a fluire può, in generale, essere prodotta(in senso algebrico), cioè può essere creata o distrutta (ad es. reazionichimiche)

La produzione di una grandezza estensiva può, ovviamente, variare dapunto a punto del sistema ed, in ogni punto, da istante a istante

Si definisce quindi la produzione di una grandezza estensiva G in unpunto la quantità di G che si crea o si distrugge per unità di volume eper unità di tempo nel punto considerato.

Se la produzione di una grandezza è sempre identicamente nulla, si diceche la stessa si conserva o, equivalente mente, che la grandezza èconservativa

Le dimensioni della produzione sono: tL

Gg+

3

PRODUZIONE DI UNA GRANDEZZA ESTENSIVA

Si può definire anche la produzione di G per unità di massa e unità ditempo che sarà indicata con:

g ρ= g

;

+g v= g

A titolo di esempio, si noti che la produzione della quantità di moto ha ledimensioni:

atL

V

3

(dove con [a] sono state indicate le dimensioni di un'accelerazione) per cuiessa ha le dimensioni di una forza per unità di volume.

Le dimensioni tensoriali della produzione sono le stesse di quelle dellagrandezza G da cui essa è derivata.

;

IL CAMMINO LIBERO MEDIO MOLECOLARE E L'IPOTESI DEL CONTINUO

La materia, pur apparendo macroscopicamente continua, è di fatto costituitada un numero elevatissimo di particelle discrete, che si chiamano molecole.

Nel famoso libro sulla teoria cinetica dei gas, scritto nel 1940, Sir J.Jeans dice:

“Un uomo, ogni volta che inspira o espira, scambia con l'ambiente circa 400cm3

di aria. Come si vedrà poi, ogni singolo respiro contiene circa 1022 molecole. Èstato stimato che tutta l'atmosfera della terra è costituita da circa 1044 molecole.

Quindi, una molecola sta, rispetto al numero di molecole contenute in unrespiro, nello stesso rapporto con il quale queste ultime stanno rispetto alnumero di molecole contenute in tutta l'atmosfera”. 1044 : 1022 = 1022 : 1

Se si suppone che l'ultimo respiro (e cioè, l’espirazione, dopo che è statopugnalato) di Giulio Cesare, al giorno d'oggi (dopo circa 2000 anni), si sia com-pletamente disperso nell'atmosfera, statisticamente un individuo ogni volta cheinspira, immette nei suoi polmoni una molecola di questa sua espirazione.

Inoltre, poiché i nostri polmoni contengono circa 2 litri di aria, verosimilmenteognuno di noi ha nei suoi polmoni circa 5 molecole dell'ultimo respiro diGiulio Cesare!

IL CAMMINO LIBERO MEDIO MOLECOLARE E L'IPOTESI DEL CONTINUO

Un gas, macroscopicamente continuo, è quindi costituito da un elevatis-simo numero di molecole.

Una mole di gas (e cioè una massa di gas in grammi pari al numero cheesprime la massa molecolare del gas) contiene un numero di AvogadroN = 6.023x1023 di molecole (ad es.: 4g di He, 28g di N2, 32g di O2, ecc.).

Una mole di gas, a temperatura e pressione normali (T = 0°C; p = 1ata),occupa circa 22.4litri.

Perciò, a 20°C e p = 1ata, 400cm3 di aria contengono ≈1022 molecole.

Per l'aria in condizioni normali, la distanza tra le molecole è pari a circa10 volte il loro diametro equivalente. = (22.4 x 10 -3/N)1/3 = 3.3 x 10 -9m.

Le molecole si muovono continuamente, piuttosto indipendentemente l'unadall'altra salvo che negli istanti in cui urtano tra loro (nell’aria in condizioninormali, ogni molecola subisce circa 7 miliardi di urti al secondo).

La traiettoria delle molecole tra due urti consecutivi può essereconsiderata abbastanza rettilinea, poiché le forze intermolecolari (tra lemolecole) sono molto deboli salvo che durante gli urti.

IL CAMMINO LIBERO MEDIO MOLECOLARE E L'IPOTESI DEL CONTINUO

Infatti, ciò garantisce che in sia presente un elevato numero dimolecole e che in esista un numero elevato di .

Il cammino libero medio molecolare è definito come la distanzamedia percorsa dalla molecola tra due urti consecutivi.

Poiché gli urti tra le molecole sono quelli mediante i quali essescambiano sia energia, che quantità di moto, il cammino libero mediomolecolare è una grandezza molto importante in fluidodinamica.

Cammino libero medio molecolare

Validità dell’ipotesi di continuità del sistema

Difatti, come si vedrà, per l’aria in condizioni normali = 7.2x10-8m, uncubetto di lato contiene circa 104 molecole, quantità già molto elevata.

L’ipotesi del continuo comporta che nel sistema esista, comunque, unvolumetto molto più piccolo del volume di controllo in esame( ) ma molto più grande del cubo del cammino libero mediomolecolare ( ).

3

STIMA DEL CAMMINO LIBERO MEDIO MOLECOLARE

Infatti, due molecole entrano in collisione quando i loro centri sono a unadistanza inferiore al loro diametro d e cioè quando il centro della molecolaurtata entra nella cosiddetta sezione d’urto di quella presa in considerazione.

La molecola percorrerà nel tempo una traiettoria di lunghezza mediamente pari a .

Il rapporto tra lo spazio percorso ed il numero di urti (numero di molecolecontenute nel volume spazzato) rappresenta il cammino libero medio dellamolecola , qui stimato con l'approssimazione che tutte le altre molecolesiano ferme:

La velocità media di una molecola sia pari a .

Nel percorrere questo spazio la molecola entrerà incollisione con tutte le altre molecole contenute nelvolume da essa spazzato , le quali, se siindica con n il numero di molecole presente per unitàdi volume, risultano pari a .

; a = approssimato

CAMMINO LIBERO MEDIO MOLECOLARE

Una più esatta espressione del cammino libero medio molecolare è laseguente:

n2d

1=

2

Il cammino libero medio molecolare consente di introdurre un numeroadimensionale (in quanto rapporto di due lunghezze), chiamato numero diKnudsen Kn, definito come

LKn /=

REGIMI DI MOTO

Per Kn <10-2, il moto può essere considerato continuo, nel qualcaso la velocità del fluido in prossimità della parete risulta ugualea quella della parete stessa (ipotesi di continuità). Se la parete èferma, anche il fluido è fermo.

Per 10-2 < Kn <10-1, si può continuare a considerare il moto continuonel campo di moto, ma la velocità del fluido alla parete può esserediversa da quella della parete (slip flow).

Per 10-1 < Kn < 3, il regime di moto è detto di transizione. Il regimedi transizione risulta molto complesso da trattare.

Per Kn > 3, si passa al regime di molecole libere. In quest'ultimoregime, gli effetti degli urti tra le molecole e la superficie solida diun corpo sono predominanti rispetto a quelli dovuti agli urti tra lemolecole stesse (modello newtoniano).

Valutazione del cammino libero medio molecolare

d = 3.4 x 10-10m

mean free path

Valutazione del cammino libero medio molecolare

7.2 x 10-8m

LOGICA DEL BILANCIO

Dato un campo di moto di un fluido, le grandezze incognite necessarie acaratterizzarlo sono di due tipi:

termodinamiche

cinematiche

Le incognite fondamentali sono costituite da tutte le grandezze estensive (ad es. la massa , l'energia totale tE , l'entropia S, la quantità di moto V) e

per ciascuna di queste grandezze si può formulare un'equazione del bilancio.

LOGICA DEL BILANCIO

Detta G una qualunque grandezza estensiva, il bilancio di questa grandezza nel sistema può essere espresso mediante una formulazione a blocchi:

Variazione di G in

=

Interazione con

l'ambiente esterno via

D

+

Produzione

per cause interne in

V

Equazione formale del bilancio

LOGICA DEL BILANCIO

Variazione di G in

= Interazione

con l'ambiente esterno via D

Equazione formale della conservazione

Se la grandezza G è conservativa l’equazione del bilancio diventa:

FORMULAZIONE DEL BILANCIO

tdtrtdtrgGt tG= , g ,r = , = VVVV

V V

dgdt

d =

dt

dGt

VVVV

tG = = dgdgG

La portata elementare della grandezza estensiva G cheattraversa dD è data dalla quantità:

dDΦdDΦ = n nGG

) (

dDΦ nGD

Portata totale

GΦ

FORMULAZIONE DEL BILANCIO

V V

VV D G dgdDnΦdg

dt

d

+ =

GsGG JVVgJVg Φ + =

D G

D s

dgdDnJ

dDnVVgdgdt

d

V = +

+ +

V

VV

Se la superficie D del sistema non è fissa rispetto al sistema diriferimento in cui è valutata la V, ma è dotata di una velocità sV

BILANCIO DELL'ENTROPIA PER UN SISTEMA CHIUSO(II PRINCIPIO DELLA TERMODINAMICA)

Per sistemi puramente meccanici (con scambi di energia che avvengonosolo nel modo lavoro) non si scambia anche entropia

Per i sistemi aperti non esiste un modo univoco di definire il flusso dientropia: quando fluisce la massa, fluiscono simultaneamente l'entropia el'energia

Per un sistema chiuso, il flusso di entropia è associato al solo flusso dienergia nel modo calore

Il sistema è chiuso quindi: 0 nVV s

D s dsdDnJ

dt

dS

+ =

V V

BILANCIO DELL'ENTROPIA PER UN SISTEMA CHIUSO(II PRINCIPIO DELLA TERMODINAMICA)

T

J= J q

sRicordando che:

D

q dsdDnT

J

dt

dS

V V + =

dtdsdDnT

JdS

D

q + =

V

V

SSdS ie + =

dtdDn T

JS

D

q

e =

dtdsS i = V V

;

BILANCIO DELL'ENTROPIA PER UN SISTEMA CHIUSO(II PRINCIPIO DELLA TERMODINAMICA)

Trasformazione adiabatica. Se in tutti i punti della superficie del sistema siverifica:

0 = nT

J q 0= Se

Trasformazione reversibile. Si dice reversibile una trasformazione durante laquale si verifica che:

0 =s 0 = Si

Trasformazione isoentropica. Se l'entropia del sistema si mantienecostante durante la trasformazione, questa è detta isoentropica, infatti:

dS = 0 S = cost.

BILANCIO DELL'ENTROPIA PER UN SISTEMA CHIUSO

a) Una trasformazione adiabatica e reversibile è necessariamente anche isoentropica:

Se = Si = 0 dS = 0

b) Una trasformazione isoentropica non è necessariamente adiabatica, e/o reversibile, potendo essere:

dS = 0 con Se = – Si 0

e cioè l'entropia prodotta viene riversata nell'ambiente. c) una trasformazione adiabatica e isoentropica è necessariamente anche reversibile:

Se = dS = 0 Si = 0

d) una trasformazione adiabatica non è necessariamente isoentropica, e/o reversibile, potendo essere:

Se = 0 con dS = Si 0

e cioè la variazione di entropia è dovuta alla sua produzione. e) una trasformazione isoentropica e reversibile è necessariamente anche adiabatica:

Si = dS = 0 Se = 0

f) una trasformazione reversibile non è necessariamente isoentropica, e/o adiabatica, potendo essere:

Si = 0 con dS = Se 0

e cioè la variazione di entropia è dovuta agli scambi con l'ambiente.

Formulazione Euleriana

(sistema a volume costante)

Formulazione Lagragiana

(sistema a massa costante)

RAPPRESENTAZIONE EULERIANA / LAGRANGIANA

Il sistema di riferimento rispetto al quale si scriveranno tutte le equazionisarà in generale inerziale.

RAPPRESENTAZIONE LAGRANGIANA O MATERIALE

La particella nel generico istante di tempo si può rappresentare comefunzione della sua posizione iniziale or e del tempo t:

Scelto un sistema di coordinate rispetto alle quali si intende studiare il motodel fluido, si supponga che le varie particelle di fluido (masse elementari difluido) rimangano distinte sul piano macroscopico nel loro moto.

trrr o ,

Le coordinate che specificano il vettore posizione iniziale or delle particelledi fluido vengono generalmente indicate come coordinate materiali olagrangiane; esse unite alla variabile tempo formano l'insieme dellevariabili indipendenti per la descrizione lagrangiana del moto.

RAPPRESENTAZIONE EULERIANA

Si supponga che la trasformazione inversa di quella lagrangiana esista e cheessa si può scrivere formalmente come:

trrr oo ,=

Le coordinate che specificano il vettore posizione r si chiamano coordinatespaziali o euleriane; esse unite alla variabile tempo formano l'insieme dellevariabili indipendenti per la descrizione euleriana del moto.

DERIVATE SOSTANZIALE E LOCALERISPETTO AL TEMPO

ooo z,y,x

e (x,y,z) sono, nell'ordine, le coordinate materiali di una

particella e le coordinate spaziali di un punto in un sistema di riferimentoche, per semplicità di trattazione, si suppone cartesiano ortogonale

La derivata materiale o sostanziale (lagrangiana) rispetto al tempo di unagenerica grandezza g si indica con Dg /Dt; essa rappresenta la rapidità conla quale varia la grandezza g misurata da un osservatore che si muove acavallo di una particella elementare.

tzyxgtrgg oooo ,,,, ==

tzyxgtrgg ,,,, ==

La derivata spaziale o locale (euleriana) rispetto al tempo di una genericagrandezza g si indica con g/ t; essa rappresenta la rapidità con la qualevaria la grandezza g in un punto fisso rispetto al sistema di coordinate diriferimento.

DERIVATA SOSTANZIALELa variazione nel tempo t della generica grandezza g(x,y,z,t),

relativa alla particella considerata, può essere approssimata dai termini delprimo ordine dello sviluppo in serie di Taylor:

=tz,y,x,gt Δ+tΔz,zΔy,yΔx,xg=g Δ part

z Δz

g +y Δ

y

g x Δ

x

g t Δ

t

g

y,tx,z,tx,z,ty,r

e dividendo per t:

t Δ

z Δ

z

g +

t Δ

y Δ

y

g +

t Δ

x Δ

x

g

t

g =

t Δ

g Δ

part

t 0 wz

g +v

y

g +u

x

g

t

g =

t D

Dg

g Vt

g =

t D

Dg

TEOREMA DEL TRASPORTO

V VVV

0 = = dtrdtr o ,,

La generica grandezza estensiva totale associata ad

= dgG

TEOREMA DEL TRASPORTO

=, , , , = VV0V V

dtrgtrdtrgtrG oo

La variazione di G nell'intervallo di tempo t

o

oo ttttdgdgdgdg VVVV

VVVVV V o0

ott

dgdg

VVVV -VVV -V o

o

o

+

Dividendo per t e passando al limite per t 0

t

G

=/ d

dt

dgDtDG

+

=

o

o

t Δlim

Dt

DG

0 t Δ

ott

dgdg

VVVV VV

t Δlim

0 t Δ

ott

dgdg

VVVV -VVV -V oo

o

+

TEOREMA DEL TRASPORTO

Per t 0 si ha V V V V ed il primo limite delsecondo membro

o

V

V odg

dt

d

t Δlim

0 t Δ

ott

dgdg VVVVVV oo

TEOREMA DEL TRASPORTO

+

=

o

o

t Δlim

Dt

DG

0 t Δ

ott

dgdg

VVVV VV

t Δlim

0 t Δ

ott

dgdg

VVVV -VVV -V oo

o

+

TEOREMA DEL TRASPORTO

La quantità di G che attraversa la superficie dD nel tempo t si puòscrivere tdDnVg dg V

t Δlim

0 t Δ

ott

dgdg VVVV -VVV -V ooo

dDngD

o V

TEOREMA DEL TRASPORTO

dDnVgdgDt

DG

o

o + = Ddt

d VV

VVVV o

dVgdgDt

DG + =

o

dt

d

In definitiva:

e facendo uso del teorema della divergenza: