Corso di Dinamica delle Strutture

Dispense - parte #1

A.A. 2015∼2016

Versione 1.1.2

Indice

1 Grandezze fisiche 31.1 Un Esempio semplice ma non banale . . . . . . . . . . . . . . . . . . . . . . . . . 3

2 Il Modello di Oscillatore Semplice 52.1 Potenza & Lavoro . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62.2 Principio di Bilancio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72.3 Energia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72.4 Potenze & Energie dell’oscillatore . . . . . . . . . . . . . . . . . . . . . . . . . . . 72.5 Principio di Dissipazione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82.6 Principio di Dissipazione per l’Oscillatore . . . . . . . . . . . . . . . . . . . . . . 92.7 Il moto dell’oscillatore . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

3 Oscillatore libero 113.1 ζ = 0: moto armonico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113.2 0 < ζ < 1: moto sotto-smorzato . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133.3 ζ = 1: smorzamento critico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143.4 1 < ζ: moto sovra-smorzato . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143.5 Esempi: la soluzione omogenea . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143.6 Decremento logaritmico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

4 Oscillatore forzato 174.1 Forzante armonica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174.2 Dissipazione. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214.3 Esempio ‘fai da te’ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224.4 Forzante periodica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 234.5 Risposta alla forzante periodica . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

4.5.1 Esempio: onda quadra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274.6 Analisi nel dominio della frequenza . . . . . . . . . . . . . . . . . . . . . . . . . . 294.7 La Funzione Impulso . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314.8 L’Impulso Meccanico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314.9 La Risposta all’Impulso dell’Oscillatore . . . . . . . . . . . . . . . . . . . . . . . 334.10 La Funzione Gradino . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 344.11 La Risposta al Gradino dell’Oscillatore . . . . . . . . . . . . . . . . . . . . . . . . 35

4.11.1 Esempio: gradino rettangolare . . . . . . . . . . . . . . . . . . . . . . . . 36

1

4.12 L’integrale di convoluzione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 364.12.1 Esempio: convoluzione armonica . . . . . . . . . . . . . . . . . . . . . . . 38

4.13 Forzanti notevoli: la mezza-armonica e l’urto . . . . . . . . . . . . . . . . . . . . 384.13.1 Mezza armonica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

z z z

2

1 Grandezze fisiche

La nozione di grandezza fisica e fondamentale; tale nozione non va confusa con quella di unitadi misura. Nel Sistema Internazionale di unita di misura (SI), le grandezze fisiche si dividono insette grandezze base e numerose grandezze derivate. Le sette grandezze fisiche fondamen-tali del Sistema Internazionale, con le relative unita di misura, sono riportate in tabella (1).Nell’ambito di questo corso avremo a che fare essenzialmente con le prime tre grandezze fon-

Simbolo Grandezza fisica Unita di misura Simbolo unita

L lunghezza metro m

M massa kilogrammo kg

T intervallo di tempo secondo s

I intensita di corrente ampere A

Θ temperatura assoluta kelvin K

n quantita di sostanza mole mol

Iv intensita luminosa candela cd

Tabella 1: Le Grandezze Fisiche Fondamentali

damentali (lunghezza, massa e intervallo di tempo) e con alcune grandezza derivate di notevoleimportanza meccanica. Per evitare di scrivere scomode combinazioni di grandezze, introduciamodei simboli per le quattro grandezze derivate di uso piu frequente, vedi tabella (2); il numero1 denota le grandezze adimensionali. Per indicare la grandezza fisica di una data quantita α

Simbolo Grandezza fisica Definizione Unita di misura Simbolo unita

F forza F = M LT−2 newton N

E energia, lavoro E = F L joule J

P potenza P = E T−1 watt W

ϑ angolo ϑ =arco/raggio radiante rad

Tabella 2: Grandezze Fisiche Derivate

useremo la notazione [α]. Ad esempio:

[dv] = Ln volume di un corpo n-dimensionale;

[da] = L(n−1) area di una superficie (n-1)-dimensionale;

[ω] = [rad/s] = 1/T radianti al secondo, ossia, velocita angolare.

(1)

1.1 Un Esempio semplice ma non banale

Sapete la differenza tra forza, lavoro, potenza, energia? Quale di queste nozioni e la piu impor-tante? Quello che probabilmente sapete e che alcune volte si ‘paga la potenza’ (un aspirapolvere

3

potente costa di piu di uno meno potente, cosı come un forno a microonde, oppure una automo-bile); altre volte si ‘paga il lavoro’ (l’energia elettrica, il pieno di benzina). In entrambe i dueultimi casi (energia elettrica, benzina), in realta paghiamo per un qualcosa che saremo poi ingrado di convertire in lavoro.

Prendiamo un esempio piu semplice e piu ‘meccanico’: il signor A. deve raggiungere il quartopiano di un edificio, salendo le scale a piedi, allora:

• l’unica forza in gioco e la forza peso F = mg, dove m e il peso di A. e g = 9.8m/s2

l’accelerazione di gravita;

• indichiamo con h il dislivello da superare; allora, il lavoro necessario sara L = F h;

• indichiamo con T il tempo impiegato per salire le scale; allora, la potenza sviluppata saraP = L/T .

La cosa importante da notare e che il signor A. non arrivera mai alla meta se non sviluppera,istante per istante, una certa potenza P : e la potenza che consente di compiere un lavoro.Possiamo dire che il lavoro e una nozione integrale, in quanto si riferisce ad un intero percorso;la potenza e una nozione istantanea, in quanto considera un solo istante. Riassumendo:

la potenza e la nozione fondamentale della meccanica.

Continuando con il nostro esempio, possiamo aggiungere che:

• il lavoro meccanico viene estratto dal lavoro metabolico con un’efficienza η < 1;

• il lavoro metabolico Lm necessario sara dato da Lm = L/η;

• inoltre, il metabolismo e sensibile alla potenza sviluppata (avete sentito parlare di eserciziaerobici e anaerobici?) e quindi non e cosı semplice calcolare quanti calorie ‘bruciera’ ilsignor A. per fare le sue scale.

E l’energia? L’energia non entra in gioco in questo esempio. Nonostante la parola energia siauna delle parole di origine tecnico-scientifica piu usate da tutti, la maggior parte delle cose cheaccadono sotto i nostri occhi non ha nulla a che fare con l’energia; piuttosto, il fenomeno piuimportane e la dissipazione. Ed infatti, il signor A., riscendendo se scale non riacquistera il lavoroche ha usato per salirle; anzi, dovra spendere altro lavoro per scendere le scale. Ne spenderapero di meno perche in nostri muscoli sono progettati per ‘frenare’ e non per ‘accelerare’: avetenotato che quando tornate dalla montagna impiegate meno tempo di quello che avete dedicatoalla salita? Eppure il lavoro fatto e lo stesso (forza peso x dislivello): il motivo e che le gambesono in grado di erogare una potenza maggiore quando si va in discesa.

4

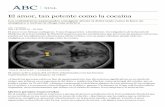
2 Il Modello di Oscillatore Semplice

k

c

m

x

x = 0

fela

f ine

fvisfext

Figura 1: Sinistra: schema classico del modello di oscillatore semplice. Un oggetto di massa m,vincolato a muoversi lungo l’asse orizzontale, e collegato al suolo tramite una molla di rigidezzak ed uno smorzatore di viscosita c. La posizione di tutto l’oggetto viene descritta dalla posizionex di un solo punto; l’origine dell’asse x e preso in corrispondenza della posizione di riposo dellamolla. Destra: schema delle quattro forze agenti sull’oggetto considerato; l’unica forza chepossiamo controllare e quella esterna.

Un oscillatore semplice e un sistema ad un solo grado di liberta, soggetto a forze di varianatura; la configurazione del sistema e descritta dalla funzione x(τ) che associa ad ogni istantedi tempo τ una posizione x sulla retta reale:

T 3 τ 7→ x(τ) ∈ R ; (2)

T = (0, τ1) rappresenta il generico intervallo temporale. Data la descrizione del moto (2),indicheremo con un punto la derivata rispetto al tempo e con una tilde la velocita virtuale:

x , velocita; x , velocita virtuale. (3)

Il moto dell’oscillatore semplice e descritto dalle seguenti tre equazioni

mx(τ) + c x(τ) + k x(τ) = f(τ) , bilancio delle forze, verificato ∀τ ∈ T ;

x(0) = xo , posizione iniziale, verificata per τ = 0;

x(0) = vo , velocita iniziale, verificata per τ = 0.

(4)

dove la massa m, la viscosita c, e la rigidezza k sono tre grandezze scalari positive. L’equazionedi bilancio delle forze puo essere riscritta in modo piu significativo dal punto di vista meccanico,definendo:

Tipo di forza Prescrizione Analisi dimensionale

Forza esterna: fext(τ) = f(τ) , [f ] = F ;

Forza elastica: fela(τ) = −k x(τ) , [x] = L , [k] = F/L ;

Forza viscosa: fvis(τ) = −c x(τ) , [x] = L/T , [c] = F T/L ;

Forza d’inerzia: f ine(τ) = mx(τ) , [x] = L/T 2 , [m] = M ;

(5)

Allora, l’equazione (4)1 si riscrive

f ine(τ) = fela(τ) + fvis(τ) + fext(τ) , ∀τ ∈ T . (6)

5

Notiamo che le ultime tre definizioni di forza che appaiono in (5) rappresentano delle relazionicostitutive, ossia, delle prescrizioni che legano il moto alla forza; ad esempio, la prescrizione perla forza d’inerzia puo essere letta nel seguente modo: prendere il moto x(τ), derivarlo due volterispetto al tempo, e infine moltiplicare il risultato per lo scalare m che rappresenta la massadel sistema. La prescrizione per la forza viscosa fvis ci dice che tale forza e proporzionale allavelocita (con il segno meno); la prescrizione per la forza elastica fela ci dice che tale forza eproporzionale allo spostamento e si oppone ad esso.

Notiamo infine che queste tre forze dipendono linearmente dal moto; per tale motivo lasoluzione del problema (4) si ricava senza problemi, ed il modello di oscillatore viene dettosemplice.

Tali tre forze descrivono in modo dettagliato cosa avviene al punto materiale sotto esame,e non possono essere controllate dallo sperimentatore; per tale motivo due di esse, le forze fela

ed fvis, vengono definite forze interne, dove con l’aggettivo “interne” ci si riferisce al modello,ossia, descritte nell’ambito del modello:

f in = fela + fvis . (7)

L’unica forza su cui possiamo agire per controllare il moto del punto e dunque fext e per talemotivo si usa l’aggettivo “esterna”.

2.1 Potenza & Lavoro

Tra le nozioni fondamentali della meccanica vi e quella di potenza. Tale nozione e una nozioneistantanea, ossia, considera il corpo ad un dato istante, e coinvolge simultaneamente sia il motodel corpo che le forze che agiscono su di esso. Nel caso dell’oscillatore semplice, la potenza edefinita dal prodotto forza per velocita:

P(v(τ)) = f(τ) · v(τ) ,

{v(τ) = x(τ) potenza (effettiva);

v(τ) = x(τ) potenza virtuale.(8)

Osservazione: la notazione P(v(τ)) allude al fatto che la potenza dipende dalla velocita v(τ);per semplificare la notazione scriveremo anche P(v), oppure solo P(τ) per evidenziare la dipen-denza dal tempo. Una volta definita la potenza, possiamo introdurre il lavoro elementare dL(v)compiuto dalla potenza P(v) nell’intervallo di tempo elementare dτ

dL(v) = P(v) dτ = f · v dτ = f · ds , (9)

dove ds = v dτ rappresenta uno spostamento elementare. Il lavoro e una nozione integrale cheprende in considerazione un intervallo finito di tempo:

L(v(τ)) =

∫ τ

0dL(v(t)) =

∫ τ

0P(v(t)) dt =

∫ τ

0f(t) · v(t) dt . (10)

Anche in questo caso possiamo distinguere tra lavoro (effettivo) e lavoro virtuale a seconda chesi integri una potenza od una potenza virtuale. Confrontando le due definizioni precedenti, sinota che la potenza spesa al tempo τ dipende solo da cio che accade a quel tempo; al contrario,il lavoro compiuto al tempo τ dipende da tutto il moto, dall’istante iniziale τ = 0 all’instanteconsiderato τ . Si noti che la (9) equivale a dire che la derivata temporale del lavoro e la potenza

L = P .

6

Data la classificazione delle forze (5), compresa la nozione di forze interne, definiamo le rispettivepotenze:

P ine(v(τ)) = mx(τ) · v(τ) , potenza d’inerzia;

Pvis(v(τ)) = −c x(τ) · v(τ) , potenza viscosa;

Pela(v(τ)) = −k x(τ) · v(τ) , potenza elastica;

P in(v(τ)) = (fela + fvis) · v(τ) , potenza interna;

Pext(v(τ)) = fext · v(τ) , potenza esterna.

(11)

2.2 Principio di Bilancio

L’equazione di bilancio delle forze (6) discende da un principio di bilancio del tutto generale cheviene espresso per il tramite della potenza o del lavoro; in questo secondo caso, prende il nomedi Principio dei Lavori Virtuali. Il principio di bilancio, espresso in termini di potenze, richiedeche:

P ine(x) = P in(x) + Pext(x) , ∀ x velocita virtuale . (12)

E’ semplice verificare che la tale richiesta, dovendo valere per ogni velocita virtuale, equivalealla equazione di bilancio delle forze (6).

2.3 Energia

La potenza e una nozione fondamentale e del tutto generale: ad ogni processo meccanico esempre associata una potenza; al contrario, l’energia e una proprieta peculiare, e solo alcuniprocessi meccanici ammettono un’energia. Un processo e detto energetico se esiste una funzionescalare, detta energia, la cui derivata temporale risulti uguale alla potenza:

d

dτenergia = potenza ; (13)

in tal caso si dice che la potenza puo essere espressa tramite un differenziale esatto. Unendo ladefinizione di energia e la relazione che sussiste tra potenza e lavoro, possiamo scrivere

d

dτenergia = potenza =

d

dτlavoro . (14)

Calcolare il lavoro compiuto durante un’intervallo di tempo diventa molto semplice: non abbiamobisogno di conoscere la legge di evoluzione temporale del moto, ne di svolgere materialmentel’integrale (9), ma basta calcolare la variazione che subisce l’energia tra l’istante iniziale e quellofinale:

Lavoro =

∫ τ1

τ0

potenza dτ =

∫ τ1

τ0

d

dτenergia dτ = energia(τ1)− energia(τ0) . (15)

2.4 Potenze & Energie dell’oscillatore

Possiamo chiederci se le potenze (11) in gioco nel modello di oscillatore ammettano un’energia;la risposta e positiva per la potenza delle forze d’inerzia e di quelle elastiche, mentre e negativa

7

per le forze viscose; per quanto riguarda le forze esterne, la domanda rimane in sospeso finquando tali forze non verranno specificate. Abbiamo:

K(x(τ)) =1

2mx(τ) · x(τ) , energia cinetica;

E(x(τ)) =1

2k x(τ) · x(τ) , energia elastica.

(16)

Osservazione: le notazioni K(x(τ)), E(x(τ)) alludono al fatto che l’energia dipende dal motox(τ) (incluse le sue derivate); per semplificare la notazione scriveremo anche in questo casoK(x), oppure K(τ) per evidenziare la dipendenza dal tempo; lo stesso per E.Osservazione: al contrario della potenza e del lavoro, che possono essere effettivi o virtuali,l’energia considera sempre e solo il moto effettivamente realizzato; si noti ad esempio che nelle(11) compare sia il moto effettivo x(τ) (o le sue derivate) che una generica velocita v(τ), mentrenelle (16) compare solo il moto effettivo (o le sue derivate).Per verificare che le (16) siano delle energie, calcoliamone le derivate rispetto al tempo:

K(x) =1

2mx(τ) · x(τ) +

1

2mx(τ) · x(τ) = mx(τ) · x(τ) = P ine(x) ,

E(x) =1

2k x(τ) · x(τ) +

1

2k x(τ) · x(τ) = k x(τ) · x(τ) = −Pela(x) .

(17)

Dunque, a meno del segno, le due derivate temporali forniscono la potenza effettiva spesa dalleforze d’inerzia ed elastiche.

2.5 Principio di Dissipazione

Il principio di dissipazione dichiara che la variazione temporale di energia cinetica ed interna delsistema e sempre minore od uguale alla potenza spesa dalle forze esterne:

K(x) + E(x) ≤ Pext(x) , qualunque sia il moto realizzato x(τ). (18)

Tale principio ha un significato meccanico immediato: qualunque sia il sistema con cui abbiamoa che fare, e qualunque sia il moto che realizziamo applicando delle forze esterne, una parte dellanostra potenza (la potenza esterna) non sara utilizzata per variare l’energia del sistema.

In termini integrali cio significa che il lavoro esterno fatto durante un intervallo di temponon sara tutto immagazzinato nel sistema sotto forma di energia, ma una parte di esso andraperso. In particolare, in assenza di forze esterne, avremo:

K(x) + E(x) ≤ 0 , qualunque sia il moto realizzato x(τ); (19)

ossia, l’energia immagazzinata nella configurazione iniziale puo al massimo essere conservata(=), altrimenti, diminuira con il tempo (<). Utilizzando il principio di bilancio (12), possiamorappresentare la potenza esterna come differenza tra potenza d’inerzia ed interna, Pext = P ine−P in, e riscrivere il principio di dissipazione nel seguente modo

K(x) + E(x) ≤ P ine(x)− P in(x) , qualunque sia il moto realizzato x(τ). (20)

Inoltre, essendo K(x) = P ine(x), possiamo semplificare ulteriormente la richiesta:

E(x) + P in(x) ≤ 0 , qualunque sia il moto realizzato x(τ). (21)

8

La parte che sarebbe necessaria per verificare l’uguaglianza e detta dissipazione, e puo esseredefinita nel seguente modo:

D = −(E(x) + P in(x)) ;

allora, possiamo riscrivere il principio di dissipazione nel seguente modo:

D + E(x) + P in(x) = 0 , D ≥ 0 , qualunque sia il moto realizzato x(τ). (22)

Osservazione: Il principio di dissipazione nella forma (22) fornisce indicazioni su come sidebbano modellare la dissipazione D e la potenza interna P in: qualunque scelta costitutiva perle due grandezze deve soddisfare il principio. Nella sezione seguente vedremo come la scelta diP in per il modello di oscillatore soddisfi il principio.

2.6 Principio di Dissipazione per l’Oscillatore

Verifichiamo ora che il modello di oscillatore soddisfi il principio (22) (se cio non fosse vero, ilmodello sarebbe sbagliato), e vediamo come e fatta la dissipazione D. Nel nostro caso la potenzadelle azioni interne e la somma di due contributi, uno elastico ed uno viscoso:

D + E(x) + Pela(x) + Pvis(x) = 0 , D ≥ 0 , qualunque sia il moto realizzato x(τ). (23)

Inoltre, essendo E(x) = −Pela(x), e Pvis(x) = −c x · x, possiamo scrivere:

D = −Pvis(x) = c x · x , D ≥ 0 , qualunque sia il moto realizzato x(τ). (24)

Dunque la dissipazione e dovuta alle sole forze viscose, ed il principio e sempre verificato (D ≥ 0)in quanto c > 0 e x · x ≥ 0 (zero solo nel caso di velocita nulla); inoltre, la dissipazione e unacaratteristica del sistema e prescinde dalla presenza di forze esterne. Data la (24), e tenuto contodel principio di bilancio (12), e della nozione di energia (17), possiamo scrivere:

K(x) + E(x) +D = K(x) + E(x)− Pvis(x)

= K(x) + E(x) + Pela(x)− P ine(x) + Pext(x)

= Pext(x) .

(25)

Quest’ultima rappresentazione ci dice che una parte della potenza spesa dalle azioni esternecontribuisce a variare l’energia del sistema, mentre un’altra parte viene dissipata (si ricordi cheD ≥ 0). Nel caso di forze viscose nulle abbiamo c = 0 e dunque D = 0: la (25) dice che la potenzadelle azioni esterne viene tutta impiegata per variare l’energia del sistema; in particolare, se ilsistema e libero, ossia, in assenza di azioni esterne, si scopre che l’energia rimane costante neltempo:

K(x) + E(x) =d

dτ(K(x) + E(x) ) = 0 ⇒ K(x) + E(x) = costante . (26)

Il risultato (26) viene chiamato Principio di Conservazione dell’energia;

2.7 Il moto dell’oscillatore

Il moto dell’oscillatore semplice e descritto dalla funzione x(τ), soluzione del sistema (4) cheriscriviamo per comodita:

mx(τ) + c x(τ) + k x(τ) = fext(τ) , bilancio delle forze, verificato ∀τ ∈ T ;

x(0) = xo , posizione iniziale, verificata in τ = 0;

x(0) = vo , velocita iniziale, verificata in τ = 0.

(27)

9

La soluzione del sistema (27) viene affrontato utilizzando una tecnica piuttosto semplice che quiriassumiamo:

1. L’equazione di bilancio delle forze (27)1 e una equazione lineare che conviene riscrivere informa compatta, mettendo in evidenza l’operatore lineare L che descrive l’equazione:

Lx(τ) = f(τ) , ∀τ ∈ T , con L = md2

dτ2+ c

d

dτ+ k . (28)

2. Si cercano le auto-funzioni dell’operatore lineare, ossia quelle funzioni che vengono tra-sformate in se stesse, a meno di una costante:

Lϕ(τ) = costϕ(τ) , ∀τ ∈ T . (29)

Tutte le funzioni del tipo ϕ(τ) = u exp(λ τ), con u, λ costanti, verificano la (29); inparticolare abbiamo:

Lϕ(τ) = (mλ2 + c λ+ k )ϕ(τ) (30)

3. Le auto-funzioni sono il punto di partenza per costruire le soluzioni dell’equazione omoge-nea, ossia, per risolvere il caso con forzante nulla:

Lx(τ) = 0 , ∀τ ∈ T ⇒ Lϕ(τ) = (mλ2 + c λ+ k )ϕ(τ) = 0 , ∀τ ∈ T . (31)

L’equazione (31) deve essere verificata ad ogni istante; allora, abbiamo due sole possibilita:

soluzione banale con auto-funzione nulla: ϕ(τ) = u exp(λ τ) = 0 ⇔ u = 0 ,

soluzione interessante con auto-funzione non nulla: mλ2 + c λ+ k = 0 .(32)

4. La soluzione generale xg e la somma della soluzione omogenea xom, corrispondente aforzante nulla, e della soluzione particolare xf , che risolve il caso con forzante f :

xg(τ) = xom(τ) + xf (τ).

Inserendo xg nella (28) si ottiene infatti

Lxg = L (xom + xf ) = Lxf = f .

La ricerca della soluzione generale xg = xom+xf va dunque sempre fatta in due passi: la ricercadi xom e di xf . La soluzione omogenea xom e completamente caratterizzata dall’equazionealgebrica di secondo grado (32)2, detta equazione caratteristica, e la sua ricerca viene effettuatauna sola volte per tutte. Al contrario, non esiste una rappresentazione generale per xf , e la suaricerca va fatta caso per caso.

Nel seguito verra mostrato come si caratterizza xom; quindi, descriveremo il moto dell’o-scillatore soggetto a forze esterne, considerando problemi con difficolta crescente: 1) forzantearmonica; 2) forzante periodica; 3) forzante impulsiva; 4) forzante generica.

10

3 Oscillatore libero

Iniziamo considerando il sistema (27) in assenza di forzanti esterne; in questo caso il moto einnescato da condizioni iniziali non nulle. Come detto, la ricerca di soluzioni ci porta a risolverel’equazione caratteristica (32)2: solo alcuni valori di λ sono ammissibili, e il tipo di moto dipendeproprio da tali valori. L’equazione caratteristica viene riscritta nel seguente modo

mλ2 + c λ+ k = 0 ⇒ λ2 +c

mλ+

k

m= 0 ⇒ λ2 + 2 ζ ω λ+ ω2 = 0 , (33)

che evidenzia i due parametri importanti che caratterizzano la risposta del sistema:

ω =

√k

m, pulsazione naturale; ζ =

c

2ωm=

c

2√km

, fattore di smorzamento. (34)

Le soluzioni della equazione caratteristica (33)3, scritte in termini di ζ ed ω sono due, a cuicorrispondono due auto-funzioni:

λ1,2 =(−ζ ±

√ζ2 − 1

)ω ⇒ ϕ1,2(τ) = u1,2 exp(λ1,2 τ) . (35)

La soluzione xom puo allora essere scritta come combinazione lineare delle due auto-funzioni:

xom(τ) = u1 exp(λ1 τ) + u2 exp(λ2 τ) ; (36)

le costanti u1,2, che in generale saranno complesse e coniugate, sono determinate dalle condizioniiniziali. La natura del moto dipende dal valore del termine sotto radice ζ2− 1. Infatti, sia ζ cheω sono numeri reali maggiori od uguali a zero, e le soluzioni λ1,2 possono essere raggruppate in4 casi:

• ζ = 0: le radici sono immaginarie coniugate e il moto e puramente oscillatorio;

• 0 < ζ < 1: le radici sono complesse coniugate; la parte reale da smorzamento, quellaimmaginaria oscillazioni;

• ζ = 1: le radici sono reali e coincidenti; questo caso separa i moti con oscillazioni da quellisenza;

• ζ > 1: le radici sono reali e distinte; il moto e smorzato senza oscillazioni.

3.1 ζ = 0: moto armonico

Il caso piu semplice e quello in cui lo smorzamento e nullo (c = 0 ⇒ ζ = 0); l’equazionecaratteristica fornisce

mλ2 + k = 0 ⇒ λ2 +k

m= 0 ⇒ λ2 + ω2 = 0 , ⇒ λ1,2 = ±i ω . (37)

Abbiamo dunque due radici complesse e coniugate, con parte reale nulla; la soluzione completadel problema omogeneo puo essere scritta come combinazione lineare delle due auto-funzioni:

xom(τ) = u1 exp(i ω τ) + u2 exp(−i ω τ) ; (38)

11

le costanti u1,2, che in generale saranno complesse e coniugate, sono determinate dalle condizioniiniziali. La soluzione (38) ammette altre due rappresentazioni che si ricavano a partire dellafondamentale formula di Eulero

exp(± i α) = cos(α)± i sin(α) , α ∈ R . (39)

Ponendo nella (38) u1,2 = (a ∓ i b)/2, e usando la (39), si ottiene la prima rappresentazionecercata

xom(τ) =a− i b

2[cos(ω τ) + i sin(ω τ) ] +

a+ i b

2[cos(ω τ)− i sin(ω τ) ]

= a cos(ω τ) + b sin(ω τ) .

(40)

La (40) e la soluzione generale del problema omogeneo (27) in assenza di forze viscose: l’ag-gettivo generale si riferisce al fatto che abbiamo risolto solo la prima delle tre equazioni delmodello di oscillatore, senza tener conto delle altre due equazioni che esprimono le condizioniiniziali; l’aggettivo omogeneo, invece, allude al fatto che abbiamo considerato forze esterne nulle.Una seconda rappresentazione della soluzione (38) si ottiene a partire dalla (40), utilizzando laseguente relazione trigonometrica

cos(α− β) = cos(α) cos(β) + sin(α) sin(β) . (41)

La (41) consente di riscrivere la soluzione facendo comparire una sola funzione trigonometrica

xom(τ) = A cos(ω τ − φ) , con A =√a2 + b2 , φ = arctan(b/a) , (42)

e per tale motivo il moto viene detto armonico; quest’ultima rappresentazione e molto utilein quanto mette in evidenza l’ampiezza A e la fase φ del moto. I parametri importanti checaratterizzano il moto armonico sono i seguenti:

ω =

√k

m, pulsazione naturale; T =

2π

ω,periodo; f =

1

T, frequenza. (43)

Il valore delle costanti a e b, ovvero il valore di A e φ, sono determinati dalla condizioni iniziali;allo scopo, conviene usare la rappresentazione (40) che fornisce

xom(0) = a cos(ω 0) + b sin(ω 0) = xo ,

xom(0) = −aω sin(ω 0) + b ω cos(ω 0) = vo .

⇒ a = xo ,

b =voω.

(44)

E’ importante notare che il valore delle costanti si trova risolvendo un problema lineare di dueequazioni in due incognite; tale fatto e del tutto generale, e tipico dei problemi differenzialilineari ordinari. La (44) si riscrive infatti[

cos(ω 0) sin(ω 0)

−ω sin(ω 0) ω cos(ω 0)

] [a

b

]=

[1 0

0 ω

] [a

b

]=

[xo

vo

]. (45)

Dunque, la soluzione del problema omogeneo (27) in assenza di forze viscose si scrive:

xom(τ) = xo cos(ω τ) +voω

sin(ω τ)

= A cos(ω τ − φ) , con A =√x2o + (vo/ω)2 , φ = arctan

(voω xo

).

(46)

12

3.2 0 < ζ < 1: moto sotto-smorzato

In questo caso l’equazione caratteristica (33) ha due radici complesse e coniugate, che convieneriscrivere nel seguente modo

λ1,2 = −ζ ω ± i ωd , con ωd = ω√

1− ζ2 ; (47)

la pulsazione ωd, piu piccola della pulsazione naturale ω, viene detta pulsazione smorzata. Lasoluzione omogenea del problema sotto-smorzato e data da

xom(τ) = exp(−ζω τ) [u1 exp(i ωd τ) + u2 exp(−i ωd τ) ] . (48)

Il termine tra parentesi quadre e del tutto analogo alla soluzione armonica (38); ripetendo quantofatto per quel caso, possiamo riscrivere la (48) come segue

xom(τ) = exp(−ζω τ) [ a cos(ωd τ) + b sin(ωd τ) ]

= A exp(−ζω τ) cos(ωd τ − φ) , con A =√a2 + b2 , φ = arctan

(b

a

).

(49)

La (49) rappresenta un moto oscillatorio di pulsazione ωd e fase φ, la cui ampiezza decadeesponenzialmente con legge A exp(−ζω τ); e immediato verificare le seguenti due proprieta

−A exp(−ζω τ) ≤ xom(τ) ≤ A exp(−ζω τ) , limτ→∞

xom(τ) = 0 , (50)

ossia, le oscillazioni del moto sono comprese tra le due curve ±A exp(−ζω τ), e l’ampiezza tendea zero al passare del tempo. La velocita del moto armonico smorzato si ottiene derivando rispettoal tempo la (49)

xom(τ) = exp(−ζω τ) [ (−a ζ ω + b ωd) cos(ωd τ)− (aωd + b ζ ω) sin(ωd τ) ]

= −A exp(−ζω τ) [ ζ ω cos(ωd τ − φ) + ω sin(ωd τ − φ) ] ;(51)

la velocita si annulla negli istanti τ che verificano la condizione

sin(ωd τ − φ)

cos(ωd τ − φ)= −ζ ⇒ τ =

arctan(−ζ) + φ

ωd. (52)

Le costanti a, b, ovvero, A, φ, che compaiono nella (49) si determinano dalle condizioni iniziali

xom(0) = exp(−ζ ω 0) [ a cos(ω 0) + b sin(ω 0) ] = xo ,

xom(0) = exp(−ζω 0) [ (−a ζ ω + b ωd) cos(ωd 0)− (aωd + b ζ ω) sin(ωd 0) ] = vo ,(53)

ossia, in forma matriciale[1 0

−ζ ω ωd

] [a

b

]=

[xo

vo

]⇒

a = xo ,

b =vo + ζ ω xo

ωd.

(54)

13

3.3 ζ = 1: smorzamento critico

Questo caso si verifica quando la viscosita c assume un valore, detto critico, pari a ccr = 2mω =2√km; l’equazione caratteristica (33) ha due radici reali coincidenti

λ1,2 = −ω . (55)

La soluzione omogenea del problema con smorzamento critico e data da

xom(τ) = exp(−ω τ) [ a+ b τ ] . (56)

La (56) rappresenta un moto che avviene senza oscillazioni, la cui ampiezza decade esponen-zialmente con legge τ exp(−ζω τ), e con velocita xom(τ) = exp(−ω τ) [−aω + b (1 − ω τ) ]. Lecostanti a, b si determinano al solito dalle condizioni iniziali; in forma matriciale abbiamo[

1 0

−ω 1

] [a

b

]=

[xo

vo

]⇒

{a = xo ,

b = vo + ω xo .(57)

Il caso ζ = 1 segnala il confine tra i moti oscillatori e quelli senza oscillazioni; il moto consmorzamento critico e quello che, a parita di condizioni iniziali, tende piu velocemente allaposizione stazionaria.

3.4 1 < ζ: moto sovra-smorzato

In questo caso l’equazione caratteristica (33) ha due radici reali e distinte che conviene riscriverenel seguente modo

λ1,2 = −ζ ω ± ωd , con ωd = ω√ζ2 − 1 ; (58)

La soluzione omogenea del problema sovra-smorzato e data da

xom(τ) = exp(−ζω τ) [ a exp(ωd τ) + b exp(−ωd τ) ] . (59)

La (59) rappresenta un moto che avviene senza oscillazioni, la cui ampiezza decade esponenzial-mente; come al solito, le costanti a, b si determinano dalle condizioni iniziali.

3.5 Esempi: la soluzione omogenea

Consideriamo il sistema (27) non forzato, e cerchiamo la soluzione omogenea nei 4 casi esaminati,assumendo come condizioni iniziali xo = 0, xo = vo > 0; abbiamo

ζ = 0) xom(τ) =voω

sin(ω τ) ,

0 < ζ < 1) xom(τ) =voωd

exp(−ζ ω τ) sin(ωd τ) , ωd = ω√

1− ζ2 ,

ζ = 1) xom(τ) = vo τ exp(−ω τ) ,

1 < ζ) xom(τ) =voωd

exp(−ζ ω τ) sinh(ωd τ) , ωd = ω√ζ2 − 1 .

(60)

Si ricordi che sinh(α) = [exp(α)− exp(−α)]/2. Alcuni esempi sono disegnati nelle figure 2 e 3.

14

0 1 2 3 4

−0.4

−0.2

0

0.2

0.4

τ

xom

ζ = 0ζ = 0.2ζ = 1ζ = 1.5

0 2 4 6 8 10

0

0.2

0.4

τ

xom

ζ = 3ζ = 2ζ = 1.1

Figura 2: Andamento nel tempo delle soluzioni (60) (sinistra), e del solo caso sovrasmorzato(destra), per diversi valori di ζ e con vo = 1, ω = 3.

0 2 4 6 8 10−0.4

−0.2

0

0.2

0.4

τ

xom

± vo exp(−ζ ω τ)

xom(τ)

Figura 3: Andamento nel tempo della soluzione sotto-smorzata (60)2 racchiusa dall’inviluppo± vo exp(−ζ ω τ); ζ = 0.2, vo = 1, ω = 3.

3.6 Decremento logaritmico

Il coefficiente di smorzamento ζ puo essere stimato sperimentalmente misurando due ampiezzexom(τ) e xom(τ + T ) in due istanti separati tra loro da un periodo T ; dalla (49) segue infatti:

xom(τ)

xom(τ + T )=

exp(−ζ ω τ) cos(ωd τ − φ)

exp[−ζ ω (τ + T )] cos[ωd (τ + T )− φ]. (61)

Ponendo T pari al periodo di un ciclo, T = 2π/ωd, abbiamo

cos[ωd (τ + Td)− φ] = cos(ωd τ − φ+ ωd T ) = cos(ωd τ − φ+ 2π) = cos(ωd τ − φ) ; (62)

dunque, possiamo scrivere il rapporto xom(τ)/xom(τ + T ) nel seguente modo

xom(τ)

xom(τ + T )=

exp(−ζ ω τ)

exp[−ζ ω (τ + T )]= exp(ζ ω T ) . (63)

Infine, ricordando che T = 2π/ωd = 2π/(ω√

1− ζ2) si scopre che l’argomento dell’esponenzialesi riscrive in funzione della sola incognita ζ. Si definisce decremento logaritmico il logaritmo del

15

rapporto xom(τ)/xom(τ + T ), ossia

δ = log

(xom(τ)

xom(τ + T )

)= ζ ω T =

2π ζ√1− ζ2

. (64)

Per determinare il valore dello smorzamento e sufficiente misurare le ampiezze del moto in dueistanti qualsiasi separati dall’intervallo T , calcolare il logaritmo del loro rapporto e ottenere ζdalla (64)

ζ =δ√

(2π)2 + δ2=

δ

2π+O(δ2) . (65)

Nel caso di smorzamento molto piccolo, si ottiene una stima piu attendibile misurando dueampiezze del moto in due istanti qualsiasi separati da un’intervallo multiplo del periodo, adesempio nT ; abbiamo allora

xom(τ)

xom(τ + nT )= exp(n ζ ω T ) , (66)

ed il decremento logaritmico δ e dato da

δ =1

nlog

(xom(τ)

xom(τ + nT )

). (67)

Ad esempio, sapendo che l’ampiezza di un moto e diminuita del 50% dopo 5 oscillazioni, possiamocalcolare

δ =1

5log

(xom(τ)

xom(τ + nT )

)=

1

5log

(xom(τ)

0.5xom(τ)

)=

1

5log 2 = 0.1386 , (68)

da cui, usando l’approsimazione lineare, si ottiene

ζ ' δ

2π=

0.1386

2π= 0.0221 . (69)

0 1 2 3 4 5 6−0.4

−0.2

0

0.2

0.4

τ

xomx(τ) x(τ + T )

T = 2π/ωd

Figura 4: Misurando l’ampiezza dell’oscillazione in due istanti separati dall’intervallo T = 2π/ωde possibile calcolare il coefficiente di smorzamento ζ.

16

4 Oscillatore forzato

Ci occupiamo ora di descrivere il moto dell’oscillatore soggetto a forze esterne, considerando pro-blemi con difficolta crescente: 1) forzante armonica; 2) forzante periodica; 3) forzante impulsiva;4) forzante generica. Riscriviamo qui per comodita il problema da risolvere

mx(τ) + c x(τ) + k x(τ) = fext(τ) , bilancio delle forze, verificato ∀τ ∈ T ;

x(0) = xo , posizione iniziale, verificata in τ = 0;

x(0) = vo , velocita iniziale, verificata in τ = 0.

(70)

Come gia detto, la risposta generale xg di un sistema forzato e data dalla somma della soluzioneomogenea xom, corrispondente a forzante nulla, e della soluzione particolare xf , che risolve ilcaso con forzante f :

xg(τ) = xom(τ) + xf (τ).

Inserendo la funzione xg nel sistema (70), si ottiene

mxf (τ) + c xf (τ) + k xf (τ) = fext(τ) , bilancio delle forze, verificato ∀τ ∈ T ;

xom(0) + xf (0) = xo , posizione iniziale, verificata in τ = 0;

xom(0) + xf (0) = vo , velocita iniziale, verificata in τ = 0.

(71)

Dunque, la soluzione dell’omogenea xom scompare dall’equazione differenziale, ma rimane nellecondizioni iniziali: le costanti di integrazione a, b dell’omogenea, vedi (40), vanno trovate tenendoconto anche della soluzione particolare xf .

4.1 Forzante armonica

Consideriamo una forza esterna del tipo

fext(τ) = k A cos(α τ) . (72)

La costante A ha le dimensioni fisiche di una lunghezza; tale rappresentazione risultera utile nelseguito in quanto A e l’ampiezza dello spostamento che provoca la forza stazionaria fext(τ) =k A. Data la (72), possiamo riscrivere l’equazione del moto (71)1 dividendo tutti i termini perla massa m, ottenendo

xf (τ) + 2 ζ ω xf (τ) + ω2 xf (τ) = ω2A cos(α τ) . (73)

Si suppone che la soluzione particolare xf sia una funzione armonica avente la stessa pulsazioneα della forzante:

xf (τ) = a cos(α τ) + b sin(α τ) (74)

Inserendo la (74) nell’equazione del moto si ottiene

(ω2 − α2) [a cos(α τ) + b sin(α τ)] + 2 ζ ω α [b cos(α τ)− a sin(α τ)] = ω2A cos(α τ) . (75)

Eguagliando i coefficienti delle funzioni seno e coseno si ottiene un sistema lineare che permettedi determinare le costanti a e b[

ω2 − α2 2 ζ ω α

−2 ζ ω α ω2 − α2

] [a

b

]=

[ω2A

0

]. (76)

17

Risolvendo il sistema, abbiamo

a = A1− (α/ω)2

(1− (α/ω)2)2 + (2 ζ α/ω)2, b = A

2 ζ α/ω

(1− (α/ω)2)2 + (2 ζ α/ω)2. (77)

Il valore delle costanti a, b dipende sia dalle caratteristiche del sistema ω, ζ, sia dalla pulsazionedella forzante α; in particolare, il rapporto β = α/ω ha un ruolo molto importante. L’ampiezzaX e la fase φ del moto xf vengono dunque rappresentate come funzioni di ζ e β:

X(ζ, β) = (a2 + b2)1/2 =A

[ (1− β2)2 + (2 ζ β)2 ]1/2,

φ1(ζ, β) = arctan

(b

a

)= arctan

(2 ζ β

1− β2

),

(78)

e la soluzione particolare (74) si riscrive

xf (τ) = X(ζ, β) cos[α τ − φ1(ζ, β) ] . (79)

Considerando una forza esterna del tipo

fext(τ) = k A sin(α τ) , (80)

e possibile ripetere tutta la procedura appena vista ed ottenere

a = A−2 ζ α/ω

(1− (α/ω)2)2 + (2 ζ α/ω)2, b = A

1− (α/ω)2

(1− (α/ω)2)2 + (2 ζ α/ω)2; (81)

dunque, l’ampiezza X(ζ, β) del moto rimane la stessa, mentre la fase sara data da

φ2(ζ, β) = π + arctan

(b

a

)= π + arctan

(1− β2

−2 ζ β

). (82)

In questo caso, per mettere in evidenza lo sfasamento, conviene rappresentare la soluzioneparticolare per il tramite della funzione seno; ripartendo dalla (74), si ottiene

xf (τ) = X(ζ, β) cos[α τ − φ2(ζ, β) ] = X(ζ, β) sin[α τ − φ3(ζ, β) ] , (83)

con

φ3(ζ, β) = π/2 + arctan

(1− β2

−2 ζ β

). (84)

Esaminiamo ora cosa accade nei casi estremi di pulsazione nulla, α = 0, corrispondente ad unaforzante stazionaria, e di pulsazione che tende all’infinito, α =→∞, ossia, forzante estremamenteveloce; dalla (83) abbiamo1 :

α = 0 ⇒ β = 0 ⇒ X = A , φ2 → 0 ⇒ xf (τ) = A = cost ,

α =→∞ ⇒ β =→∞ ⇒ X → 0 , φ3 → π ⇒ xf (τ)→ 0 .(85)

1Si ricordi che

limβ→0

arctan

(1− β2

−2 ζ β

)= −π

18

Dunque, la costante A che abbiamo introdotto nella (72) rappresenta lo spostamento xf (τ)prodotto da una forza esterna costante nel tempo; inoltre, anche una forzante molto veloceproduce uno spostamento che tende a quello stazionario (addirittura nullo), ma in opposizionedi fase. Per tale motivo viene definito il rapporto G = X/A, detto fattore di amplificazione, chequantifica gli effetti dovuti ad una forzante armonica rispetto ad una forza di pari intensita, mastazionaria

G(ζ, β) =X(ζ, β)

A=

1

[ (1− β2)2 + (2 ζ β)2 ]1/2. (86)

Possiamo riassumere quanto detto con il seguente prospetto:

IN: OUT:

fext(τ) = k A cos(α τ) ⇒ xg(τ) = xom(τ) +G(ζ, β)A cos[α τ − φ1(ζ, β)] ,

fext(τ) = k A sin(α τ) ⇒ xg(τ) = xom(τ) +G(ζ, β)A sin[α τ − φ3(ζ, β)] .

(87)

0 1 2 30

1

2

4

6

β

Gf = k Aζ = 0ζ = 0.1ζ = 0.2ζ = 0.4ζ = 1

0 1 2 30

π/2

π

β

φ3

ζ = 0ζ = 0.1ζ = 0.2ζ = 0.4ζ = 1

Figura 5: Andamento del fattore di amplificazione G(ζ, β) (sinistra) e della fase φ3(ζ, β) (destra)al variare del rapporto β, per diversi valori dello smorzamento ζ.

Gli aspetti importanti della risposta di un oscillatore semplice con forzante armonica sono coltidalle seguenti nozioni:Pulsazione neutra. La pulsazione α cui corrisponde un fattore di amplificazione unitario vienedetta pulsazione neutra; il corrispondente valore di β viene indicato con βn:

G(ζ, β) = 1 ⇒ βn =√

2√

1− 2 ζ2 . (88)

Per ζ = 0 abbiamo βn =√

2; per ζ > 1/√

2 abbiamo sempre G(ζ, β) < 1 tranne che in β = 0.Pulsazione di risonanza. La pulsazione α che rende massimo il fattore di amplificazioneviene detta pulsazione di risonanza ed indicata con αr; il corrispondente valore di β viene dettorapporto di risonanza ed indicato con βr = αr/ω. Il valore βr che rende massima la rispostadipende dal coefficiente di smorzamento ζ e si trova cercando gli zeri della derivata di G(ζ, β)rispetto a β; :

∂

∂βG(ζ, β) = 0 ⇒ βr =

√1− 2 ζ2 . (89)

19

Fattore di qualita. Il valore massimo del fattore di amplificazione viene detto fattore di qualitaed indicato con la lettera Q; tale massimo dipende ovviamente da ζ

Q(ζ) = G(ζ, βr) =1√

4 ζ4 + 4 ζ2 (1− 2 ζ2)=

1

2 ζ+ 0(ζ) = G(ζ, 1) + 0(ζ) . (90)

L’ultima eguaglianza indica che, per piccoli smorzamenti, il massimo si ha in prossimita di β = 1.Per ζ = 0 la risonanza si verifica quando βr = 1, ossia αr = ω, e comporta una amplificazioneinfinita; per ζ > 1/

√2 la risposta non ha piu massimi (Q < 1).

Pulsazioni di mezza potenza. I due valori βi in cui si verifica G(ζ, βi) = Q(ζ)/√

2 sono dettipunti di meta potenza

G(ζ, βi) =Q(ζ)√

2⇒ βi =

(1− 2 ζ2 ± 2

√ζ2 − ζ4

)1/2. (91)

Tale definizione discende dal fatto che la potenza assorbita dallo smorzatore e proporzionaleal quadrato dell’ampiezza: allora, quando la forzante ha pulsazione αi = βi ω, lo smorzatoredissipa meta potenza rispetto al massimo che si verifica per αr.Banda passante. L’intervallo compreso tra i due punti βi e detto banda passante: per valoridella pulsazione α1 ≤ α ≤ α2, avremo G > Q/

√2. Abbiamo dalla (91)

β2 − β1 = 2 ζ + 2 ζ2 + o(ζ4) . (92)

Si noti che questa nomenclatura ha origine nelle applicazioni elettriche e non meccaniche, dovel’obiettivo e spesso quello di amplificare e non di smorzare. La Fig.15 riassume tutte questenozioni per il caso specifico ζ = 0.3.

20

0 β1 βr 1 β2 1/√

2 2 30

1

Q/√

2

Q

2

3

β

Gζ = 0ζ = 0.3

ζ = 1/√

2ζ = 1

Banda passante

Figura 6: Andamento del fattore di amplificazione G(ζ, β) al variare del rapporto β, per alcunivalori di ζ. La curva G(0.3, β) (blu) raggiunge il massimo valore Q, indicato con un cerchio,quando βr = 0.9055; si noti che per β compreso tra β1 e β2, tale curva e sempre maggiore diQ/√

2; la fascia colorata verticale rappresenta dunque la banda passante. La curva G(1/√

2, β)(rosso) decresce in modo monotono a partire da β = 0.

Esempi ζ = 0: moto armonico. In questo caso abbiamo

G(0, β) =1

1− β2; φ(0, β) = 0 per β < 1 , φ(0, β) = π per β > 1 . (93)

Quindi, la soluzione particolare e in fase per β < 1 e in opposizione di fase per β > 1; quandoα 6= ω, ossia β 6= 1, possiamo usare la (79) che fornisce

fext(τ) = k A cos(α τ) ⇒ xg(τ) = xom(τ) +A

1− β2cos[α τ − φ1(0, β)] (94)

La risonanza si ha per α = ω, e l’amplificazione diventa infinita; in questo caso la formulaprecedente non ha piu valore e la soluzione particolare e data da una oscillazione armonica lacui ampiezza cresce linearmente con il tempo:

fext(τ) = k A cos(ω τ) ⇒ xg(τ) = xom(τ) +A

2ω τ sin(ω τ) (95)

4.2 Dissipazione.

Utilizziamo quanto imparato nella sezione (2.6) per calcolare potenza e lavoro dissipati in unsistema sotto-smorzato (0 < ζ < 1), sottoposto ad una forzante armonica fext(τ) = k A cos(α τ).La soluzione omogenea decade con il tempo; esaurito questo contributo, il sistema si muovera aregime con legge xf e velocita xf

xf (τ) = G(ζ, β)A cos(α τ − φ1) , xf (τ) = −αG(ζ, β)A sin[α τ − φ1(ζ, β)] . (96)

21

Calcoliamo ora la potenza dissipata D = −Pvis = c xf · xf e la potenza esterna immessa nelsistema Pext = f · xf ; utilizzando la (96), possiamo scrivere

Potenza dissipata = D(xf (τ)) = c (GA)2 α2 sin2(α τ − φ1) ,

Potenza Esterna = Pext(xf (τ)) = −k A2Gα cos(α τ) sin(α τ − φ1) .

(97)

Dalla precedente espressione si vede che la potenza dissipata dipende dal quadrato dell’ampiezzadel moto X = GA; inoltre, per il tramite di G, dipende da ζ e β:

Dmax = cG2(ζ, βr)A2 α2 sin2(α τ − φ1) = cQ2(ζ)A2 α2 sin2(α τ − φ1) . (98)

Nei punti di meta potenza abbiamo

Dmax/2 = cG2(ζ, βi)A2 α2 sin2(α τ − φ1) =

1

2Dmax . (99)

Il lavoro compiuto in un ciclo si ottiene integrando la potenza tra zero e Ta = 2π/α

Ld =

∫ Ta

0D(τ) dτ = c α π (AG)2 , (100)

Lext =

∫ Ta

0Pext(τ) dτ = −k π A2G sinφ1 . (101)

Per confrontare le due espressioni occorre eliminare k e sinφ1 da Lext; dalla (78) otteniamo

G =1

[ (1− β2)2 + (2 ζ β)2 ]1/2=

1

2 ζ β

[(1− β2

2 ζ β

)2

+ 1

]1/2=

sinφ1

2 ζ β, (102)

mentre dalla (34) si ha k = mω2; utilizzando queste relazioni si ottiene

Lext = −k π A2G sinφ1 = −c α π (AG)2 = −Ld . (103)

ossia, tutto il lavoro esterno fatto sul sistema viene dissipato dallo smorzatore.

4.3 Esempio ‘fai da te’

Il modo migliore per comprendere il significato del fattore di amplificazione e fare un sempliceesperimento utilizzando le proprie mani ed un pendolo (un filo con un peso attaccato in basso).Prendiamo un pendolo di massa m e lunghezza L e sottoponiamo il punto di sospensione ad unospostamento armonico orizzontale η(τ) = ηo sin(α τ), ad esempio, muovendo la nostra manoa destra e sinistra; in conseguenza di cio, il pendolo assumera un moto oscillatorio e la massasubira uno spostamento x(τ) rispetto la posizione di riposo. Sia θ l’angolo formato dal filorispetto la verticale, T la tensione nel filo, mg la forza peso verticale; assumendo oscillazionipiccole, possiamo dire che la tensione nel filo T e circa pari a mg, mentre la sua componenteorizzontale vale circa mg sinθ, vedi Fig.(7)

mg = T cos θ ' T , T sin θ ' mg sin θ , sin θ ' x− ηL

. (104)

22

L’equazione di bilancio relativa al moto orizzontale, considerando anche una forza viscosa, siscrive

mx(τ) + c x(τ) +mg sin θ(τ) = 0 ⇒ mx(τ) + c x(τ) +mg

Lx(τ) =

mg

Lη(τ) ; (105)

ossia, dividendo tutto per m e ricordando che η = ηo sin(α τ)

x(τ) + 2ω ζ x(τ) + ω2 x(τ) = ω2 ηo sin(α τ) , ω =

√g

L. (106)

La precedente equazione e analoga alla (73): il moto del supporto η(τ) ha lo stesso effetto diuna forzante. Per tale motivo valgono gli stessi risultati della (85) che conviene ripetere qui conqualche commento:

La mano si sposta:

lentamente: α = 0 , ⇒ X = A , φ3 = 0 ⇒ il pendolo si sposta insieme alla mano;

velocemente: α =→∞ ⇒ X → 0 , φ3 → π ⇒ il pendolo rimane fermo;

alla risonanza: α = ω ⇒ X →→∞ , φ3 →π

2⇒ il pendolo oscilla molto.

(107)Dunque, muovendo la mano con il periodo giusto e possibile innescare nel pendolo oscillazionimolto ampie anche se la mano si muove pochissimo; se il filo e lungo un metro, la risonanzadovrebbe avvenire con un periodo T = 2π/ω ' 6.28/

√9.8 ' 2 s.

4.4 Forzante periodica

Consideriamo una forza esterna periodica di periodo Ta, ossia, tale che

f(τ + Ta) = f(τ) . (108)

L’insieme delle funzioni periodiche di egual periodo, corredato delle operazioni di somma trafunzioni e di prodotto tra una funzione ed uno scalare, e uno spazio lineare:

F = {f : R→ R, tali che f(τ + Ta) = f(τ)} , insieme delle funzioni periodiche ;

f(τ) , g(τ) ∈ F ⇒ f(τ) + g(τ) ∈ F , somma di funzioni ;

α ∈ R , f(τ) ∈ F ⇒ α f(τ) ∈ F , prodotto funzione per uno scalare .

(109)

In questo spazio lineare introduciamo anche la seguente operazione di prodotto interno o prodottoscalare che associa a due funzioni uno scalare:

f(τ) · g(τ) =2

Ta

∫ τ+Ta

τf(s) g(s) ds . (110)

Il prodotto scalare permette di definire il modulo di una funzione e di misurare la distanza tradue funzioni

‖f(τ)‖ = ( f(τ) · f(τ) )1/2 , modulo di una funzione ;

d(f(τ) , g(τ)) = ‖f(τ)− g(τ)‖ , distanza tra due funzioni .(111)

23

η

L

T

mg

L sin θ

θ

T T cos θ

mg

T sin θ

x

Figura 7: A sinistra vediamo il pendolo in condizioni di riposo, mentre a destra vediamo unagenerica configurazione assunta durante il moto, inclinata dell’angolo θ rispetto la verticale. Idue parametri η e x misurano gli spostamenti orizzontali del punto di sospensione e della massaposta in basso, rispettivamente. L’ipotesi di piccoli spostamenti comporta L sin θ = x − η,cos θ = 1.

Lo spazio delle funzioni periodiche di periodo Ta e dotato di una base costituita da una fun-zione costante e dalle funzione armoniche seno e coseno aventi pulsazione multipla di quellafondamentale α = 2π/Ta

Base: { 1, cos(j α τ), sin(j α τ) } , con j = 1, 2, . . . , α =2π

Ta. (112)

Per semplificare la notazione, definiamo αj = j α, con j = 1, 2, . . . le pulsazioni multiple diα; α1 = α e detta pulsazione fondamentale, mentre tutte le altre sono chiamate pulsazionisuperiori. Si noti che le funzioni armoniche vengono ordinate secondo la pulsazione; cos(α1 τ)e sin(α1 τ) sono chiamate armoniche fondamentali, le altre armoniche superiori. Si noti ancheche gli elementi della base sono tutti ortogonali tra loro: infatti, per ogni i, j, abbiamo

1 · cos(αj τ) =2

Ta

∫ τ+Ta

τcos(αj s) ds = 0 ,

1 · sin(αj τ) =2

Ta

∫ τ+Ta

τsin(αj s) ds = 0 ,

sin(αj τ) · cos(αi τ) =2

Ta

∫ τ+Ta

τsin(αj s) cos(αi s) ds = 0 ; (113)

24

inoltre, le funzioni armoniche hanno modulo uno:

‖ cos(αj τ)‖2 =2

Ta

∫ τ+Ta

τcos2(αj s) ds = 1 ,

‖ sin(αj τ)‖2 =2

Ta

∫ τ+Ta

τsin2(αj s) ds = 1 , (114)

(115)

Ogni funzione periodica di periodo Ta puo essere rappresentata come combinazione lineare dielementi della base, detta sviluppo di Fourier

f(τ) = ao1

2+

∞∑j=1

[ aj cos(αj τ) + bj sin(αj τ) ] ; (116)

l’insieme delle costanti ao, aj , bj , con j = 1, 2, . . . viene detto spettro della funzione f , e caratte-rizza completamente una funzione periodica di periodo Ta e pulsazione fondamentale α = 2π/Ta;ogni costante ha le dimensioni fisiche di una forza. Lo spettro di una funzione e costituito dallecomponenti della funzione data rispetto alle funzioni della base, e si trova proiettando la funzionesulla base

ao = f(τ) · 1 =2

Ta

∫ τ+Ta

τf(s) ds ,

aj = f(τ) · cos(αj τ) =2

Ta

∫ τ+Ta

τf(s) cos(j α s) ds ,

bj = f(τ) · sin(αj τ) =2

Ta

∫ τ+Ta

τf(s) sin(j α s) ds . (117)

Notiamo infine che il primo termine della serie rappresenta il valor medio f della funzione f(τ)

f =1

Ta

∫ τ+Ta

τf(s) ds . (118)

Infatti, il prodotto scalare di f(τ) per la funzione costante 1 fornisce

f(τ) · 1 =2

Ta

∫ τ+Ta

τf(s) ds = 2 f =

2

Ta

∫ τ+Ta

τ( ao

1

2+∞∑j=1

[ . . . ] ) ds = ao ⇒ f =ao2.

(119)Ricordiamo che una funzione viene detta pari o dispari a seconda che un cambio si segnodell’argomento provochi o meno un cambio di segno del valore della funzione:

pari: f(τ) = f(−τ) ; dispari: f(τ) = −f(−τ) . (120)

L’importanza di tale classificazione risiede nel fatto che, rispetto al prodotto scalare scelto,le funzioni pari e dispari sono ortogonali tra loro; indichiamo con p(τ) e d(τ) due funzioni

25

rispettivamente pari e dispari: allora, centrando gli estremi di integrazione nell’origine, possiamoscrivere

p(τ) · d(τ) =2

Ta

∫ Ta/2

−Ta/2p(s) d(s) ds =

2

Ta

(∫ 0

−Ta/2p(s) d(s) ds+

∫ Ta/2

0p(s) d(s) ds

). (121)

Utilizzando le proprieta dell’integrale e delle funzioni pari e dispari, il primo addendo nel terminedi destra puo essere trasformato come segue∫ 0

−Ta/2p(s) d(s) ds =

∫ 0

Ta/2p(−s) d(−s) (−ds) =

∫ Ta/2

0p(−s) d(−s) ds = −

∫ Ta/2

0p(s) d(s) ds ,

(122)Usando questo risultato nella (121) si ottiene quanto detto

p(τ) · d(τ) =2

Ta

∫ Ta/2

−Ta/2p(s) d(s) ds =

2

Ta

(−∫ Ta/2

0p(s) d(s) ds+

∫ Ta/2

0p(s) d(s) ds

)= 0 .

(123)Data l’ortogonalita tra funzioni pari e dispari, la rappresentazione (116) di una funzione pariconterra solo armoniche pari, e dunque bj = 0 per ogni j; analogamente, per una funzione dispariavremo aj = 0.

4.5 Risposta alla forzante periodica

A questo punto, determinare la risposta dell’oscillatore ad una forzante periodica e piuttostosemplice; le considerazioni importanti da fare sono tre:

1. conosciamo la risposta in caso di forzante armonica, vedi (87);

2. una funzione periodica si rappresenta come somma di una costante piu le varie armoniche,vedi la (116);

3. il sistema e lineare.

Dunque, la risposta ad una forzante periodica di periodo Ta = 2π/α sara data da

xf (τ) =1

k

ao1

2+

∞∑j=1

Gj [ aj cos(αj τ − φ1j) + bj sin(αj τ − φ3j) ]

; (124)

dove

Gj = G(ζ, βj) , φ1j = φ1(ζ, βj) , φ3j = φ3(ζ, βj) , βj =j α

ω, (125)

sono il fattore di amplificazione e la fase relativi ad ogni singola armonica. La (124) mostra cheuna armonica, anche di piccola ampiezza ma avente una pulsazione simile a quella di risonanza,βj ' βr, ha un effetto sulla risposta molto grande. Questo aspetto e molto importante soprat-tutto per un oscillatore con smorzamento piccolo o nullo, e quindi con fattore di qualita grandeo infinito: una forzante con una piccola armonica vicino alla risonanza provoca risposte enormi.

26

4.5.1 Esempio: onda quadra

Consideriamo la funzione periodica onda quadra, di periodo Ta e ampiezza 2A, centrata nell’o-rigine; tale funzione e definita dalla richiesta

f(τ) =

. . .

−A per Ta/2 < τ < Ta ,

A per 0 < τ < Ta/2 ,

−A per − Ta/2 < τ < 0 ,

A per − Ta < τ < −Ta/2

. . .

(126)

Un esempio di onda quadra e mostrato nella Fig.(8) per il caso A = 1, Ta = 2; si noti che talefunzione e costante a tratti, e non e definita nei punti ±i Ta/2; inoltre, e una funzione dispari edunque il suo sviluppo di Fourier conterra solo le armoniche dispari, ossia, ai = 0.

�4 �2 2 4

�1.0

�0.5

0.5

1.0

�4 �2 2 4

�1.0

�0.5

0.5

1.0

Figura 8: Sopra: grafico della funzione onda quadra, con A = 1 e Ta = 2; tale funzione e costantea tratti e non e definita nei punti ±i Ta/2. Sotto: grafico dell’onda quadra con sovrapposta lasua rappresentazione di Fourier contenente solo le tre armoniche di ampiezze b1, b3, b5.

Il calcolo dei coefficienti bi fornisce

bi = f(τ) · sin(i α τ) =2

Ta

∫ τ+Ta

τf(s) sin(i α s) ds = −2 [−1 + (−1)i]A

iπ=

4A

iπ, i dispari,

0 , i pari.(127)

e dunque lo spettro dell’onda quadra contiene solo le costanti bi con i dispari; il suo sviluppo diFourier fornisce

f(τ) =4A

π

∞∑j=1,3,5,...

1

jsin(αj τ) ; (128)

27

Un confronto tra l’onda quadra e la sua rappresentazione di Fourier troncata alle prime trearmoniche non nulle e mostrata in Fig.(8). La risposta dell’oscillatore all’onda quadra sarafornita dalla (124) adattata al caso in esame

xf (τ) =1

k

4A

π

∞∑j=1,3,5,...

Gjj

sin(αj τ − φ3j)

; (129)

Un grafico molto importante si ottiene sovrapponendo lo spettro della forzante (una caratteristicadell’ingresso) al fattore di amplificazione (una caratteristica del sistema): in questo modo epossibile visualizzare a colpo d’occhio le armoniche che saranno amplificate oppure ridotte.

La Fig.(9) si riferisce ad un oscillatore con caratteristiche ζ = 0.2, ω = 10. Lo spettrodell’onda quadra la variare della pulsazione e mostrato con dei pallini blu: il primo pallino risiedenel punto (α, b1) = (π, 4/π), il secondo in (2α, b2) = (2π, 0), il terzo in (3α, b3) = (3π, 4/(3π)) ecosı via; si nota che i pallini in posizione dispari hanno valori sempre piu bassi, mentre i pallini inposizione pari hanno valore nullo. La curva continua rappresenta il grafico di G(ζ, β) al variaredella pulsazione, e presenta il massimo in prossimita della pulsazione naturale ω = 10.

La terza armonica ha pulsazione 3π ' 9.424, un valore molto vicino a quello della pulsazionenaturale e dunque vicino alla risonanza. I quadrati rossi rappresentano lo spettro del moto xf emostrano l’effetto del fattore di amplificazione: il valore della loro ordinata e dato dal prodottobj G(ζ, βj). Si nota che la prima armonica, alta, viene leggermente amplificata; la secondaarmonica ha valore nullo; la terza armonica, meno importante della prima, viene amplificatatanto che il suo contributo diventa paragonabile a quello della prima armonica; da qui in poi, icontributi sono trascurabili.

�

�

�

�

�

�

�

�

�

��

��

��

��

��

��

�

�

�� � � � � � � �

10 20 30 40 50 60 70

rad

sec

0.5

1.0

1.5

2.0

2.5

Adf

Figura 9: Grafico del fattore di amplificazione G(ζ, β) per il caso ζ = 0.2, ω = 10, al variaredella pulsazione (curva blu). I pallini blu rappresentano lo spettro bi dell’onda quadra, mentrei quadrati rossi sono lo spettro della risposta xf ; la posizione relativa del quadrato rispetto alpallino mostra l’effetto del fattore di amplificazione sulle varie armoniche.

28

4.6 Analisi nel dominio della frequenza

Fino ad ora abbiamo risolto le equazioni del moto nel dominio del tempo, ossia, cercando alfunzione τ 7→ x(τ). Inoltre, abbiamo appena visto come sia importante determinare la rispostaad una forzante periodica, e come tale risposta dipenda dal contenuto armonico della forzante.Tutto cio suggerisce di studiare il moto del pendolo nel cosiddetto dominio della frequenza: datauna forzante con un determinato spettro, come sara fatto lo spettro della risposta?

Data la forzante di periodo Ta, con α = 2π/Ta = α1 armonica fondamentale, le importantirelazioni di Eulero forniscono

cos(αj τ) =1

2[exp(iαj τ) + exp(−iαj τ)] , sin(αj τ) = − i

2[exp(iαj τ)− exp(−img αj τ)] .

(130)Tali relazioni permettono di rappresentare la serie di Fourier (116) in forma esponenziale

f(τ) =∞∑

j=−∞Pj exp(iαj τ) . (131)

I coefficienti della serie Pj saranno in questo caso numeri complessi, dati dalla relazione

Pj =1

Ta

∫ Ta

0f(τ) exp(−iαj τ) dτ , j = 0, ±1, ±2, . . . . (132)

Si noti che, per definizione, i coefficienti Pj e P−j sono complessi coniugati; grazie a questo,i termini immaginari della serie (131) si elidono a vicenda e si ottiene una funzione reale. Inumeri complessi Pj definiscono lo spettro della forzante, analogamente ai numeri reali aj e bj .La risposta alla forzante si ottiene moltiplicando lo spettro Pj per il fattore di amplificazionecomplesso Hj definito da

Hj = H(ζ, βj) =1

(1− β2j )2 + i (2 ζ βj)

. (133)

Dunque, le componenti armoniche di pulsazione αj presenti nella forzante saranno amplificatedi Hj volte, producendo un’uscita di intensita Hj Pj .

Algoritmo

1. f(τ) funzione di periodo Ta

2. Sviluppo in serie di Fourier:

f(τ) = ao1

2+∞∑j=1

[ aj cos(αj τ) + bj sin(αj τ) ] , serie reale

f(τ) =

∞∑j=−∞

Pj exp(iαj τ) , serie complessa

(134)

3. Spettroao, aj , bj ∈ R , j = 1, 2, . . . , spettro reale

Pj ∈ C , j = ±1,±2, . . . , spettro complesso(135)

29

4. Amplificazione:Gj aj , Gj bj , amp. reale

Hj Pj , amp. complessa(136)

5. Campionamento della funzione negli istanti tj = j∆τ , j = 0, 1, . . .

fj = f(τj)

30

4.7 La Funzione Impulso

La funzione impulso, indicata con δ, e chiamata anche funzione di Dirac, e definita dalla richiesta

δ(τ) = 0 , τ 6= 0 ,

∫ ∞−∞

δ(τ) dτ = 1 . (137)

Si tratta di una funzione molto particolare, nulla ovunque tranne che in un punto, e che haintegrale pari ad uno. La funzione di Dirac puo essere costruita facendo un limite: consideriamola funzione:

δε(τ) =

1

ε, −ε

2< τ <

ε

2;

0 , altrove.

(138)

La funzione δε(τ) e diversa da zero solo nell’intervallo ε a cavallo dell’origine, dove vale 1/ε; ilsuo integrale vale dunque 1: base x altezza = ε × 1/ε = 1. Al tendere di ε a zero, la funzioneδε(τ) assume valori sempre piu elevati, in un intervallo sempre piu ristretto, ed il suo integralerimane sempre pari ad uno, vedi Fig.(10); possiamo allora scrivere δ(τ) = limε→0 δε(τ).

δε(τ)

τ

ε

1

ε

δε(τ)

τ

ε

1

ε

δε(τ)

τ

ε

1

ε

Figura 10: La funzione δε(τ) assume la forma di un rettangolo sempre piu allungato al tenderea zero di ε. L’area di tale rettangolo rimane costante ed uguale ad uno.

L’impulso δ(τ) puo essere traslato in punti diversi dall’origine considerando la funzione compostaδ(τ − τ) che avra valore diverso da zero solo in τ = τ . Data la proprieta definitoria (137),possiamo usare la funzione δ(τ) per valutare una generica funzione in un istante prescelto:∫ ∞

−∞δ(τ − τ) f(τ) dτ = f(τ) . (139)

Quindi, la funzione δ(τ − τ) f(τ) vale zero ovunque tranne che in τ = τ , ed il suo integrale eproprio il valore di f in τ .

4.8 L’Impulso Meccanico

Nell’ambito della meccanica la funzione δ viene usata per rappresentare una forza impulsiva,ovvero un impulso meccanico. Per quantificare l’effetto di un impulso meccanico, ricordiamo ladefinizione di quantita di moto p(τ):

v(τ) = x(τ) , p(τ) = mv(τ) . (140)

La prima equazione definisce la velocita v(τ) a partire dal moto x(τ): si tratta di una equazionedi congruenza; la seconda equazione lega una nozione cinematica, la velocita, ad una dinamica, la

31

δ(τ)

τ

δ(τ − τ)

ττ

Figura 11: La funzione δ(τ) e zero ovunque tranne nell’origine dove assume valore infinito(sinistra); la funzione δ(τ − τ) e zero ovunque tranne che in τ = τ (destra).

quantita di moto: si tratta di una equazione costitutiva; la costante m, la massa, e un parametromateriale. Scriviamo l’equazione di bilancio delle forze nella sua forma originaria, in termini diquantita di moto:

p(τ) = f(τ) , ∀t ∈ T , bilancio delle forze, verificato ∀t ∈ T ;

p(0) = po bilancio della quantita di moto, verificato per t = 0.(141)

Nella (141) la forza f(τ) rappresenta la risultante di tutte le forze agenti, a meno della forzad’inerzia. Nel caso in cui f(τ) = δ(τ), possiamo integrare l’equazione di bilancio tra τ = −ε eτ = ε, per ottenere:

p(τ) = δ(τ) ,∀t ∈ T , ⇒∫ ε

−εp(τ) dτ = p(ε)− p(−ε) =

∫ ε

−εδ(τ) dτ = 1 . (142)

Osservazione. La funzione δ non e una funzione continua, ma appartiene ad una classe difunzioni molto particolari dette distribuzioni, che non tratteremo. La equazione p = δ cheabbiamo appena scritto non ha senso in τ = 0: chi sara mai quella funzione p la cui derivatafornisce δ? Per rispondere in modo corretto a questa domanda si dovrebbe modificare il concettodi derivata; senza entrare nei dettagli, ci accontentiamo di dare un senso alla p = δ per il tramitedell’integrale che compare nella (142) �

La (142)2 vale anche al limite per ε che tende a zero, e fornisce:

p(0+)− p(0−) = 1 . (143)

Abbiamo dunque scoperto che una forza impulsiva in τ = 0 provoca un salto della quantita dimoto dal valore che aveva subito a sinistra di τ = 0, indicato con p(0−), al nuovo valore assuntosubito a destra di τ = 0, indicato con p(0+); poiche per valori positivi di τ la forza impulsiva enulla, il sistema manterra constante nel tempo la nuova quantita di moto acquisita con l’impulso.Allora, il problema

p(τ) = δ(τ) ,∀t ∈ T , p(0−) = 0 , (144)

ha come soluzione

p(0+) = 1 , ⇒ v(τ) =1

m= cost . (145)

Le precedenti considerazioni mostrano che i due seguenti problemi sono equivalenti, nel sensoche hanno la stessa soluzione:

p(τ) = δ(τ) ,∀t ∈ T , p(0−) = 0 , forzante pari a δ e condizione iniziale omogenea;

p(τ) = 0 , ∀t ∈ T , p(0) = 1 , forzante nulla e condizione iniziale unitaria;(146)

32

L’equivalenza dei problemi (146) ha i suoi vantaggi: se oltre all’impulso agisce anche una forzantegenerica f(τ), possiamo riscrivere la (142) nel seguente modo

p(τ) = δ(τ) + f(τ) , ∀t ∈ T , ⇒∫ ε

−εp(τ) dτ = p(ε)− p(−ε) =

∫ ε

εδ(τ) dτ +

∫ ε

εf(τ) dτ = 1 .

(147)Infatti, essendo la f(τ) una funzione regolare, il suo integrale tra −ε e ε svanisce al tendere azero di ε. Allora, come prima, i due problemi seguenti sono equivalenti:

p(τ) = δ(τ) + f(τ) , ∀t ∈ T , p(0−) = 0 , forzante pari a δ + f e condizione omogenea;

p(τ) = f(τ) ,∀t ∈ T , p(0) = 1 , forzante pari a f e condizione unitaria;(148)

4.9 La Risposta all’Impulso dell’Oscillatore

La risposta all’impulso e una nozione molto importante della meccanica delle vibrazioni. Consi-deriamo un oscillatore soggetto ad una forzante impulsiva; l’equazione di bilancio dell’oscillatoresemplice e la seguente

mx(τ) + c x(τ) + k x(τ) = δ(τ) , ∀τ ∈ T . (149)

Possiamo procedere come in (147), ossia, pensando al termine c x(τ)+k x(τ) come una ulterioreforza che si aggiunge al problema: integriamo tutti i termini tra −ε e ε∫ ε

−εmx(τ) dτ +

∫ ε

−εc x(τ) dτ +

∫ ε

−εk x(τ) dτ =

∫ ε

−εδ(τ) dτ = 1 . (150)

Svolgendo il primo ed il secondo integrale si ottiene poi

m [ x(ε)− x(−ε) ] + c [x(ε)− x(−ε) ] +

∫ ε

−εk x(τ) dτ = 1 . (151)

Nel limite per ε che va zero, poiche x(τ) e una funzione continua, il secondo e terzo addendo deltermine di sinistra scompaiono, e si ritrova il risultato dell’esempio gia discusso precedentemente.Dunque, il problema in cui la forza impulsiva compare come forzante e le condizioni iniziali sonoomogenee:

mx(τ) + c x(τ) + k x(τ) = δ(τ) , x(0) = 0 , x(0) = 0 , (152)

e equivalente al problema in cui la forzante e nulla e la condizione sulla velocita iniziale e nonomogenea:

mx(τ) + c x(τ) + k x(τ) = 0 , x(0) = 0 , x(0) =1

m, (153)

La risposta all’impulso, indicata con g(τ) e chiamata anche funzione di Green a ricordo delmatematico G. Green, e dunque la soluzione dell’equazione omogenea con particolari condizioniiniziali. Nel caso di sistema smorzato, 0 < ζ < 1, abbiamo:

xom(τ) = exp(−ζ ω τ)

(xo cos(ωd τ) +

vo + xoζ ω

ωdsin(ωd τ)

), (154)

dove ωd = ω√

(1 − ζ2); dunque, ponendo xo = 0, vo = 1/m, abbiamo la risposta all’impulso,valida per τ > 0:

g(τ) =1

mωdexp(−ζ ω τ) sin(ωd τ) =

ω

k√

(1− ζ2)exp(−ζ ω τ) sin(ωd τ) . (155)

33

Scrivendo il bilancio delle forze in forma compatta, (28), possiamo dire che la risposta all’impulsoe la soluzione del seguente problema

Lg(τ) = δ(τ) , ∀τ ∈ T , x(0) = 0 , x(0) = 0 . (156)

−1 0 1 2 3 4 5 6 7 8 9 10−2

−1

0

1

2

τ

k g , δ

k gδ

Figura 12: Risposta dell’oscillatore (blu) all’impulso (rosso); ζ = 0.1, ω = 2. La risposta tendeasintoticamente al valore a riposo x = 0.

4.10 La Funzione Gradino

La funzione gradino, indicata con h e chiamata anche funzione di Heaviside a ricordo dell’inge-gnere O. Heaviside, e definita dalla

h(τ) =

0 , τ < 0 ;

1 , τ > 0 .(157)

Anche questa funzione e molto particolare, costante ovunque tranne che in un punto, dovesubisce un salto. La funzione gradino puo essere definita a partire dall’impulso nel seguentemodo:

h(τ) =

∫ τ

−∞δ(s) ds . (158)

Abbiamo gia visto una equazione del tipo (158): si tratta della (142) che e stata usata per dareun senso alla primitiva della funzione δ. Possiamo allora dire che il gradino h e la primitivadell’impulso δ:

h(τ) = δ(τ) . (159)

Il gradino h(τ) puo essere traslato in punti diversi dall’origine considerando la funzione compostah(τ − τ) che avra il salto in τ = τ .Possiamo utilizzare la funzione gradino per introdurre un salto in una generica funzione continua:data f(τ), la funzione f(τ)h(τ − τ) agisce nel seguente modo:

f(τ)h(τ − τ) =

0 , τ < τ ;

f(τ) , τ > τ .(160)

34

h(τ)

τ

h(τ − τ)

ττ

Figura 13: La funzione h(τ) salta in τ = 0 da zero ad uno (sinistra); la funzione h(τ − τ) ha ilsalto in τ = τ (destra).

4.11 La Risposta al Gradino dell’Oscillatore

Possiamo utilizzare la risposta all’impulso g(τ) gia trovata, vedi (155), per ottenere senza troppafatica la risposta dell’oscillatore soggetto ad una forzante a gradino. Ripartiamo dalla (156)1:

Lg(τ) = δ(τ) , ∀τ ∈ T ; (161)

integrando entrambe i termini tra −∞ e τ , e ricordando la (158), abbiamo∫ τ

−∞Lg(s) ds =

∫ τ

−∞δ(s) ds = h(τ) , ∀τ ∈ T . (162)

L’operatore L e l’integrazione commutano; allora∫ τ

−∞Lg(s) ds = L

∫ τ

−∞g(s) ds = h(τ) , ∀τ ∈ T . (163)

Dunque, il problema L con forzante a gradino, ha come soluzione l’integrale della funzione g;indicando con s(τ) tale soluzione e ricordando che g(s) ha senso solo per τ > 0, possiamoscrivere:

s(τ) =

∫ τ

−∞g(s) ds =

∫ τ

0g(s) ds

=1

k

[1− e−ζ ω τ

(cos(ωd τ) +

ζ ω

ωdsin(ωd τ)

)].

(164)

Scrivendo il bilancio delle forze in forma compatta, (28), possiamo dire che la risposta al gradinoe la soluzione del seguente problema

Ls(τ) = h(τ) , ∀τ ∈ T , x(0) = 0 , x(0) = 0 . (165)

Osservazione. Le due soluzioni g(τ) e s(τ) hanno valore solo per τ > 0; possiamo esprimerein modo sintetico questo fatto utilizzando la proprieta (160) per ridefinire le due soluzioni comesegue:

g(τ) =1

k

[ω√

(1− ζ2)exp(−ζ ω τ) sin(ωd τ)

]h(τ) ,

s(τ) =1

k

[1− e−ζ ωd τ

(cos(ωd τ) +

ζ ω

ωdsin(ωd τ)

)]h(τ) .

(166)

35

−1 0 1 2 3 4 5 6 7 8 9 10−2

−1

0

1

2

τ

kg,ks,h

k sh

k g

Figura 14: Risposta dell’oscillatore (blu) al gradino (rosso); ζ = 0.1, ω = 2. La risposta tendeasintoticamente al valore x = 1, corrispondente ad una forzante stazionaria. La linea tratteggiatamostra la risposta all’impulso riportata nella figura precedente; confrontando le due risposte sinota che l’impulso provoca oscillazioni molto piu ampie.

4.11.1 Esempio: gradino rettangolare

La nozione di risposta al gradino permette di ricavare in modo semplice la risposta ad unaforzante ‘rettangolare’ indicata con r(τ), somma di due gradini, uno opposto all’altro e sfalsatinel tempo

r(τ) = ro [h(τ + τ)− h(τ − τ) ] (167)

Poiche il sistema e lineare, la risposta sara data dalla somma delle singole risposte al gradino;utilizzando la (166) si ottiene in modo immediato

x(τ) = ro [ s(τ + τ)− s(τ − τ) ]

=rok

[1− e(−ζ ωd (τ+τ))

(cos(ωd (τ + τ)) +

ζ ω

ωdsin(ωd (τ + τ))

)]h(τ + τ)

− rok

[1− e(−ζ ωd (τ−τ))

(cos(ωd (τ − τ)) +

ζ ω

ωdsin(ωd (τ − τ))

)]h(τ − τ) .

(168)

La Fig.(14) mostra la risposta di un oscillatore non smorzato (nero) al ‘rettangolo’ r(τ) (campi-tura grigia), calcolata con i seguenti valori dei parametri ζ = 0, ω = 3, τ = 2. La funzione r(τ)e la somma del gradino positivo in τ = −τ (rosso) e di quello negativo in τ = τ (blu). Quandola forzante torna a zero, la risposta diventa armonica attorno al valore x = 0.

4.12 L’integrale di convoluzione

Data una forzante generica f(τ), definita per τ > 0, costruiamo la seguente funzione, prodottodi un impulso posto in τ = s e della funzione data valuta in s:

f(s) δ(τ − s) . (169)

Data la proprieta dell’impulso (139), la funzione appena definita verifica la seguente equazione∫ τ

0f(s) δ(τ − s) ds = f(τ) ; (170)

36

−τ 0 τ 2 τ

−2

−1

0

1

2

τ

k x

Figura 15: Risposta dell’oscillatore non smorzato (nero) al ‘rettangolo’ r(τ) (campitura grigia);ζ = 0., ω = 3, τ = 2. La funzione r(τ) e la somma del gradino positivo in τ = −τ (rosso) e diquello negativo in τ = τ (blu). Quando la forzante torna a zero, la risposta diventa armonicaattorno al valore x = 0.

l’integrale che compare nella precedente equazione e detto integrale di convoluzione e ammettela seguente interpretazione: la funzione f(τ) e rappresentata come una somma di infiniti termini(l’integrale) di impulsi che in ogni punto s hanno il valore f(s).

Sapendo che la risposta all’impulso e descritta dalla funzione di Green g e che l’operatoredi bilancio e lineare, utilizziamo di nuovo il bilancio delle forze scritto in forma compatta, vedi(28), per formulare il seguente problema

Lf(s) g(τ − s) = f(s) δ(τ − s) , ∀τ > 0 , x(0) = 0 , x(0) = 0 . (171)

Integrando entrambe i termini tra 0 e τ e ricordando che l’operatore L e l’integrazione commu-tano, abbiamo∫ τ

0Lf(s) g(τ − s) ds = L

∫ τ

0f(s) g(τ − s) ds =

∫ τ

0f(s) δ(τ − s) = f(τ) , ∀τ > 0 . (172)

La relazione appena trovata dice che la soluzione x(τ) del problema con forzante qualsiasi f(τ)e condizioni iniziali omogenee e dato dall’integrale di convoluzione della forzante per lafunzione di Green: riassumendo, abbiamo

IN: f(τ) & x(0) = 0 , x(0) = 0 . ⇒ OUT: x(τ) =

∫ τ

0f(s) g(τ − s) ds . (173)

La traslazione τ − s che compare nell’integrale di convoluzione puo essere fatta su uno dei dueprodotti senza alterare il risultato; possiamo allora scrivere

x(τ) =

∫ τ

0f(s) g(τ − s) ds =

∫ τ

0f(τ − s) g(s) ds , τ > 0 . (174)

Gli integrali di convoluzione non sempre sono semplici da calcolare; la scelta di traslare la forzanteoppure la funzione di Green viene fatta in base considerazioni di convenienza computazionale.

37

Nel caso dell’oscillatore, la risposta all’impulso e rappresentata dalla (166)1; dunque, larisposta alla forzante generica f(τ), con condizioni iniziali omogenee, sara data dalla

x(τ) =

∫ τ

0f(s) g(τ − s) ds =

ω

k√

(1− ζ2)

∫ τ

0f(τ) exp[−ζ ω (τ − s)] sin[ωd (τ − s)] ds ; (175)

si ricordi che la funzione x(τ) e definita solo per τ > 0.

4.12.1 Esempio: convoluzione armonica

Usiamo la tecnica dell’integrale di convoluzione per calcolare la risposta dell’oscillatore nonsmorzato ad una forzante nulla per τ < 0 ed armonica per τ > 0, del tipo

f(τ) = k A sin(α τ)h(τ) . (176)

Inserendo la (176) nella (175) e ponendo ζ = 0, abbiamo

x(τ) = Aω

∫ τ

0sin(α s) sin[ω (τ − s)] ds . (177)

Il prodotto tra funzioni armoniche sotto integrale puo essere trasformato utilizzando la seguenterelazione trigonometrica

sin(u) sin(v) =cos(u− v)− cos(u+ v)

2; (178)

si ottiene dunque, dopo alcune manipolazioni

x(τ) =A

1− β2[ sin(α τ)− β sin(ω τ) ]h(τ) ; (179)

si noti il gradino h(τ) che compare al termine della precedente espressione: in questo modoviene reso esplicito il fatto che tale risposta e nulla per τ < 0. Usando la soluzione con forzantearmonica (87) trovata per altra via, supponendo φ3(0, β) = 0, abbiamo

xg(τ) = xom(τ) + xf (τ) = a cos(ω τ) + b sin(ω τ) +A

1− β2sin(α τ) (180)

Le due costanti a e b si trovano per il tramite delle condizioni iniziali

xg(0) = a , xg(0) = b ω +Aα

1− β2⇒ a = 0 , b =

Aαω

α2 − ω2. (181)

Inserendo i valori delle costanti nella soluzione generale xg si trova lo stesso risultato riportatonella (179) a meno della funzione gradino.

4.13 Forzanti notevoli: la mezza-armonica e l’urto

Puo accadere che le strutture siano soggette a carichi molto elevati, che agiscono per intervallidi tempo molto brevi rispetto al periodo naturale della struttura. Qui analizziamo due forzantidi questo tipo, la mezza-armonica e l’urto (DA COMPLETARE).

38

4.13.1 Mezza armonica

Una forza di breve durata, detta shock in inglese, puo essere caratterizzata dal massimo valoreche raggiunge, dalla durata Ts e dal suo andamento temporale. Una rappresentazione esplicitadi tale evento molto usata e la funzione seno troncata al primo mezzo periodo, ossia, la funzione

f(τ) = k A [ sin(αs τ)h(τ) + sin(αs (τ − Ts))h(τ − Ts) ] , αs =π

Ts; (182)

attenzione: Ts non e il periodo della funzione seno, ma la sua meta, ossia, la durata di mezzaoscillazione. La (179) fornisce la risposta ad una forzante armonica con il gradino; poiche il

0 Ts 2Ts 3Ts 4Ts 5Ts 6Ts

−2

−1

0

1

2

τ

f

k A

f(τ)/(k A)

sin(αs τ)h(τ)

sin(αs (τ − Ts))h(τ − Ts)

Figura 16: La funzione mezza armonica (nera) e ottenuta sommando un seno-gradino (magenta)con un altro seno-gradino traslato di Ts (tratteggiato). αs = 3, Ts = π/3

sistema e lineare, la risposta all’ingresso (182) sara data da

x(τ) =A

1− β2s

([ sin(αs τ)−βs sin(ω τ) ]h(τ)+[ sin(αs (τ−Ts))−βs sin(ω (τ−Ts)) ]h(τ−Ts)

),

(183)con βs = αs/ω. Cerchiamo ora il massimo della risposta, assumendo che esso si verifichi duranteil periodo di tempo in cui agisce la forzante, ossia, per τ ∈ (0, Ts); consideriamo dunque soloil coefficiente di h(τ) che compare nella (183) e cerchiamo gli zeri della sua derivata rispetto altempo

d

d τ[ sin(αs τ)− βs sin(ω τ) ] = αs [ cos(αs τ)− cos(ω τ) ] = 0 . (184)

La relazione trigonometrica

cos(u)− cos(v) = −2 sin

(u+ v

2

)sin

(u− v

2

)(185)

permette di riscrivere la (184) in una forma piu agevole per la ricerca degli zeri

cos(αs τ)− cos(ω τ) = 2 sin

(ω + α

2τ

)sin

(ω − α

2τ

)= 0 . (186)

39

Tale espressione si annulla in un numero infinito di istanti, ma la condizione τ1,2 ∈ (0, Ts) poneun limite superiore agli istanti da considerare

τ1,2 =i 2π

ω ± α, i = 1, 2, . . . & τ1,2 ∈ (0, Ts) ⇒ i =<

1

2

(1± 1

βs

); (187)

in questi istanti la (183) assume i valori

x1,2(τ1,2) =A

1∓ βssin

(i 2π βs1± βs

), i =<

1

2

(1± 1

βs

). (188)

Esaminando la precedente relazione risulta che il massimo si ha negli istanti τ1 e vale

xmax =A

1− βssin

(i 2π βs1 + βs

), i =<

1

2

(1± 1

βs

). (189)

�10 10 20 30 40 50 Τ

�0.5

0.5

1.0

1.5

xA

Β�0.4

Β�0.3

Β�0.2

Β�0.1

Figura 17: Risposta alla mezza armonica per vari valori di βs, con ω = 1.

40