Tensioni e deformazioni interne

Una trave soggetta a carichi ortogonali, si inflette

spazzando il piano di inflessione

La direzione di inflessione, se c’è simmetria rispetto al

piano xy, è diretta secondo y

Si ha flessione pura se la sola sollecitazione

è dovuta al momento flettente, senza taglio

Si ha flessione non uniforme se alla flessione

viene associato un taglio Fless. pura

F. Non unif. F. Non unif.

Come si vedrà, in genere le zone della

sezione più sollecitate a flessione sono

lontane da quelle sollecitate a taglio e quindi si

disaccoppiano gli effetti

CURVATURA DI UNA TRAVE (piccoli spostamenti)

La trave si oppone al momento incurvandosi, e ciò è responsabile dell’insorgere di tensioni

Il centro di curvatura O’ è identificato dalla normale a

due punti m1 e m2 distanti dx

Il raggio di curvatura (ed il suo inverso ) rendono

la trave tanto meno rettilinea quanto maggiore è M

1

d ds 1d

ds

Nell’ambito dei piccoli spostamenti

si può confondere ds con dx

1d

dx

Altro modo di vedere le cose: curvatura positiva se il centro di curvatura

si pone verso la direzione positiva delle y

In questa trattazione si assumerà la curvatura positiva (derivata seconda

positiva) che si instaura per effetto di un momento flettente positivo

Basandosi solo su considerazioni di

simmetria si può dimostrare che:

CONSIDERAZIONI DI CONGRUENZA

L’angolo d è dunque il medesimo per

la fibra e-f e quella neutra s-s 1

xdx dx

dy

x

y

Sezioni piane e perpendicolari alla linea

d’asse rimangono piane anche dopo

deformazione

La perpendicolarità con la linea d’asse si

mantiene anche dopo la deformazione

Alcune linee d’asse si comprimeranno

TOP ed altre si allungheranno BOTTOM

Esiste una linea d’asse particolare

ASSE NEUTRO per la quale le fibre non

si allungano né si accorciano

La sollecitazione che ci si aspetta è quindi assiale, in quanto alcune fibre (estradosso) si

allungheranno, le altre (intradosso) si accorceranno.

Dato che la sollecitazione è monodimensionale (σx) si

osserverà anche una deformazione nelle altre due direzioni

y x

z x

y

y

Centro curvatura principale

Quindi le travi prismatiche si incurvano in tutti e

tre i piani, ma si tensionano solo sul piano x-y

Curvatura secondaria

y z

Centro curvatura secondario z

Per il calcolo delle tensioni che si creano per effetto del momento applicato, si hanno a

disposizione le due equazioni di equilibrio, longitudinale e dei momenti

0 ;x xA A

dA y dA M

Se l’asse di sollecitazione è di simmetria (y) l’asse baricentrico appartiene al piano neutro

Per la simmetria su y il piano neutro è

piano principale d’inerzia

Il momento statico della sezione rispetto al piano

neutro è nullo – l’asse neutro (traccia piano

neutro su piano di simmetria) è baricentrico

TENSIONE NORMALE

= ; 0 ; 0x x y z

yE E

L’equazione di Hooke, applicata al caso monodimensionale, fornisce l’andamento della tensione

Quindi anche la tensione, come la curvatura,

segue un andamento lineare con la distanza

dall’asse neutro

Dalla I: 0A

n

Ey dA

0A

y dA

Dalla convenzione dei segni adottata, un

momento positivo sposta il centro di

curvatura nel semispazio delle y positive

Dalla II: 2

x zA A

E EM y dA y dA J

1

z

M

E J

Jz è il momento di inerzia che viene detto z in quanto misura la distanza y dall’asse neutro z

Il termine EJz per analogia con la sollecitazione di trazione, viene anche indicato come

rigidezza flessionale

Combinando le due equazioni si ottiene lo stato di sollecitazione che risulta variabile

linearmente (farfalla)

z

M yy

J

Per una sezione simmetrica e

bilanciata rispetto baricentro

La tensione risulta massima dove massima è la distanza dall’asse neutro di flessione

SEZIONE CIRCOLARE PIENA E CAVA

Piena:

4

64zJ D

Cava:

4 4

64zJ D d

Il massimo valore si ha in corrispondenza del raggio massimo

, 3

32

2 x D

z

M D M

J D

, 4 4

32

2 x D

z

M D M D

J D d

Il massimo valore si ha in corrispondenza della massima distanza dall’asse neutro

, 2

6

2 x D

z

M h M

J b h

, 33

6

2 2 2x D

z

M D M h

J bh b s h s

SEZIONE RETTANGOLARE PIENA E CAVA

Piena:

31

12zJ bh

Cava:

331

2 212

zJ bh b s h s

O

Ripasso: Leggi per il trasporto dei momenti d’inerzia

di sezione

O

O

X x X

Y y Y

Su un nuovo SdR (XY) spostato

in O di coordinate XO YO:

2 2 2 2X O O O

A A A A

J y Y dA y dA Y dA Y ydA

22X x O x OJ J Y S Y A 22Y y O y OJ J X S X A

XY O O xy O y O x O O

A

J x X y Y dA J X S Y S X Y A Momento

centrifugo:

Se il riferimento xy ha per origine il baricentro (O G), le trasformazioni sono:

2

2

g

g

g

X x G

Y y G

XY xy G G

J J Y A

J J X A

J J X Y A

L’utilità di queste trasformazioni è notevole, in

quanto il calcolo dei momenti di inerzia si semplifica

molto suddividendo la sezione in parti elementari,

ciascuna delle quali viene sommata dopo averla

riportata al baricentro dell’intera struttura

Trasformazioni di Huygens

O

Esempio

Sezione resistente

La struttura in acciaio è montata a sbalzo e presenta un carico distribuito

Calcolare i valori massimo e minimo della tensione assiale

Soluzione:

Dato che la sezione è costante, i valori

massimi e minimi di tensione si avranno là

dove risulta massimo il momento flettente

3375 N 10125 N

0 N

Diagramma del taglio

Diagramma del momento 0

0

x

M M V x dx

Bisogna innanzitutto calcolare il baricentro

della sezione (mediante la media pesata)

1 2 3

1 2 3

40 74 40 G

A A Ay

A A A

z

yg

y

80

276 12 12

68

61.52 Gy mm

I momenti di inerzia baricentrici delle 3

aree sono:

3 4

1

112 80 512000

12I mm

3 4

2

1276 12 39744

12I mm

4

3 512000 I mm

Utilizzando il teorema di Huygens si

calcola il momento di inerzia totale

2 2 6 42 512000+ 80 12 61.52 - 40 39744 + 276 12 74 - 61.52 = 2.469 10 totI mm

Tensione al TOP 2

6

3375 = 80 - 61.52 = 25.3 N

2.469 10Top mm

z

M yy

J

2

6

3375 = -61.52 = 84.2 N

2.469 10Bot mm

Tensione al BOT

A1 A3

A2

Massima trazione al Bottom 47.3 MPa

Tensione al TOP 2

6

1898 = 80 -61.52 = 14.2 N

2.469 10Top mm

z

M yy

J

2

6

1898 = -61.52 = 47.3 N

2.469 10Bot mm

Tensione al BOT

Massima compressione al Bottom - 84.2 MPa

MODULO DELLA SEZIONE

Ciascuna sezione può anche essere caratterizzata da un modulo, che consente il passaggio

immediato dal momento applicato alla tensione normale (Top o Bottom)

top

Top

z

M y

J Top

z Top

M

S

Bot

Bot

z

M y

J Bot

z Bot

M

S

zz

JS

y

4

64z

dJ

3

32z

dS

3

12z

bhJ

2

6z

bhS

Top Bot

PROGETTO DI UNA TRAVE

In genere è noto il momento massimo applicato e si sceglie la beam che soddisfa la max

amm

MS

Se la beam non è simmetrica rispetto piano neutro oppure se il materiale non ha

comportamento simmetrico trazione-compressione, occorrerà estendere la verifica a entrambe

le posizioni Top e Bottom

In genere sono disponibili travi di molteplici forme e materiali:

In acciaio: per lo più laminate, di carpenteria o saldate se di grandi dimensioni

In alluminio: per lo più estruse

In legno: per lo più incollate e/o chiodate

In cemento armato: per lo più colate in forma

In compositi a fibra: estruse, injection molding, pressofusione, …

EFFICIENZA RELATIVA TRA TRAVI

2

0.1676 6

z

bh AhS Ah A parità di area conta solo l’altezza

3

0.125 32

cerchio

dS A d

3 2

0.1477 6 12 4

quadrato

h dS d A d

Nella sezione quadrata si ha meno inutile materiale sull’asse neutro

La soluzione migliore prevederebbe l’uso di materiale nelle

sole flangie, per cui:

2

22 4

ideale

A hI

0.5 idealeS A h

0.35 effettivoS A h

Questo valore in realtà non può essere raggiunto perché

è necessaria un’anima che tiene lontane le due flange e

che non può essere troppo sottile per non andare

incontro ad instabilità

Prendendo un cerchio di

pari area ad un quadrato

2d h

2h d

Esempio

Una barriera temporanea all’acqua è realizzata da tavole

orizzontali sostenute da pali verticali infissi nel terreno.

Calcolare la dimensione dei pali a livello massimo dell’acqua se

la tensione ammissibile del legno è pari a 8.0 MPa.

Soluzione:

Ciascun palo supporta un carico per unità

di lunghezza crescente (triangolare) che

agisce per una larghezza s

0q hs

Il massimo momento si ha alla base e vale

3

0max

2 3 6

q h h h sM

Il modulo della sezione necessario risulta

3

max

6 amm amm

M h sS

3

6

bS 3

amm

sb h

assumendo

310000 /N m 0.8 s m

2.0 h m3

6

10000 0.82.0 0.200

8 10b m

TRAVI A SEZIONE VARIABILE

In molte applicazioni, risparmio di

materiale ed ottimizzazione inducono a

realizzare forme a sezione variabile lungo

l’asse, come negli esempi a lato

Ovviamente, la zona più sollecitata può

non corrispondere al punto ove è

massimo il momento

In genere si usa la variazione di sezione

proprio per minimizzare il peso in favore

di una sollecitazione uniforme

TRAVI A FLESSIONE DI UNIFORME RESISTENZA

Vediamo le possibili configurazioni per

una trave incastrata-libera (clamped)

P

M P x

x

In questo caso è necessario che Jz o Sz varino linearmente

con x

LARGHEZZA VARIABILE

0

cost

2z

P x h

J x

0

cost

z

P x

S x 2

6

lastz

b xS x h

L

P

ALTEZZA VARIABILE

Ora la variabilità lineare di Sx sarà affidata alla variazione della sola altezza

0

cost

z

P x

S x

0

2 6

x

b Ph x

6

amm

Pxh x

b

Ne risulta un profilo parabolico

Ovviamente si potrebbero ancora

impostare modifiche contemporanee di

spessore ed altezza …

Tensioni dovute al taglio

In linea teorica si può avere sollecitazione di solo taglio, ma in

realtà essa si accompagna sempre a momento flettente

x

y

V

V

Ciononostante, anche in presenza di taglio il momento flettente si calcola allo stesso modo

in quanto esso fornisce tensioni normali, mentre il taglio dà tensioni tangenziali, nel

riferimento adottato

Il calcolo della tensione di taglio su una sezione è in realtà assai più

complesso, esso varia sia secondo x che y (in forma parabolica per

una sezione rettangolare)

Proprio per effetto delle forze di

taglio la flessione di due travi

sovrapposte e di un’unica trave di

spessore doppio differiscono

sensibilmente

Spesso, in I approssimazione, si considera il taglio

uniformemente distribuito sulla sezione resistente V

A

In modo più esatto, ma sempre approssimato (Jourawsky) , il taglio viene mediato lungo la

direzione dello spessore (z), e considerato variabile lungo y

sup yxF b y dx

Si consideri l’equilibrio del parallelepipedo ii - rr - ss - jj in direzione x

Sulla faccia superiore agisce una risultante:

Sulla faccia inferiore agisce una risultante nulla (Non sono applicate forze)

Sulle facce laterali – lungo x – agiscono le tensioni dovute ai momenti flettenti M e M+dM

1

z

My y

J

2

z

M dMy y

J

x

xy

Si considera di isolare un elementino assiale (lunghezza dx)

V V

M M+dM

i

i

j

j

r

r

s

s

yx

xy

b dx

y

xy

z

Ricordando che

1 2 z z z z

M M dM dM Vdxy y y y y y

J J J J

1 2( ) ( )

dx 0yxA rr ii A ss jj

y dA y dA b y

Sommando i tre contributi, con il segno dato dall’asse x:

12

yx

x

uguali

Portando fuori dall’integrale le grandezze che rimangono costanti

( ) ( )

yx yx

A i j A i jz z z

V S yVdx Vy dA b y dx y dA

J J b y J b y

Quindi lungo y (essendo costante in z) il taglio varia secondo il momento statico S(y) e lo

spessore della sezione b(y)

Asse baricentrico

yI momenti statici delle due sezioni,

superiore ed inferiore sono uguali!

b y

sup infS S

1

3H

2

3H

2

211 1 1

2

2 2 2 4

h yh b hS y b y y

2

2

2 4yx

V hy y

J

SEZIONE RETTANGOLARE

Il momento statico si può calcolare come area della parte sottesa alla corda ii per la distanza

del suo baricentro dall’asse neutro

Il valore massimo (y=0)

2 3

8 2yx

Vh Vy

J A

Pertanto, il taglio presenta, lungo y, un andamento dominato dal

momento statico – esso si annulla al top/bottom e risulta massimo nella

sezione baricentrica

taglio

y

x

Rispetto al taglio mediato su tutta la sezione, il taglio al baricentro è

superiore del 50 % nella sezione rettangolare

Con alcune cautele la formula di

Jourawsky è applicabile anche a

sezioni non regolari

Tensioni ribaltate

Il tensore delle tensioni dovrà comunque

risultare sempre tangente al profilo esterno,

pertanto, occorre sovrapporre alle tensioni di

taglio di Jourasky un’altra componente xz

(antisimmetrica) che riorienti localmente le .

0

0

sin

R

xA

S y dA r r d dr

3

2 3

00

2cos

3 12

R

x

DS r dr R

3

2

2 3 4

1 2 3

xG

S Ry R

A R Da cui si può ricavare anche l’ordinata del baricentro:

( , ) dA r r d dr Calcolo del momento statico

G

3

max 4

0 64 1 4

0 12 3

V S D VV

J b D D A

SEZIONE CIRCOLARE

La tensione media può calcolarsi anche per una sezione

circolare, tenendo conto le limitazioni sul riorientamento delle

nei bordi non paralleli a y. In particolare sul diametro:

Dato che esiste il semplice legame

= / G tra taglio e scorrimento,

questo ultimo sarà massimo al

centro e nullo al top / bottom

Le sezioni, inizialmente ortogonali all’asse,

si ingobbano

Tuttavia, lo scorrimento è uguale per ogni

fibra assiale, per cui non si instaurano (per

sezioni costanti) sollecitazioni o deformazioni

assiali (taglio puro senza flessione)

Lo spostamento tra due sezioni può essere valutato

mediante la deformazione (scorrimento) media

mediad dx media

T

GA

Fattore di taglio

Lo sforzo di taglio induce l’elemento a

variare di forma (ma non di volume)

secondo un angolo di scorrimento

DEFORMAZIONE A TAGLIO

Il lavoro di deformazione, in accordo al teorema di Clapeyron, è pari all’integrale, lungo la

linea, della metà della tensione di taglio per lo scorrimento medio

1

2meddW V dx

od anche

sul volume

V S y

J b y

2 2

2 2

S y 1

J 2 A

VdW dA dx

b y G

22

2 2

S y 1

2 G JA

VdW dAdx

b y

21

2

VdW dx

GA

dA b J

SA

A 2

i

2

2

i

Il fattore di taglio può essere calcolato

analiticamente per ogni sezione

In sollecitazioni di momento non uniforme

(presenza di taglio) l’andamento delle

nelle flangie presenta due componenti

(ma quella orizzontale è più importante)

TENSIONI DI TAGLIO IN TRAVI FLANGIATE

Area sezione flangia:

11

2 2

hhA b

Area sezione parziale anima:

12 1

2

hA t y

Momento statico:

1 1 1 11 1 2 1

2

2 4 2

h h h h yS y A A y

2 2 2 2

1 1 1 148 8

b tS y h h h y Sostituendo e semplificando

Le tensioni sull’anima si possono calcolare utilizzando la

formula di Jourawsky:

V S y

J b y

1 2 2 2 2

1 1 1

1

4

8

V S y Vb h h t h y

J b y J t

L’unica variabile è y1 , in modo quadratico

1

2 2 2

max 1 10

8 y

Vbh bh th

J t

1 1

2 2

min 12

8 y h

Vbh bh

J t

Generalmente, per le travi flangiate, è l’anima a supportare quasi tutto lo sforzo del taglio

verticale applicato (90-98 %)

In genere si trascura il contributo delle flangie, e si considera il taglio mediato su tutta

l’anima con la semplicissima formula

1

anima

V

t h

Il semplice metodo utilizzato non può essere esteso al calcolo del taglio verticale sulle

flangie, e si trascura la presenza del raccordo circolare, che pure è determinante per

abbassare i picchi di tensione

TRAVI COMPOSTE

In molte applicazioni si ricorre a travi ottenute dall’assemblaggio di più elementi, anche in

materiali differenti, per ottenere ottime performance leggerezza / costo / dimensioni

Il calcolo di queste travi necessita di due passaggi:

Verifica del comportamento della trave a flessione-taglio composta come se

fatta di un sol pezzo

Verifica delle connessioni presenti (chiodature, incollaggi, bullonature, spine,

saldature, …) attraverso il concetto del flusso di taglio

( ) ( )

yxA i j A i j

Vdx dMb y dx y dA y dA

J J

Riprendiamo l’equilibrio introdotto per il taglio, evidenziando la variazione del momento:

Il flusso del taglio f è definito:

1

yx

dM Vf b y y dA y dA

dx J J

Tale flusso (per unità di lunghezza) è utilizzato per verificare le

saldature longitudinali

Nel caso a fianco, il flusso viene calcolato per il tramite del

momento statico esteso a tutta la flangia superiore

(comprensiva delle alette verticali)

Il flusso così calcolato si scaricherà in modo discreto sui rivetti

di connessione

In questo caso il flusso va calcolato in corrispondenza di cc – dd.

L’area evidenziata serve per il calcolo del momento statico.

Il flusso così calcolato si scaricherà in modo discreto sui chiodi

di connessione

V V

f y dA S yJ J

In questo caso il flusso va calcolato alla fine dell’anima, in

corrispondenza delle saldature, ottenendo S(y) dall’area evidenziata

TRAVI SOGGETTE ANCHE A SFORZO NORMALE

In molti casi le travi sono contemporaneamente sollecitate a trazione/compressione e a

forze laterali (flessione semplice o composta)

Se la trave non è troppo sottile il calcolo si può fare sovrapponendo gli effetti

x

N x

A

xy

z

V x S yy

J b y

x

z

M xy y

J

Queste due tensioni sommano i rispettivi contributi

Sovrapposizione delle tensioni

assiale e flessionale

Crescendo ancora il momento M

l’asse neutro può comparire e traslare x

z

N My y

A J

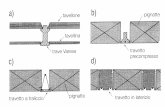
Questa combinazione viene ad esempio utilizzata nel cemento armato precompresso

P Q S

M x Q L x

V x Q

N x S

TRAVI SOGGETTE A CARICO ECCENTRICO

Si tratta di travi nelle quali il carico assiale non è applicato al baricentro Momento di trasporto

x

z

P Pey y

A J

La sovrapposizione comporta in pratica lo

spostamento dell’asse neutro che si ritrova

ponendo nulla la tensione assiale 0

zJy

Ae

È di un certo interesse definire la zona entro la quale l’eccentricità del carico non induca un

cambio nel segno della tensione: materiali non resistenti a trazione/compressione

Considerando anche

l’eccentricità nell’altra direzione

si delimita una zona (rombo)

detto nocciolo della sezione

Sez. rettang.: la condizione limite si ha quando y0 = -h/2

3 1 2

12 6

bh he

bh h

Nel caso ancor più generale di spostamento del carico

secondo due direzioni, l’asse neutro non è più normale

all’asse di sollecitazione né è parallelo agli assi

principali di inerzia

yzx N M

y z

Pe yP Pe z

A J J

L’asse n-n si ricava dall’equazione della retta

che si ottiene annullando la σ:

z z z

y y y

J e Jy z

J e A e

Nei calcoli di si è implicitamente assunto che le deformate fossero tali da non modificare

l’azione dei carichi stessi

Si è anche assunto che le tensioni fossero sempre sovrapponibili e quindi disaccoppiate

fra loro, ciò non è vero se la trave diviene sottile e lo sforzo normale fuori asse fornisce

un momento flettente aggiuntivo

Finora si è sempre trattato di travi ad asse baricentrico rettilineo, in caso contrario

un’altra trattazione è necessaria

CONCENTRAZIONI DI TENSIONE

Valgono le medesime considerazioni fatte per il caso

assiale circa la validità delle soluzioni di St. Venant

Si fa sempre riferimento alle tensioni nette per il calcolo

delle tensioni nominali

3 3

6nom B

My Md

J b h d

La tensione massima si ricava dal fattore K “puramente

geometrico” tabellato e ricavabile in letteratura

Max nom BK

Caso di due intagli simmetrici su

lastra inflessa