Progetto di un solaio - unirc.it...Il solaio è completato da una soletta in calcestruzzo armato...
Transcript of Progetto di un solaio - unirc.it...Il solaio è completato da una soletta in calcestruzzo armato...
-
���
Progetto di un solaio in calcestruzzo armato
-
- Premessa- Descrizione della struttura - Predimensionamento della struttura - Proprietà dei materiali- Analisi dei carichi- Combinazione dei carichi- Disposizione dei carichi- Risoluzione dello schema strutturale- Tracciamento dei diagrammi del momento e del taglio di calcolo e del loro inviluppo- Progetto delle armature longitudinali- Calcolo dei momenti resistenti- Verifiche allo stato limite ultimo per le sollecitazioni di taglio
Indice
-
Si definiscono solai quelle strutture bidimensionali piane caricate ortogonalmente al proprio piano, con prevalente comportamento resistente monodirezionale.I solai fanno parte delle cosiddette chiusure o diaframmi orizzontali, che svolgono il compito di ripartire i carichi sulle travi della struttura in elevazione dell’edificio.La struttura portante del solaio può essere realizzata in calcestruzzo armato, in acciaio o in legno, con la presenza o meno di altri materiali con funzione di alleggerimento, per esempio elementi in laterizio o pani di polistirolo.
Premessa
Impossibile trovare nel file la parte immagine con ID relazione rId7.
-
Descrizione della struttura 1/2
La presente esercitazione riguarda il progetto esecutivo di un solaio tradizionale misto in latero-cemento. Il solaio è costituito da travetti in calcestruzzo armato tra cui si dispongono elementi di alleggerimento in laterizio, denominati pignatte. Il solaio è completato da una soletta in calcestruzzo armato posta al di sopra dei travetti e delle pignatte che, oltre a svolgere le funzioni di ripartizione dei carichi verticali, irrigidisce il solaio nel suo piano al fine di distribuire le azioni sismiche orizzontali tra le strutture verticali. All’intradosso e all’estradosso sono disposti gli strati di finitura (intonaco e pavimento).
-
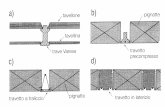
Descrizione della struttura 2/2La disposizione planimetrica del solaio e la direzione dell’orditura dei travetti sono indicate nella seguente pianta di carpenteria.
-
Predimensionamento della struttura 1/2
La precedente normativa (DM 09/01/1996) prescriveva per i solai misti in latero-cemento le limitazioni dimensionali riportate nella seguente tabella.Anche se le NTC08 ne ripropongono solo alcune, è buona norma continuarle a seguire in ogni caso.
Spessore solaio L è la luce della campata più lunga. Poiché una pignatta non è alta meno di 12 cm, l’altezza minima del solaio è 16 cm.
Spessore soletta In genere non si usano solette con spessore maggiore di 5 cm.
Larghezza travettoDimensioni usuali sono . La larghezza del travetto dipende anche dal valore previsto della sollecitazione di taglio.
Larghezza pignattaIn genere l’altezza di una pignatta è sempre un numero pari:
Interasse travetto Un interasse usuale è i = 50 cm, considerando una pignatta larga 40 cm e un travetto largo 10 cm.
H ≥ L 25
s ≥ 4 cm
i ≤15⋅s
b0 ≥ i 8
b0 ≥ 8 cm
bp ≤ 52 cm
H ≥12 cm
b0 = 10 ÷12 cm
12 ÷14 ÷16 ... cm.
-
Predimensionamento della struttura 2/2
Nel nostro caso, poiché L = 550 cm, risulta H = 22 cm. Si pongono, inoltre, s = 4,0 cm, b0 = 10 cm, bp = 40 cm. L’interasse dei travetti è quindi pari a i = 50 cm. Si assume, inoltre, che all’intradosso sia presente un intonaco di spessore 1,5 cm e che all’estradosso vi sia un pavimento in piastrelle di ceramica, posato su un massetto di spessore 3,0 cm
-
La classe del calcestruzzo si sceglie in base alla classe di esposizione della struttura, con riferimento alle norme UNI 11104:2004 e UNI EN 206-1:2006, al fine di garantire un’adeguata durabilità del materiale.La durabilità del calcestruzzo è la capacità di durare nel tempo, resistendo alle azioni aggressive dell’ambiente, agli attacchi chimici, all’abrasione e a ogni altro processo di degrado che coinvolga il conglomerato cementizio e/o le armature metalliche.
Caratteristiche dei materiali
Per la classe di esposizione XC1 si ha:- Calcestruzzo classe C25/30- Acciaio tipo B450C
-
Analisi dei carichi 1/12
L’analisi dei carichi riguarda:
Carichi variabiliDipendono dalla destinazione d’uso dell’edificio e del solaio (copertura, locali interni, balconi)
Determinati i carichi e stabilite le combinazioni di carico più gravose, le sollecitazioni nei travetti del solaio si calcolano con riferimento al seguente schema di trave continua su tre appoggi:
Carichi permanenti strutturali– soletta– travetti– pignatte
Carichi permanenti non strutturali– intonaco– massetto– pavimento– incidenza tramezzi o impermeabilizzazione
-
Analisi dei carichi 2/12
Per comodità di calcolo, l’analisi dei carichi verrà svolta con riferimento a una fascia di solaio larga 1,00 m.
-
3.1.2 Pesi propri dei materiali strutturaliPer la determinazione dei pesi propri strutturali dei più comuni materiali possono essere assunti i valori dei pesi dell’unità di volume riportati nella Tab. 3.1.I
Analisi dei carichi 3/12
Prima di svolgere l’analisi dei carichi, si riportano le indicazioni dei paragrafi 3.1.2, 3.1.3 e 3.1.3.1 delle NTC08.
-
3.1.3 Carichi permanenti non strutturaliSono considerati carichi permanenti non strutturali i carichi non rimovibili durante il normale esercizio della costruzione, quali quelli relativi a tamponature esterne, divisori interni, massetti, isolamenti, pavimenti e rivestimenti del piano di calpestio, intonaci, controsoffitti, impianti ed altro, ancorché in qualche caso sia necessario considerare situazioni transitorie in cui essi non siano presenti. Essi devono essere valutati sulla base delle dimensioni effettive delle opere e dei pesi dell’unità di volume dei materiali costituenti.In linea di massima, in presenza di orizzontamenti anche con orditura unidirezionale ma con capacità di ripartizione trasversale, i carichi permanenti portati e i carichi variabili potranno assumersi, per la verifica d’insieme, come uniformemente ripartiti. In caso contrario, occorre valutarne le effettive distribuzioni.I tramezzi e gli impianti leggeri di edifici per abitazioni e uffici possono assumersi, in genere, come carichi equivalenti distribuiti, purché i solai abbiano adeguata capacità di ripartizione trasversale.
Analisi dei carichi 4/12
-
3.1.3.1 Elementi divisori interniPer gli orizzontamenti degli edifici per abitazioni e uffici, il peso proprio di elementi divisori interni potrà essere ragguagliato ad un carico permanente portato uniformemente distribuito g2k, purché vengano adottate le misure costruttive atte ad assicurare una adeguata ripartizione del carico. Il carico uniformemente distribuito g2k ora definito dipende dal peso proprio per unità di lunghezza G2k delle partizioni nel modo seguente:- per elementi divisori con G2< 1,00 kN/m: g2 = 0,40 kN/m2 - per elementi divisori con 1,00 < G2 < 2,00 kN/m: g2 = 0,80 kN/m2- per elementi divisori con 2,00 < G2 < 3,00 kN/m: g2 = 1,20 kN/m2- per elementi divisori con 3,00 < G2 < 4,00 kN/m: g2 = 1,60 kN/m2- per elementi divisori con 4,00 < G2< 5,00 kN/m: g2 = 2,00 kN/m2 Elementi divisori interni con peso proprio maggiore devono essere considerati in fase di progettazione, tenendo conto del loro effettivo posizionamento sul solaio.
Analisi dei carichi 5/12
-
Pesi specifici di altri materiali ed elementi costruttiviLa Circolare del Ministero dei Lavori Pubblici del 4 luglio 1996 n. 156, tra l’altro, specifica i seguenti ulteriori pesi specifici:
Malta bastarda (intonaci) 19.00 kN/m3
Laterizi forati 8.00 “Muratura di mattoni forati 11.00 “Manto impermeabilizzante (guaina) 0.10 kN/m2
Pavimento di ceramica 0.40 “
Analisi dei carichi 6/12
-
Peso per unità di superficieMateriale Spessore
[m]γ
[kN/m3]Totale
[kN/m2]
intonaco 0.01 19.00 0.19laterizio 0.08 11.00 0.88intonaco 0.01 19.00 0.19Totale al m2 1.26
G2 = 1.26 ⋅3.00 = 3.78 kN/m
Peso proprio unitario delle partizioni interneConsiderando partizioni interne realizzate con mattoni forati di spessore 8 cm, con un intonaco su entrambe le facce di spessore 1.0 cm, si ha
Considerando un’altezza di 3.00 m, il carico unitario vale:
Pertanto, il carico distribuito equivalente risulta pari a
g2 = 1.60 kN/m2
Analisi dei carichi 7/12
-
Solaio per uso residenziale (campate)
Carichi permanenti strutturali G1b [m] h [m] γ [kN/m3] γ [kN/m2] q [kN/m]
Soletta 1.00 0.04 25 1.00
Travetti 2 x 0.10 0.18 25 0.90
Pignatte 2 x 0.40 0.18 8 1.15
G1 = 3.05
Dimensioni:H = 22 cm b0 = 10 cms = 4 cm bp = 40 cmi = 50 cm
22
3
18
1.5 cm
Analisi dei carichi 8/12
-
Carichi permanenti non strutturali G2b [m] h [m] γ [kN/m3] γ [kN/m2] q [kN/m]
Intonaco 1.00 0.015 19 0.29
Massetto 1.00 0.03 21 0.63
Pavimento 1.00 0.40 0.40
Tramezzi 1.00 1.60 1.60
G2 = 2.92
Carico variabile Q Q = 2.00
Solaio per uso residenziale (campate)
Dimensioni:H = 22 cm b0 = 10 cms = 4 cm bp = 40 cmi = 50 cm
22
3
18
1.5 cm
Analisi dei carichi 9/12
-
Carichi permanenti strutturali G1b [m] h [m] γ [kN/m3] γ [kN/m2] q [kN/m]
Soletta 1.00 0.04 25 1.00
Travetti 2 x 0.10 0.14 25 0.70
Pignatte 2 x 0.40 0.14 8 0.90
G1 = 2.60
Solaio a sbalzo (balcone)Lo spessore della parte a sbalzo viene ridotto di 4.0 cm rispetto a quello delle campate per favorire lo smaltimento delle acque meteoriche.
Dimensioni:H = 18 cm b0 = 10 cms = 4 cm bp = 40 cmi = 50 cm
14 18
5
1.5 cm
Analisi dei carichi 10/12
-
Carichi permanenti non strutturali G2b [m] h [m] γ [kN/m3] γ [kN/m2] q [kN/m]
Intonaco 1.00 0.015 19 0.29
Massetto (pendenze) 1.00 0.05 21 1.05
Pavimento 1.00 0.40 0.40
Impermeabilizzazione 1.00 0.10 0.10
G2 = 1.84
Carico variabile Q Q = 4.00
Soletta a sbalzo (balcone)
Dimensioni:H = 18 cm b0 = 10 cms = 4 cm bp = 40 cmi = 50 cm
14 18
5
1.5 cm
Analisi dei carichi 11/12
-
G1 [kN/m] G2 [kN/m] Q [kN/m]
Campata 3.05 2.92 2.00
Sbalzo 2.60 1.84 4.00
Analisi dei carichi 12/12
Tabella riassuntiva
All’estremità dello sbalzo si considera anche un carico concentrato FP= 0,10 kN, corrispondente al peso del parapetto.
-
Fd = γ G1 ⋅G1 + γ G2 ⋅G2 + γ Q ⋅Q
Per la verifica e il progetto allo Stato Limite Ultimo si considera la combinazione fondamentale dei carichi
dove γG1, γG2 e γQsono i coefficienti parziali di sicurezza dei carichi, specificati nella Tabella 2.6.I delle NTC08 per le verifiche di tipo STR.
Combinazione dei carichi
-
Disposizione dei carichi 1/7
Per la determinazione del momento flettente e del taglio, il solaio viene schematizzato come una trave continua su più appoggi.
I valori massimi delle sollecitazioni si ottengono in corrispondenza delle disposizioni più sfavorevoli dei carichi, che possono essere individuate attraverso il seguente ragionamento. Si consideri una trave continua con un numero indefinito di campate, e si applichi su una di esse un carico distribuito uniforme q.
Sezione resistente
-
Disposizione dei carichi 2/7
Il relativo diagramma del momento è riportato nella seguente figura.
Si osserva che:- il carico applicato sulla generica campata induce momenti positivi in quella stessa campata e
in altre in maniera alternata; - lo stesso carico induce momenti negativi sugli appoggi adiacenti e su altri in maniera
alternata. Da queste osservazioni si deducono le seguenti due regole generali:- per ogni campata, il momento massimo positivo si ottiene applicando il carico massimo su
quella campata e sulle altre in maniera alternata (carico a scacchiera), e il carico minimo sulle rimanenti.
- Per ogni appoggio intermedio, il momento massimo negativo si ottiene applicando il carico massimo sulle campate adiacenti e sulle altre in maniera alternata (carico a scacchiera), e il carico minimo sulle rimanenti.
-
Disposizione dei carichi 3/7
Esempi
Tipica disposizione dei carichi per la valutazione dei massimi momenti positivi in campata
Tipica disposizione dei carichi per la valutazione dei massimi momenti negativi sugli appoggi
-
qAB = 1,0 ⋅G1 + 0 ⋅G2 + 0 ⋅Q = 2,60 kN/mqBC = 1,3⋅G1 +1,5 ⋅G2 +1,5 ⋅Q = 1,3⋅3,05+1,5 ⋅2,92+1,5 ⋅2,0 = 11,35 kN/mqCD = 1,0 ⋅G1 + 0 ⋅G2 + 0 ⋅Q = 3,05 kN/m
Disposizione dei carichi 4/7
Per il solaio considerato, si devono considerare le seguenti tre condizioni di carico.
Condizione di carico 1: massimo momento positivo in campata BC.
-
Condizione di carico 2: massimo momento positivo in campata CD e massimo momento negativo sull’appoggio B.
qAB = 1,3⋅G1 +1,5 ⋅G2 +1,5 ⋅Q = 1,3⋅2,60+1,5 ⋅1,84+1,5 ⋅4,0 = 12,14 kN/mqBC = 1,0 ⋅G1 + 0 ⋅G2 + 0 ⋅Q = 3,05 kN/mqCD = 1,3⋅G1 +1,5 ⋅G2 +1,5 ⋅Q = 11,35 kN/m
Disposizione dei carichi 5/7
-
Condizione di carico 3: massimo momento negativo sull’appoggio C.
qAB = 1,0 ⋅G1 + 0 ⋅G2 + 0 ⋅QqBC = 1,3⋅G1 +1,5 ⋅G2 +1,5 ⋅QqCD = 1,3⋅G1 +1,5 ⋅G2 +1,5 ⋅Q
Disposizione dei carichi 6/7
-
Condizione di carico Carico [kN/m]
AB BC CD
1 2.60 11.35 3.05
2 12.14 3.05 11.35
3 2.60 11.35 11.35
Disposizione dei carichi 7/7
Tabella riassuntiva
-
Risoluzione dello schema strutturale 1/8Il metodo delle forze è uno dei possibili metodi per la risoluzione di strutture iperstatiche ed è particolarmente indicato nel caso di strutture costituite da travi continue.Secondo il metodo delle forze, si assumono come incognite le reazioni dei vincoli sovrabbondanti, il cui numero è pari al grado di iperstaticità della struttura. Tali incognite si determinano attraverso la soluzione delle equazioni di congruenza, che impongono il rispetto delle condizioni cinematiche imposte dai vincoli soppressi.La struttura considerata, che è una trave su tre appoggi con grado di iperstaticità pari a 1, si rende isostatica sopprimendo il vincolo di continuità interna in corrispondenza dell’appoggio C e si assume come incognita iperstatica il corrispondente momento flettente MC.
-
Per l’analisi della struttura è conveniente sostituire la mensola AB con le azioni che essa trasmette all’appoggio B.
Risoluzione dello schema strutturale 2/8
-
2AB 1
Cs C BC C 1C C
C 2C C
32BC
BCC
2 2 21 2AB 1 AB 1 2 AB 1 2
C 1 1
( ) ( ) ( )2
( )3
( )24
2 2 6 12 6
p
pp p
q LM q F L
M LMEI
q Lq
EIF L Lq L q L L q L LF L F L
EI EI EI
φ φ φ φ
φ
φ
φ
= − + − +
=
=
⋅⎛ ⎞ ⎛ ⎞+ = + × = +⎜ ⎟ ⎜ ⎟⎝ ⎠ ⎝ ⎠
L’incognita MC viene determinata mediante la seguente equazione di congruenza
che impone l’uguaglianza delle rotazioni a destra e a sinistra dell’appoggio C, come imponeva il vincolo di continuità soppresso.Si ha:
C C CDCd C
3CD 3
CDC
33C
C C
( ) ( )
( )24
( )3
M q
q LqEI
M LM
EI
φ φ φ
φ
φ
= −
=
=
ΔφC = φCs −φCd = 0
Risoluzione dello schema strutturale 3/8
-
3 22 1 2C 2 AB 1 2BC
Cs
33 CD 3C
Cd
3 24 12 6
3 24
pq L F L LM L q L LEI EI EI EI
M L q LEI EI
φ
φ
⋅⋅= − + − +
= −
Risulta quindi:
da cui si ottiene la seguente equazione di congruenza:
che risolta fornisce:
3 2 32 31 2C 2 AB 1 2 CD 3BC C
C
3 24 12 6 3 24
17.70 kN m
pq L M LF L LM L q L L q LEI EI EI EI EI EI
M
⋅⋅− + − + = −
= ⋅
Risoluzione dello schema strutturale 4/8
-
BC 2 B C
2 2
2 1C 2 BC AB p 1 C
0
02 2
q L T TL L
T L q q F L M
− − =⎧⎪⎨
− + + − =⎪⎩
Calcolo dello sforzo di taglio nella campata BC
Imponendo l’equilibro alla traslazione verticale e alla rotazione intorno al punto B, si ha:
TB = 21,2 kNTC = 27,6 kN
⎧⎨⎪
⎩⎪
Risoluzione dello schema strutturale 5/8
-
Mmax=M (1.86) = − 2.6 ⋅1.7
2
2−0.1⋅1.7+ 21.2 ⋅1.86−11.35⋅1.86
2
2=16.1 kNm
Calcolo del momento massimo nella campata BC
Leggi di variazione del taglio e del momento
Ascissa di taglio nullo
Momento flettente massimo
TB − qBCx = 0
M (x) = − qABL12
2− FpL1 +TBx −
qBCx2
2
x =TBqBC
=1.86 m
Risoluzione dello schema strutturale 6/8
-
C CD 3 D
2
3D 3 C CD
0
02
T q L TL
T L M q
− + =⎧⎪⎨
+ − =⎪⎩
Calcolo dello sforzo di taglio nella campata CD
Imponendo l’equilibro alla traslazione verticale e alla rotazione intorno al punto C, si ha:
TC =11,6 kNTD = 5,2 kN
⎧⎨⎪
⎩⎪
Risoluzione dello schema strutturale 7/8
-
Mmax=M (3.80) = −17.7− 3.05⋅3.80
2
2+11.6 ⋅3.80 = 4.6 kNm
Risoluzione dello schema strutturale 8/8
Calcolo del momento massimo nella campata CD
Leggi di variazione del taglio e del momento
Ascissa di taglio nullo
Momento flettente massimo
TC − qCDx = 0
M (x) = −MC−qCDx
2
2+TCx
x = 11.63.05
= 3.80 m
-
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 1/10
Combinazione di carico 1 - Diagramma del momento flettente
-
Combinazione di carico 1 - Diagramma dello sforzo di taglio
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 2/10
-
Combinazione di carico 2 - Diagramma del momento flettente
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 3/10
-
Combinazione di carico 2 - Diagramma dello sforzo di taglio
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 4/10
-
Combinazione di carico 3 - Diagramma del momento flettente
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 5/10
-
Combinazione di carico 3 - Diagramma dello sforzo di taglio
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 6/10
-
Sovrapposizione dei diagrammi del momento flettente.
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 7/10
-
Inviluppo dei diagrammi del momento flettente.
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 8/10
-
Sovrapposizione dei diagrammi dello sforzo di taglio.
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 9/10
-
Inviluppo dei diagrammi dello sforzo di taglio.
Tracciamento dei diagrammi del momento e del taglio e del loro inviluppo 10/10
-
Progetto delle armature longitudinali 1/4
In una generica sezione, l’area minima dell’armatura, Asmin, viene calcolata con la relazione:
con:– MSd, momento flettente di calcolo– d, altezza utile della sezione (200 mm)– fyd, resistenza di calcolo dell’acciaio (391,3 MPa)
In ogni caso, il valore minimo deve rispettare l’indicazione della normativa che al punto 4.1.6.1.1 ne fornisce il seguente valore:
Al di fuori delle zone di sovrapposizione, inoltre, l’armatura tesa non deve superare il 4% dell’area del calcestruzzo.
Asn = 0.26 ⋅
fctmf yk
⋅b0 ⋅d ≤ 0.0013⋅b0 ⋅d
Asmin =
MSd0.9 ⋅d ⋅ f yd
-
Progetto delle armature longitudinali 2/4
Osservazioni
– La lunghezza massima delle barre è di 12 m– E’ opportuno impiegare non più di due diametri di armatura– E’ obbligatorio disporre inferiormente almeno una barra per travetto– Il numero massimo di barre da disporre superiormente non deve essere superiore a due– Il numero massimo di barre da disporre inferiormente non deve essere superiore a tre
-
Progetto delle armature longitudinali 3/4
Calcolata l’area strettamente necessaria, Asmin, bisogna stabilire il numero di barre da impiegare e il loro diametro.
Per le barre maggiormente utilizzate, la corrispondenza tra diametro e area della sezione è indicata nella seguente tabella.
ϕ [mm]
As
[mm2]
8 5010 7912 11314 154
-
Progetto delle armature longitudinali 4/4
Sezione MSd [kNm]d
[mm]Asmin
[mm2]Asmin
per travetto [mm2]
ϕϕϕ[mm]
As [mm2]
Appoggio B − 17.70 160 314 157 2ϕ10 158
Appoggio C − 34.70 200 493 246 2ϕ10 +1ϕ14 312
Campata BC 16.10 200 228 114 2ϕ10 158
Campata CD 32.10 200 456 228 2ϕ10 +1ϕ14 312
Nella seguente tabella si riporta l’armatura per travetto calcolata nelle sezioni più sollecitate. L’area minima è stata suddivisa per ogni travetto, considerando che l’analisi è stata eseguita per una fascia di larghezza pari a 1.0 m, e che in tale fascia sono contenuti due travetti.
-
Dopo avere progettato le armature, si calcola il momento resistente dell’acciaio e quello del calcestruzzo.
Momento resistente dell’acciaioIl momento resistente dell’acciaio si calcola con la relazione
Nel caso in esame si ha:
ϕ [mm]
d[mm]
As per travetto
[mm2]
As per metro
[mm2]
fyd[N/mm2]
MRsd per metro
[kNm]10 160 79 158 391.3 17.8010 200 79 158 391.3 22.2614 200 154 308 391.3 43.95
MRsd = 0.9 ⋅d ⋅ As ⋅ f yd
Calcolo del momento resistente 1/5
-
La presenta tabella mostra che nelle sezioni più sollecitate il momento resistente dell’acciaio, MRsd, è sempre maggiore in valore assoluto del momento agente di calcolo, MSd (i valori dei momenti si riferiscono a una fascia di solaio larga un metro).
Calcolo del momento resistente 2/5
Sezione MSd [kNm]d
[mm]ϕ
[mm] MRsd
[kNm]
Appoggio B − 17.70 160 2ϕ10 − 17.80
Appoggio C − 34.70 200 2ϕ10 +1ϕ14 − 43.95
Campata BC 16.10 200 2ϕ10 22.26
Campata CD 32.10 200 2ϕ10 +1ϕ14 43.95
-
Momento resistente del calcestruzzoIl momento resistente del calcestruzzo è stato calcolato considerando una larghezza b0 della sezione pari a 10 cm nel caso del travetto, a 30 cm nel caso di fascia semipiena e a 50 cm nel caso di fascia piena.
Appoggio Fascia semipiena Fascia piena
Calcolo del momento resistente 4/5
-
Il momento resistente del calcestruzzo si determina invertendo la formula di progetto. Si ha:
in cui, supponendo presente un’armatura compressa minima, si ponePer una fascia di 1.0 metro, nei tre casi di (a) travetti, (b) fascia semipiena e (c) fascia piena si ha:
M Rcd =
b0d2
′r 2
MRcd = 2
0.10 ⋅0.202
0.0182= 24.70 kNm
Calcolo del momento resistente 3/5
′r 2 = 0.018.
MRcd = 2
0.10 ⋅0.162
0.0182=15.80 kNm
MRcd = 2
0.30 ⋅0.202
0.0182= 74.08 kNm
MRcd = 2
0.30 ⋅0.162
0.0182= 47.40 kNm
MRcd = 2
0.50 ⋅0.202
0.0182= 123.46 kNm
MRcd = 2
0.50 ⋅0.162
0.0182= 79.02 kNm
d = 160 mm (sbalzo) d = 200 mm (campate)
(a)
(b)
(c)
-
Per le sezioni più sollecitate, nella seguente tabella sono riportati a confronto i valori dei momenti resistenti del calcestruzzo con quelli di calcolo (fascia di solaio larga un metro).
Si nota che il momento flettente negativo agente sugli appoggi è spesso maggiore diquello resistente dei travetti, ma inferiore a quello relativo alla fascia semipiena. Sono quindi necessarie fasce semipiene in prossimità degli appoggi, la cui ampiezza si ottiene graficamente imponendo che il diagramma del momento resistente del calcestruzzo sia sempre esternoall’inviluppo dei diagrammi del momento flettente.
Calcolo del momento resistente 5/5
Sezione MSd [kNm]d
[mm]
MRcd [kNm]
travetto fascia semipienafascia piena
Appoggio B − 17.70 160 − 15.80 − 47.40
Appoggio B − 17.70 200 − 24.70
Appoggio C − 34.70 200 − 24.70 − 74.08
Campata BC 16.10 200 123.46
Campata CD 32.10 200 123.46
-
Diagramma del momento resistente
Stabilito il diametro e il numero di barre da impiegare, occorre disporre l’armatura all’interno dei travetti. Quest’operazione si può eseguire graficamente dopo avere costruito il diagramma dei momenti resistenti, che deve essere sempre esterno all’inviluppo dei diagrammi del momento flettente.
F6.6 kNm
B
2 10Mrd = 11 kN m
8.05 kNm
2 10Mrd = 11 kN m
C
17..35 kNm
16.05 kNm
D
1 10Mrd = 4.4 kN m
8.85 kNm
2 10 + 1 14Mrd = 21.8 kN m
A
2 10 + 1 14Mrd = 21.8 kN m
2 Ф10 Mrd = 11 kNm
1 Ф10 Mrd = 4.4 kNm
2 Ф10 Mrd = 11 kNm
2 Ф10+1 Ф14 Mrd = 21.8 kNm
2 Ф10+1 Ф14 Mrd = 21.8 kNm
-
È importante sottolineare che le armature devono essere convenientemente ancorate. In accordo con le NTC08, la lunghezza d’ancoraggio può essere convenzionalmente assunta pari a 40 ϕ.
Distinta delle armature
40
15200
L2 = 4.3 m
15
40
1 10 L= 230 15 2 10+ 1 14 L=805
2 10+1 14 L=615
545
29315
15
L1 = 1.7 m
2 10 L= 348
L3 = 5.5 m
2 10 L=600 560
40
15
750
1 Ф10 2 Ф10
1 Ф10
-
Poiché nei travetti del solaio non si dispone l’armatura trasversale, la sollecitazione di taglio deve essere interamente assorbita dal calcestruzzo.La verifica deve essere eseguita in corrispondenza degli appoggi, dove lo sforzo di taglio raggiunge i valori massimi. A tale proposito e con riferimento a un singolo travetto, si considera il seguente inviluppo dei diagrammi degli sforzi di taglio, relativi a tutte le combinazioni di carico considerate.
Verifiche allo stato limite ultimo per le sollecitazioni di taglio 1/8
-
Il valore del taglio resistente di calcolo di un travetto, VRd, si ricava attraverso la relazione:
dove
La verifica si conduce confrontando il valore del taglio resistente con lo sforzo di taglio agente in corrispondenza degli appoggi (taglio di calcolo).
VRd =0.18 ⋅ k ⋅ 100 ⋅ρ1 ⋅ fck( )1/3
γ c+ 0.15⋅σ cp
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥b0 ⋅d
k =1+ 200 / d ≤ 2, in cui d = 200 mm l'altezza utile della sezione
ρ1 =
Asb0d
è la percentuale geometrica di armatura longitudinale tesa
σ cp =
NsdAc
è la tensione media di compressione della sezione (in MPa)
fck è la resistenza caratteristica cilindrica a compressione del calcestruzzo (in MPa)
γ c = 1.5 è il coefficiente di sicurezza parziale del calcestruzzo
Verifiche allo stato limite ultimo per le sollecitazioni di taglio 2/8
-
Il taglio resistente viene calcolato considerando una larghezza b0 della sezione pari a 10 cm nel caso del travetto, a 30 cm nel caso di fascia semipiena e a 50 cm nel caso di fascia piena.
Appoggio Fascia semipiena Fascia piena
Verifiche allo stato limite ultimo per le sollecitazioni di taglio 3/8
-
Appoggio B Il taglio massimo di calcolo è pari a VSd = 10.60 kN. Poiché risulta
il taglio resistente vale
b0 = 10 cm – Travetto
b0 = 30 cm – Fascia semipiena
b0 = 50 cm – Fascia piena
Si nota che il valore del taglio resistente calcolato per b0 = 10 cm è maggiore del taglio di calcolo massimo VSd = 10.60 kN. Non è pertanto necessario realizzare fasce piene o semipiene.
k =1+ 200 / 200 = 2.00
ρ1 =
158100 ⋅200
= 0.0079
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0079 ⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥100 ⋅200 ⋅10−3 = 12.97 kN
ρ1 =
158300 ⋅200
= 0.0026
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0026 ⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥300 ⋅200 ⋅10−3 = 26.87 kN
ρ1 =
158500 ⋅200
= 0.0016
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0016 ⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥500 ⋅200 ⋅10−3 = 38.09 kN
Verifiche allo stato limite ultimo per le sollecitazioni di taglio 4/8
-
Appoggio C Il taglio massimo di calcolo è pari a VSd = 18.75 kN. Poiché risulta
il taglio resistente vale
b0 = 10 cm – Travetto
b0 = 30 cm – Fascia semipiena
b0 = 50 cm – Fascia piena
Si nota che il valore del taglio resistente calcolato per b0 = 10 cm è inferiore al taglio di calcolo massimo VSd = 18.75 kN. È pertanto necessario realizzare una fascia semipiena a destra dell’appoggio.
k =1+ 200 / 200 = 2.00
ρ1 =
312100 ⋅200
= 0.0156
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0156 ⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥100 ⋅200 ⋅10−3 = 16.28 kN
ρ1 =
312300 ⋅200
= 0.0052
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0052 ⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥300 ⋅200 ⋅10−3 = 33.85 kN
ρ1 =
312500 ⋅200
= 0.0031
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0031⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥500 ⋅200 ⋅10−3 = 47.49 kN
Verifiche allo stato limite ultimo per le sollecitazioni di taglio 5/8
-
Appoggio D Il taglio massimo di calcolo è pari a VSd = 13.50 kN. Poiché risulta
il taglio resistente vale
b0 = 10 cm – Travetto
b0 = 30 cm – Fascia semipiena
b0 = 50 cm – Fascia piena
Si nota che il valore del taglio resistente calcolato per b0 = 10 cm è inferiore al taglio di calcolo massimo VSd = 13.50 kN. È pertanto necessario realizzare una fascia semipiena a sinistra dell’appoggio.
k =1+ 200 / 200 = 2.00
ρ1 =
79100 ⋅200
= 0.0040
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0040 ⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥100 ⋅200 ⋅10−3 = 10.34 kN
ρ1 =
79300 ⋅200
= 0.0013
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0013⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥300 ⋅200 ⋅10−3 = 21.33 kN
ρ1 =
79500 ⋅200
= 0.0008
VRd =0.18 ⋅2.00 ⋅ 100 ⋅0.0008 ⋅25( )1/3
1.5
⎡
⎣
⎢⎢
⎤
⎦
⎥⎥500 ⋅200 ⋅10−3 = 30.24 kN
Verifiche allo stato limite ultimo per le sollecitazioni di taglio 6/8
-
Verifiche allo stato limite ultimo per le sollecitazioni di taglio 7/8
Appoggio VSd [kN]VRd [kN]
b0 = 10 cmVRd [kN]
b0 = 30 cmVRd [kN]
b0 = 50 cm
B 10.60 12.97 26.87 38.09C 18.75 16.28 33.85 47.49D 13.50 10.34 21.33 30.24
Tabella riassuntiva
-
Verifiche allo stato limite ultimo per le sollecitazioni di taglio 8/8
Diagramma del taglio resistente e fasce semipieneImpossibile visualizzare l'immagine. La memoria del computer potrebbe essere insufficiente per aprire l'immagine oppure l'immagine potrebbe essere danneggiata. Riavviare il computer e aprire di nuovo il file. Se viene visualizzata di nuovo la x rossa, potrebbe essere necessario eliminare l'immagine e inserirla di nuovo.Impossibile visualizzare l'immagine. La memoria del computer potrebbe essere insufficiente per aprire l'immagine oppure l'immagine potrebbe essere danneggiata. Riavviare il computer e aprire di nuovo il file. Se viene visualizzata di nuovo la x rossa, potrebbe essere necessario eliminare l'immagine e inserirla di nuovo.