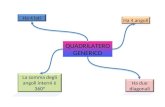
Volume VI - Diretto€¦ · lunghezza pari a 5 cm: potrebbe essere un rombo, ma anche un quadrato....

Leonardo Tortorelli

CORSO DI GEOMETRIA VERTICALE

Volume VI

TEORIA DEI QUADRILATERI

IIVV TTOORRNNEEOO NNAAZZIIOONNAALLEE DDII

Geometriko Versione 4.9.01

DOCENTI SCUOLA PRIMARIA (G1)

DOCENTI SCUOLA SECONDARIA DI 1° GRADO (G2)

STUDENTI SCUOLA SECONDARIA DI 1° GRADO (G2)

STUDENTI SCUOLA SECONDARIA DI 2° GRADO (G3)

Estratto da “Corso di Geometria Verticale – Volume VI” © Leonardo Tortorelli - 2017

2

Leonardo Tortorelli

CORSO DI

GEOMETRIA VERTICALE

Volume VI

TEORIA DEI QUADRILATERI Programma sintetico di Geometria Euclidea

finalizzato all’ottimizzazione

del modello didattico Geometriko

CORSO DI GEOMETRIA A LIVELLI PER

DOCENTI DELLA SCUOLA PRIMARIA

STUDENTI E DOCENTI

DELLA SECONDARIA DI I / II GRADO


3

GGGeeeooommmeeetttrrriiikkkooo 444...999...000111 (((AAAggggggiiiooorrrnnnaaammmeeennntttooo 222555 NNNooovvveeemmmbbbrrreee 222000111888)))

Leonardo Tortorelli

La presente Dispensa di Gioco di Geometriko sostituisce a livello ufficiale quella presente sulla versione

―Geometriko 3.0‖ (stampata a Marzo 2017 da Edizioni Erickson, Trento). Questo elaborato unitamente ai

successivi aggiornamenti sarà ritenuto il documento ufficiale teorico utilizzato per tutto il IV Torneo Nazionale

di Geometriko.

IMPORTANTE

La presente dispensa è destinata ai docenti della Scuola Primaria che utilizzeranno per i propri alunni la

versione Geometriko Junior.

La presente dispensa è anche destinata agli alunni della Scuola Secondaria di 1° Grado e contiene tutte le

possibili conoscenze per formulare domande utilizzabili con la flash card ―CAPRONE UGO‖.


4

Progettazione/Editing

Leonardo Tortorelli

Grafica e impaginazione

Leonardo Tortorelli

Copertina

© Leonardo Tortorelli © 2017 Leonardo Tortorelli

Tel. 320 674 3350

ISBN: XXX-XX-XXX-XXXX-X (in attesa di assegnazione)

Tutti i diritti riservati. Vietata la riproduzione con qualsiasi mezzo effettuata, se non previa autorizzazione dell’Autore.

È consentita la fotocopiatura dell’opera e la distribuzione degli e-book a esclusivo uso didattico interno all’istituto.

Finito di stampare nel mese di gennaio 2018

da Tipografia Handmade – Lecce (LE)


5

TEORIA DEI QUADRILATERI ...................................................................................................................... 7

06.01 – Generalità sui Quadrilateri .................................................................................................. 7 06.01.a) Definizione (Quadrilateri) ................................................................................................ 7 06.01.b) Definizione (Quadrilatero Scaleno) ................................................................................. 7 06.01.c) Definizione (Quadrilateri Concavi e Convessi) ................................................................ 7 06.01.d) Proprietà di un Quadrilaterio Generico ............................................................................. 8

06.01.e) Osservazione ..................................................................................................................... 8 06.02 – Il Trapezio ........................................................................................................................... 8

06.02.a) Definizione (Trapezio) ...................................................................................................... 8 06.02.b) Definizione (Trapezio Rettangolo) ................................................................................... 9 06.02.c) Osservazioni sul Trapezio Rettangolo ............................................................................... 9

06.02.d) Definizione (Trapezio Isoscele) ...................................................................................... 10

06.02.e) Teorema sui Lateral Sides di un Trapezio Isoscele ......................................................... 10 06.02.h) Definizione (Trapezio Scaleno) ...................................................................................... 10

06.02.g) Teorema sugli Angoli dei Trapezi Isosceli ..................................................................... 10 06.02.h) Teorema sulle Diagonali dei Trapezi Isosceli ................................................................. 10 06.02.i) Calcolo dell’Area di un Trapezio .................................................................................... 11

06.02.j) Osservazione (Didattica) ................................................................................................... 11 06.02.k) Osservazione (Didattica) .................................................................................................. 11

06.03 – Aquilone, Deltoide o Kite ................................................................................................. 12

06.03.a) Definizione (Aquilone/Deltoide/Kite) ............................................................................. 12 06.03.b) Teorema (Diagonali dell’Aquilone) ................................................................................ 12

06.03.c) Teorema (Angoli Congruenti di un Aquilone) ................................................................ 12 06.03.d) Teorema (Asse di Simmetria di un Aquilone) ................................................................ 12

06.04 – Il Parallelogramma ............................................................................................................ 13

06.04.a) Definizione (Parallelogramma) ....................................................................................... 13

06.04.b) Altezze del Parallelogramma .......................................................................................... 13 06.04.c) Primo Teorema dei Parallelogrammi ............................................................................... 14 06.04.d) Secondo Teorema dei Parallelogrammi ........................................................................... 14 06.04.e) Terzo Teorema dei Parallelogrammi ............................................................................... 14

06.04.f) Definizione (Romboide) .................................................................................................. 15 06.04.g) Definizione (Quadrilatero di Varignon) .......................................................................... 15 06.04.h) Area del Quadrilatero di Varignon .................................................................................. 16 06.04.i) Calcolo dell’Area di un Parallelogramma ....................................................................... 16

06.05 – Il Rettangolo ...................................................................................................................... 16

06.05.a) Definizione (Rettangolo) ................................................................................................. 16 06.05.b) Teorema .......................................................................................................................... 17 06.05.c) Teorema ........................................................................................................................... 17 06.05.d) Teorema .......................................................................................................................... 17 06.05.e) Teorema ........................................................................................................................... 17

06.05.f) Teorema ........................................................................................................................... 17 06.05.g) Calcolo dell’Area di un Rettangolo ............................................................................... 18

06.05.i) Un rettangolo speciale: il Rettangolo Tatami ................................................................. 18 Il Tatami ......................................................................................................................................... 18 Il Tatami come Unità di Misura / Misure Standard del Tatami ..................................................... 19 Definizione (Rettangolo Tatami) .................................................................................................... 19 Tatami Room Patterns .................................................................................................................... 19

06.06 – Il Rombo ........................................................................................................................... 20


6

06.06.a) Definizione (Rombo) ....................................................................................................... 20

06.06.b) Teorema .......................................................................................................................... 20 06.06.c) Primo Teorema sulle Diagonali del Rombo .................................................................... 20 06.06.d) Secondo Teorema sulle Diagonali del Rombo ................................................................ 20 06.06.e) Calcolo dell’Area di un Rombo ..................................................................................... 21

06.07 – Il Quadrato ........................................................................................................................ 21

06.07.a) Definizione (Quadrato) ................................................................................................... 21 06.07.b) Teorema .......................................................................................................................... 21 06.07.c) Teorema ........................................................................................................................... 21 06.07.d) Teorema .......................................................................................................................... 22 06.07.e) Teorema ........................................................................................................................... 22

06.07.f) Calcolo dell’Area di un Quadrato ................................................................................... 22 06.08 – Quadrilateri Simili ............................................................................................................ 23

06.08.a) Definizione di Quadrilateri Simili .................................................................................. 23

06.08.b) Teorema (Perimetro di Figure Simili) ............................................................................ 23 06.08.c) Teorema (Area di Figure Simili) .................................................................................... 23 06.08.d) Misconcezione Frequente sulla Definizione di Similitudine ......................................... 23

06.09 – Quadrilateri Isoperimetrici ................................................................................................ 24 06.09.a) Definizione (Figure Isoperimetriche) ............................................................................ 24 06.09.b) Definizione (Quadrilateri Isoperimetrici) ...................................................................... 24

06.09.c) Osservazione .................................................................................................................. 24 06.10 – Quadrilateri Equiestesi ...................................................................................................... 24

06.10.a) Definizione (Superfici Equiestese/Equivalenti) ............................................................ 24 06.10.b) Definizione (Quadrilateri Equiestesi/Equivalenti) ......................................................... 24 06.10.c) Osservazione .................................................................................................................. 25

LEGENDA DEI SIMBOLI UTILIZZATI

SIMBOLI MATEMATICI

: Simbolo di Parallelismo tr (leggi: a Rette Paral a )lel//

: Simbolo di Perpendicolarità tra Rette Perpendicolare Ortogonale(leggi: , )

: Simbolo di Congruenza tra Figure (leggi: Geometriche Congru e )ent

: Simbolo di Equiestenione tra Figure Geometriche Equiestes (leg a Equivalentegi: , )

: Simbolo di Coincidenza tra Figure (leggi Geome : triche Coin e )cid


7

“CORSO DI GEOMETRIA VERTICALE”

Volume VI

TEORIA DEI QUADRILATERI

06.01 – Generalità sui Quadrilateri

06.01.a) Definizione (Quadrilateri)

Si definisce Quadrilatero un qualunque poligono avente quattro lati.

In tale figura le misure dei quattro lati – come si vedrà nel [§06.01.d / Proprietà III] – non sono

assolutamente casuali, ma tra loro sussiste una particolare relazione.

06.01.b) Definizione (Quadrilatero Scaleno)

Si definisce Quadrilatero Scaleno un quadrilatero che non ha né angoli né lati

congruenti.

06.01.c) Definizione (Quadrilateri Concavi e Convessi)

I quadrilateri possono essere concavi o convessi. Si definisce Quadrilatero Convesso un

quadrilatero tale che per ogni coppia di punti interni il segmento che li congiunge è formato da

punti tutti interni al quadrilatero. Se questa proprietà non si verifica, il quadrilatero si definisce

Quadrilatero Concavo.


8

06.01.d) Proprietà di un Quadrilaterio Generico

I) La somma degli angoli interni di un quadrilatero misura 360°.

II) Ogni quadrilatero ha due diagonali. Se il quadrilatero è convesso e il loro punto di intersezione è

centro di simmetria, esso si definisce Centro del Quadrilatero.

III) La lunghezza di ciascun lato è minore della somma delle lunghezze degli altri tre lati.

06.01.e) Osservazione

Assegnate le misure di tutti i lati, un quadrilatero non è univocamente determinato (perché variano

le ampiezze degli angoli e la successione dei lati).

Un esempio plateale per convincersi di ciò è pensare a un quadrilatero equilatero con lato avente

lunghezza pari a 5 cm: potrebbe essere un rombo, ma anche un quadrato.

06.02 – Il Trapezio

06.02.a) Definizione (Trapezio)

Si definisce Trapezio un quadrilatero che ha (almeno) una coppia di lati paralleli.

Dato un trapezio, si definiscono:

– Basi del Trapezio i lati paralleli del trapezio;

– Lateral Sides, gli altri due lati non considerati come basi (su altri testi anche denominati Lati

Obliqui o Lati del Trapezio).

– Altezze del Trapezio, tutti i segmenti compresi tra le due rette contenenti le basi e a esse

perpendicolari. Si hanno quindi infinite altezze. Si ha l’unicità dell’altezza solo quando essa è

riferita a un lato e a un determinato vertice (si ricordi che per un punto passa una e una sola

perpendicolare a una retta data).


9

Nella precedente immagine i segmenti EF, DH, GI, CK, JL, MN sono altezze del trapezio. Le altezze del

trapezio sono dunque infinite. Per individuare univocamente una di esse è necessario fare riferimento a un

lato e a un determinato punto; ad esempio, per indicare le altezze più ―famose‖ DH e CK si dirà

rispettivamente: ―Si consideri l’altezza del trapezio condotta dal vertice D relativamente alla base AB‖ e ―Si

consideri l’altezza del trapezio condotta dal vertice C relativamente alla base AB‖.

06.02.b) Definizione (Trapezio Rettangolo)

Si definisce Trapezio Rettangolo un trapezio con almeno due lati perpendicolari.

06.02.c) Osservazioni sul Trapezio Rettangolo

I) Un trapezio rettangolo ha almeno due angoli retti.

II) In un trapezio rettangolo almeno una delle infinite altezze relativa alle basi coincide con uno dei

lati del trapezio.

- Quanti lati coincidenti con le altezze può al massimo avere un trapezio rettangolo?

- Generalmente un’altezza coincide con un lato, potrebbe però accadere che il trapezio rettangolo

sia un rettangolo e che dunque, i lati che coincidono con le altezze riferite a due basi prefissate,

diventino due.


10

06.02.d) Definizione (Trapezio Isoscele)

Si definisce Trapezio Isoscele un quadrilatero con

almeno due lati paralleli e gli angoli adiacenti a uno

di essi congruenti.

06.02.e) Teorema sui Lateral Sides di un Trapezio Isoscele

Se un trapezio è un trapezio isoscele allora ha i lateral sides

congruenti.

- Per questo teorema non vale il viceversa! Saresti in grado di fornire un controesempio (cioè un esempio

di trapezio avente i lateral sides congruenti che non sia un trapezio isoscele)?

- Basta considerare un parallelogramma (che non sia un rettangolo), infatti esso ha… ma non è un…

06.02.h) Definizione (Trapezio Scaleno)

Si definisce Trapezio Scaleno un trapezio non isoscele.

06.02.g) Teorema sugli Angoli dei Trapezi Isosceli

Un quadrilatero è un trapezio isoscele se e soltanto se

esistono almeno due lati opposti tali che gli angoli

adiacenti a ciascuno di essi sono tra loro congruenti.

06.02.h) Teorema sulle Diagonali dei Trapezi Isosceli

Un trapezio è isoscele se e soltanto se ha le diagonali

congruenti.


11

06.02.i) Calcolo dell’Area di un Trapezio

Dato un trapezio, si considerino:

due sue basi aventi lunghezza rispettivamente b1 e b2;

un’altezza relativa alle basi considerate avente lunghezza h.

L’area del trapezio vale:

[(Somma delle Lunghezze delle Basi)] (Lunghezza Altezza Relativa alle Basi)

=

2TrapezioArea

Cioè, in linguaggio simbolico:

( )

=2

Trapezio

b +b hArea

1 2

06.02.j) Osservazione (Didattica)

Corretto utilizzo dei termini lati obliqui, base maggiore e base minore.

- Nella scuola primaria e talvolta anche nella secondaria di primo grado, tali nomenclature sono

sconsigliabili dal punto di vista didattico a causa del conflitto cognitivo che sopravviene quando

si osserva che rettangoli e quadrati sono anche trapezi. Lo studente (e non solo), in tali casi,

incontra difficoltà perché: non vede né i lati obliqui (in senso letterale), né una base maggiore né

una base minore, ma ben due coppie di basi costituite da lati opposti aventi la stessa lunghezza!

Per poter mantenere includere tali casi particolari anche nel primo ciclo - mantenendo tali

tradizionali nomi a cui tutti sono ―affezionati‖ - dovremmo chiamarle, più rigorosamente, ―base

maggiore o uguale‖ e ―base minore o uguale‖.

- Nella secondaria di secondo grado, invece, è bene utilizzare i termini lati obliqui, base maggiore

e base minore, in quanto, è una bella occasione per affrontare il discorso dei ―casi limite‖ e delle

―figure degeneri‖.

06.02.k) Osservazione (Didattica)

Considerato un qualunque lato di un trapezio, quelle di essere base e/o lateral side sono proprietà

che non dipendono da come il trapezio si colloca nel piano (ad esempio da come è disegnato sul

foglio) ma solo dalle relazioni tra i suoi lati.


12

06.03 – Aquilone, Deltoide o Kite

06.03.a) Definizione (Aquilone/Deltoide/Kite)

Si definisce Aquilone o Deltoide o Kite un quadrilatero in cui ci sono

due lati consecutivi congruenti e gli altri due sono a loro volta tra loro

congruenti.

Curiosità / Tale nome deriva dalla lingua tedesca, in cui si usa deltoide

come sostantivo maschile sinonimo di aquilone.

Attenzione a non confondere il deltoide con il romboide che sarà

definito nei prossimi paragrafi, ma noi, chiamandolo aquilone questo

rischio non lo correremo affatto!

La recente tendenza è quella di non utilizzare il nome deltoide, in

quanto, con la parola deltoide si denota prioritariamente una curva piana detta anche Tricuspoide

(studiata per la prima volta da Eulero). Kite - che in inglese vuol dire ancora una volta aquilone - è

il nome più utilizzato in ambito internazionale per denotare questo quadrilatero.

06.03.b) Teorema (Diagonali dell’Aquilone)

L’aquilone ha le diagonali perpendicolari.

06.03.c) Teorema (Angoli Congruenti di un Aquilone)

L’aquilone ha almeno una coppia di angoli opposti congruenti.

Tali angoli sono quelli aventi come vertici i punti comuni a due lati

aventi lunghezza diversa (salvo eccezioni tipo il rombo dove si hanno tutti i lati congruenti).

06.03.d) Teorema (Asse di Simmetria di un Aquilone)

La retta passante per la diagonale che collega i due vertici opposti comuni alle due coppie di lati

congruenti è asse di simmetria per l’aquilone.


13

06.04 – Il Parallelogramma

06.04.a) Definizione (Parallelogramma)

Si definisce Parallelogramma un quadrilatero avente i lati opposti paralleli.

Nella seguente immagine, con M, è indicato il Centro del Parallelogramma (definito in generale

nel paragrafo [§06.01(d)_II]).

In base alla sua definizione ogni parallelogramma è un trapezio e quindi l’insieme dei

parallelogrammi è un sottoinsieme dell’insieme dei trapezi.

Curiosità / si può dire indifferentemente sia «parallelogramma», sia «parallelogrammo».

06.04.b) Altezze del Parallelogramma

Come per tutti i quadrilateri anche in questo caso

si hanno infinite altezze. Si ha l’unicità

dell’altezza solo quando essa è riferita a un lato e

a un vertice ben determinati (si ricordi che per

un punto passa una e una sola perpendicolare a

una retta data).

Ad esempio, il segmento, DH è l’unica altezza

condotta dal vertice D relativamente al lato AB e

CK l’unica altezza condotta dal vertice C relativamente al lato AD.

Da ogni vertice è possibile condurre due altezze relativamente ai due lati opposti.


14

- Quante sono in totale le altezze condotte dai quattro vertici relativamente ai quattro lati del

parallelogramma? Disegnale tutte!

- Risposta: le altezze che è possibile disegnare in totale sono due per ciascuno dei quattro vertici

per un totale di otto altezze. Si consiglia vivamente di disegnarle perché è un esercizio tutt’altro

che inutile.

06.04.c) Primo Teorema dei Parallelogrammi

Un quadrilatero è un parallelogramma se e soltanto se i lati opposti sono congruenti.

06.04.d) Secondo Teorema dei Parallelogrammi

Un quadrilatero è un parallelogramma se e soltanto se gli angoli opposti sono congruenti.

06.04.e) Terzo Teorema dei Parallelogrammi

Un quadrilatero è un parallelogramma se e soltanto se le diagonali s’intersecano nei loro punti

medi.


15

- Premessa / Le prime due condizioni necessarie e sufficienti espresse nelle pagine precedenti

richiedono che entrambe le coppie di lati opposti siano congruenti ed entrambe le coppie di

angoli opposti siano congruenti. Una sola coppia di lati (o di angoli) opposti congruenti non è

sufficiente a garantire che un quadrilatero sia un parallelogramma..

Fornire un esempio di un quadrilatero avente una coppia di lati opposti congruenti che non sia un

parallelogramma e un altro avente una coppia di angoli opposti congruenti che non sia un

parallelogramma.

- Risposta

Un esempio notevole di quadrilatero (non parallelogramma)

con una sola coppia di lati opposti congruenti è banalmente il

trapezio isoscele.

Un esempio di quadrilatero (non

parallelogramma) con una sola coppia di

angoli opposti congruenti è l’aquilone

convesso.

06.04.f) Definizione (Romboide)

Si definisce Romboide un parallelogramma che non ha né lati consecutivi congruenti né angoli

adiacenti congruenti.

Si definisce, pertanto, Romboide un parallelogramma senza:

- congruenze tra lati consecutivi (un rombo o un quadrato quindi, non sono romboidi);

- congruenze tra angoli ―consecutivi‖ (un rettangolo o un quadrato quindi, non sono romboidi).

06.04.g) Definizione (Quadrilatero di Varignon)

Dato un qualunque quadrilatero Q, si definisce Quadrilatero di

Varignon associato a Q il quadrilatero ottenuto congiungendo i

punti medi dei suoi lati.

Si dimostra che il Quadrilatero di Varignon è un parallelogramma.


16

06.04.h) Area del Quadrilatero di Varignon

Dato un quadrilatero convesso Q qualunque, denominato QV il suo Quadrilatero di Varignon,

risulta che l’area di quest’ultimo è la metà di quella dell’area di Q.


1( )

2( )VQ Area QArea

06.04.i) Calcolo dell’Area di un Parallelogramma

Dato un un parallelogramma, si consideri:

una qualsiasi delle sue quattro basi avente lunghezza b;

la lunghezza h delle altezze relative alla base considerata.

L’area del parallelogramma vale:

(Lunghezza di Una Base) (Lunghezza Altezza Relativa alla Base Scelta) ParallelogrammaArea


=Parallelogramma b hArea

Osservazione

Nei parallelelogrammi — che sono trapezi particolari — tutti i lati sono al contempo sia basi sia

lateral sides.

06.05 – Il Rettangolo

06.05.a) Definizione (Rettangolo)

Si definisce Rettangolo un quadrilatero avente tutti gli angoli congruenti.


Rettangolo ABCD


17

06.05.b) Teorema

Un quadrilatero è un rettangolo se e soltanto se ha tutti gli angoli retti.

06.05.c) Teorema

Tutti i rettangoli sono trapezi isosceli.

06.05.d) Teorema

Tutti i rettangoli sono parallelogrammi.

L’insieme dei rettangoli è quindi un sottoinsieme dell’insieme dei parallelogrammi.

Poiché ogni rettangolo è un parallelogramma, valgono per i rettangoli tutte le proprietà che valgono

per i parallelogrammi.

06.05.e) Teorema

Se un quadrilatero è un rettangolo allora ha le diagonali congruenti.

06.05.f) Teorema

Un quadrilatero è un rettangolo se e soltanto se è un parallelogramma avente le diagonali

congruenti.

N.B. Da essa si deduce che: un quadrilatero per essere un rettangolo deve intanto essere un

parallelogramma e poi verificare la condizione di congruenza delle sue diagonali. Attenzione

però, per un quadrilatero generico, il verificarsi della condizione di congruenza delle diagonali

è una condizione necessaria ma non sufficiente per concludere che esso sia un rettangolo.

Infatti, considerato ad esempio il quadrilatero in figura (che è un particolare aquilone), ha le

diagonali congruenti ma non è un rettangolo!


18

Conclusioni / Un quadrilatero con le diagonali congruenti è un

rettangolo solo se questo è già per ipotesi un parallelogramma,

mentre un quadrilatero generico con le diagonali congruenti non è

detto che lo sia, potrebbe essere ad esempio un trapezio isoscele

oppure un aquilone convesso particolare (aquilone convesso con

diagonali congruenti).

06.05.g) Calcolo dell’Area di un Rettangolo

Dato un rettangolo, si consideri:

una qualsiasi delle sue quattro basi avente lunghezza b;

la lunghezza h delle altezze relative alla base considerata.

Essendo il rettangolo un parallelogramma, la sua area vale:

Rettangolo = (Lunghezza di Una Base) (Lunghezza Altezza Relativa alla Base Scelta) Area


Rettangolo = b hArea

Osservazione

Nei rettangoli — che sono trapezi particolari — tutti i lati sono sia basi sia lateral sides.

06.05.i) Un rettangolo speciale: il Rettangolo Tatami

Il Tatami

Il Tatami (畳) è una tradizionale pavimentazione giapponese

composta da pannelli rettangolari modulari, costruiti con un

telaio di legno rivestito da paglia intrecciata e pressata.

Si usa il termine ―Tatami‖ per indicare sia il singolo tappeto solitamente

di forma rettangolare oppure quadrato (Mezzo Tatami), costruito in paglia

di riso intrecciata e pressata, sia il tradizionale pavimento giapponese

composto da più stuoie accostate l’una all’altra. Con il passare degli anni, i tatami, sono stati sempre più ricercati

anche nel mondo occidentale perché creano un ambiente ecosostenibile e privo di sostanze nocive, in quanto,

costituito solo da elementi prettamente naturali.

I bordi dei Tatami sono solitamente squadrati con grande

precisione e grazie a ciò esiste la possibilità di incastrarli alla

perfezione senza utilizzare collanti per fissarli al pavimento.

I tatami ―originali giapponesi‖ sono rivestiti da un doppio

strato di tessuto tipico giapponese molto simile all’erba del

prato. La paglia di riempimento, derivante dal riso, viene

naturalmente essiccata per un anno e cotta a temperature

molto elevate per rimuovere i parassiti e gli acari,

praticamente sterilizzandolo totalmente.


19

I tatami sono da alcuni secoli utilizzati

per ricoprire le stanze. Per tradizione sui

tatami si cammina soltanto a piedi nudi o

con delle calze.

Questo tipo di materiale è legato anche

alla cerimonia del tè, che si svolge con un

braciere poggiato o con la modifica di

una buca quadrata detta ―ro‖ fatta a uno

dei tatami, attorniata da una cornice

laccata, detta ―robuchi‖.

Oggi, nelle discipline sportive come ad

esempio il Judo, il tatami è usato come

materasso su cui è possibile cadere senza

riportare traumi. Nelle discipline sportive quindi con il termine tatami si indicano i materassini su cui poter

svolgere l’attività, in quanto, assorbono gli urti, motivo per cui sono eccellenti durante la pratica delle arti

marziali, ma anche per l’uso domestico, soprattutto bambini e anziani potranno beneficiare delle caratteristiche

ammortizzanti ed antitrauma di questa specifica attrezzatura.

Il Tatami come Unità di Misura / Misure Standard del Tatami

Il ―Tatami‖ viene usato come unità di misura per indicare le dimensioni degli ambienti e può anche

avere diversi spessori che di norma raggiungono i 6 cm. Orientativamente il tatami è lo spazio

occupato da una persona sdraiata. Le misure più frequenti sono:

Tatami ( 90 cm × 180 cm ) o ( 95 cm × 190 cm )

Mezzo Tatami ( 90 cm × 90 cm ) o ( 95 cm × 95 cm )

Definizione (Rettangolo Tatami)

Si definisce Rettangolo Tatami un rettangolo in

cui una dimensione è pari al doppio dell’altra.

Esempio di Rettangolo Tatami: rettangolo

avente misura di base 6 cm e di altezza 3 cm.

Tatami Room Patterns

I pavimenti realizzati con il rettangolo tatami

hanno delle configurazioni standard. Si riportano

nella successiva immagine i patterns più diffusi.

Prova a inventare degli esercizi che riguardano il

Tatami anche basandoti sulle composizioni presenti

nell’immagine seguente.


20

06.06 – Il Rombo

06.06.a) Definizione (Rombo)

Si definisce Rombo o Losanga un quadrilatero avente tutti i lati congruenti.

06.06.b) Teorema

Tutti i rombi sono parallelogrammi.

Cosa si conclude dunque? Che anche

l’insieme dei rombi similmente a quello

dei rettangoli, ma distintamente da esso è

un sottoinsieme dell’insieme dei

parallelogrammi.

Poiché ogni rombo è un parallelogramma, valgono per i rombi tutte le proprietà che valgono per i

parallelogrammi a cui si aggiungono quelle enunciate nei prossimi paragrafi.

06.06.c) Primo Teorema sulle Diagonali del Rombo

Se un quadrilatero è un rombo allora ha le diagonali perpendicolari.

06.06.d) Secondo Teorema sulle Diagonali del Rombo

Se un quadrilatero è un rombo allora le diagonali dividono in due angoli uguali gli angoli interni

del rombo.


21

06.06.e) Calcolo dell’Area di un Rombo

Dato un rombo, si consideri:

la lunghezza d1 della sua prima diagonale.

la lunghezza d2 della sua seconda diagonale.

L’area del rombo vale: [(Lunghezza Prima Diagonale)] (Lunghezza Seconda Diagonale)

Romb =

o2

Area

Cioè, in linguaggio simbolico: Rombo =2

d dArea

1 2

Corretto utilizzo dei termini diagonale maggiore e diagonale minore

- Nella scuola primaria e talvolta anche nella secondaria di primo grado, tali nomenclature sono

sconsigliabili dal punto di vista didattico a causa del conflitto cognitivo che sopravviene quando

si osserva che i quadrati sono anche rombi. Lo studente (e non solo), in tali casi, incontra

difficoltà perché riconosce una coppia di segmenti aventi la stessa lunghezza e non una

―diagonale maggiore‖ e una ―diagonale minore‖. Per includere tali casi particolari - mantenendo

tali tradizionali nomi a cui tutti sono ―affezionati‖ - dovremmo denominarle, più rigorosamente,

―diagonale maggiore o uguale‖ e ―diagonale minore o uguale‖.

- Nella secondaria di secondo grado, invece, è bene utilizzare anche i termini diagonale maggiore

e diagonale minore, in quanto, è una bella occasione per affrontare il discorso dei ―casi limite‖.

Osservazione

Nei rombi — che sono trapezi particolari — tutti i lati sono sia basi sia lateral sides.

06.07 – Il Quadrato

06.07.a) Definizione (Quadrato)

Si definisce Quadrato un quadrilatero avente tutti gli angoli e i lati congruenti.

06.07.b) Teorema

Tutti i quadrati sono aquiloni.

06.07.c) Teorema

Tutti i quadrati sono parallelogrammi.


22

06.07.d) Teorema

Tutti i quadrati sono rettangoli.

06.07.e) Teorema

Tutti i quadrati sono rombi.

Osservazione

L’insieme dei quadrati (come quelli dei rettangoli e dei rombi) è un sottoinsieme dell’insieme dei

parallelogrammi e quindi valgono per i quadrati tutte le proprietà che valgono per i

parallelogrammi.

Ogni quadrato è sia un rombo (poiché ha i quattro lati congruenti), sia un rettangolo (poiché ha i

quattro angoli congruenti). Viceversa se un rettangolo (che ha quattro angoli congruenti) è anche

un rombo, allora ha anche quattro lati congruenti e quindi è necessariamente un quadrato. Dal

punto di vista della Teoria degli Insiemi, dunque, l’insieme dei quadrati, rappresenta l’intersezione

degli insiemi dei rettangoli e dei rombi.

Per i quadrati, inoltre, valgono quindi sia le proprietà dei rettangoli che quelle dei rombi. In

particolare si ha che:

le diagonali di un quadrato sono congruenti (in quanto il quadrato è un rettangolo);

le diagonali di un quadrato sono perpendicolari (in quanto il quadrato è un rombo);

Osservazione

Nei quadrati, come visto per il parallelogramma, il rettangolo e il rombo — che sono trapezi

particolari — tutti i lati sono al contempo sia basi che lateral sides.

06.07.f) Calcolo dell’Area di un Quadrato

Dato un quadrato, si consideri:

la lunghezza l dei suoi lati.

L’area del quadrato vale: 2Quadrato (Lunghezza Lato del Quadrato)=Area

Cioè, in linguaggio simbolico: 2Quadrato = lArea


23

06.08 – Quadrilateri Simili

06.08.a) Definizione di Quadrilateri Simili

Due quadrilateri si dicono Quadrilateri Simili se:

- hanno tutti gli angoli rispettivamente congruenti;

- le lunghezze dei lati corrispondenti sono proporzionali secondo un rapporto costante pari a k

(Rapporto di Similitudine).

06.08.b) Teorema (Perimetro di Figure Simili)

Il rapporto dei perimetri di figure simili è pari al rapporto di similitudine k.

06.08.c) Teorema (Area di Figure Simili)

Il rapporto delle misure delle aree di figure simili è pari a k2 e cioè al quadrato del rapporto di

similitudine.

06.08.d) Misconcezione Frequente sulla Definizione di Similitudine

Spesso gli studenti - e non solo – riportano la seguente definizione errata (in quanto incompleta):

―Due figure geometriche si dicono Figure Simili se hanno tutti gli angoli corrispondenti

congruenti‖.

Questo errore è dovuto alla ―naturale‖ tentazione di estendere il I Criterio di Similitudine dei

Triangoli ([§05.13.g]: Due triangoli sono simili se hanno due angoli rispettivamente congruenti) ai

poligoni con più di tre lati. Ciò purtroppo non si verifica, dimostriamolo con un controesempio.

Controesempio

Si considerino un qualunque quadrato avente lato di misura l = 4 cm e un rettangolo avente

dimensioni di misura b = 6 cm e h = 4 cm. Le due figure così ottenute, pur avendo tutti gli angoli

congruenti, sono evidentemente figure non simili! La seconda parte della definizione (―…e i lati

corrispondenti con misure di lunghezza in rapporto costante pari a k‖), dunque, è fondamentale!


24

06.09 – Quadrilateri Isoperimetrici

06.09.a) Definizione (Figure Isoperimetriche)

Due figure geometriche A e B si dicono Figure Isoperimetriche se hanno lo stesso perimetro.

06.09.b) Definizione (Quadrilateri Isoperimetrici)

Due quadrilateri A e B si dicono Quadrilateri Isoperimetrici se hanno lo stesso perimetro.

06.09.c) Osservazione

Due figure geometriche A e B se sono isoperimetriche non necessariamente sono congruenti.

Controesempio

Si considerino un qualunque quadrato avente lato di misura l = 5 cm e un rettangolo avente

dimensioni di misura b = 6 cm e h = 4 cm. Le due figure così ottenute, pur avendo lo stesso

perimetro (20 cm), evidentemente sono figure non congruenti!

06.10 – Quadrilateri Equiestesi

06.10.a) Definizione (Superfici Equiestese/Equivalenti)

Due superfici A e B si dicono Superfici Equiestese o Superfici Equivalenti se hanno la stessa

area.

Notazione

Date due generiche figure geometriche A e B, per indicare che A equiestesa B si scriverà:

A B

06.10.b) Definizione (Quadrilateri Equiestesi/Equivalenti)

Due quadrilateri si dicono Quadrilateri Equiestesi o Quadrilateri Equivalenti se e soltanto se

hanno la stessa area.


25

06.10.c) Osservazione

Due figure geometriche A e B se sono equiestese non necessariamente sono congruenti.

Controesempio

Si considerino un qualunque quadrato

avente lato di misura l = 6 cm e un

rettangolo avente dimensioni di misura:

b = 9 cm e h = 4 cm.

Le due figure così ottenute, pur avendo

aree della stessa misura (36 cm2),

evidentemente sono figure non congruenti!


26

SINTESI DELLE DEFINIZIONI DEL “MONDO QUADRILATERO”

Definizione (Quadrilatero Scaleno).

Si definisce Quadrilatero Scaleno un quadrilatero che non ha né angoli e né lati congruenti.

Definizione (Trapezio)

Si definisce Trapezio un quadrilatero che ha (almeno) una coppia di lati paralleli.

Dato un trapezio, si definiscono:

– Basi del Trapezio i lati paralleli del trapezio;

– Lateral Sides, gli altri due lati non considerati come basi (su altri testi anche denominati Lati

Obliqui).

Definizione (Trapezio Rettangolo)

Si definisce Trapezio Rettangolo un trapezio con almeno due lati perpendicolari.

Definizione (Trapezio Isoscele)

Si definisce Trapezio Isoscele un quadrilatero con almeno due lati paralleli e gli angoli adiacenti a uno

di essi congruenti.

Definizione (Trapezio Scaleno)

Si definisce Trapezio Scaleno un trapezio non isoscele.

Definizione (Parallelogramma)

Si definisce Parallelogramma un quadrilatero avente i lati opposti paralleli.

Definizione (Aquilone)

Si definisce Aquilone o Deltoide o Kite un quadrilatero in cui ci sono due lati consecutivi congruenti e

gli altri due sono a loro volta tra loro congruenti.

Definizione (Romboide)

Si definisce Romboide un parallelogramma che non ha né lati consecutivi congruenti né angoli

adiacenti congruenti.

Definizione (Rettangolo)

Si definisce Rettangolo un quadrilatero avente tutti gli angoli congruenti.

Definizione (Rombo o Losanga)

Si definisce Rombo o Losanga un quadrilatero avente tutti i lati congruenti.

Definizione (Quadrato)

Si definisce Quadrato un quadrilatero avente tutti gli angoli e i lati congruenti.

Bibliografia

Tortorelli L. (edizione marzo 2017). Geometriko, Trento: Edizioni Erickson.

D’Amore B. (1999). Elementi di didattica della matematica. Bologna: Pitagora.

D’Amore B. (2003). Le basi filosofiche, pedagogiche, epistemologiche e concettuali della Didattica

della Matematica. Bologna: Pitagora.

D’Amore B., Sbaragli S. (2005). Analisi semantica e didattica dell’idea di ―misconcezione‖. La

matematica e la sua didattica. 2, 139-163.

Radford L. (2005) La generalizzazione matematica come processo semiotico. La matematica e la sua

didattica. 2, 191-213.

Sbaragli S. (2005). Misconcezioni ―inevitabili‖ e misconcezioni ―evitabili‖. La matematica e la sua

didattica. 1, 57-71.

Duval R. (2006). Trasformazioni di rappresentazioni semiotiche e prassi di pensiero in matematica. La

matematica e la sua didattica. 4, 585-619.

Baddeley A. e Hitch G. (1974), Working memory. In G.H. Bower (a cura di), The psychology of

learning and motivation: Advances in research and theory, vol. 8, pp. 47-89, New York, NY,

Academic Press.

Clements D.H. e Sarama J. (2000), Young children’s ideas about geometric shapes, «Teaching

Children Mathematics», vol. 6, pp. 482-488.

Crowley M.L. (1987), The Van Hiele model of the development of geometric thought. In M.M.

Lindquist (a cura di), Learning and teaching geometry, K-12, Reston, VA, National Council of

Teachers of Mathematics, pp. 1-16.

Kosslyn S.M. (1980), Image and Mind, Cambridge, MA, Harvard University Press.

Linn M.C. e Peterson A.C. (1985), Emergence and characterization of sex differences in spatial

ability: A meta-analysis, «Child Development», vol. 56, n. 6, pp. 1479-1498.

Lucangeli D. (2009), Conosco le forme: Valutare e potenziare l’apprendimento della geometria dai 4

ai 6 anni, Firenze, Giunti Scuola.

Maier H. (1993), Problemi di lingua e di comunicazione durante le lezioni di matematica, «La

Matematica e la sua Didattica», vol. 1, pp. 69-80.

Mammarella I.C., Pazzaglia F. e Cornoldi C. (2008), Evidence for different components in children’s

visuospatial working memory, «British Journal of Developmental Psychology », vol. 26, pp. 337-355.

Pazzaglia F. e Cornoldi C. (1999), The role of distinct components of visuo-spatial working memory in

the processing of texts, «Memory», vol. 7, pp. 19-41.

Piaget J. e Inhelder B. (1948), La représentation de l’espace chez l’enfant, Parigi, Presses

Universitaires de France.

Unione Matematica Italiana (2003), Matematica 2003: La matematica per il cittadino,

www.dm.unibo.it.

van Hiele P.M. (1984), A child’s thought and geometry. In D. Fuys, D. Geddes e R. Tishler, English

translation of selected writings of Dina van Hiele Geldof and Pierre M. van Hiele, Brooklin, NY, pp.

243-252.

van Hiele P.M. (1986), Structure and insight: A theory of mathematics education, Orlando, FL,

Academic Press.

Vygotskij L. (1974), Storia dello sviluppo delle funzioni psichiche superiori e altri scritti, Firenze,

Giunti-Barbera.

Volume VI - Diretto€¦ · lunghezza pari a 5 cm: potrebbe essere un rombo, ma anche un quadrato....

Documents

Transcript of Volume VI - Diretto€¦ · lunghezza pari a 5 cm: potrebbe essere un rombo, ma anche un quadrato....