UNIVERSITA di ROMA “LA SAPIENZA”` Corso di Laurea in Ingegneria Informatica...

UNIVERSITA di ROMA “LA SAPIENZA”

Corso di Laurea in Ingegneria Informatica

anno accademico 2000–2001

Esercitazioni Laboratorio:

AMPL

A Modeling Language For Mathematical Programming

Canale L–O

Dipartimento di Informatica e Sistemistica

Universita di Roma “La Sapienza”

versione preliminare di dicembre 2000

Esercitazione 1

Modello di Produzione multi-plan

Si consideri il modello di pianificazione della produzione multi-plant dell’Esempio 2.2.4.

Si riporta brevemente la descrizione del problema:

Un’industria manifatturiera possiede due impianti di Produzione e fabbrica due tipi di Prodotti P1 e P2

utilizzando due macchine utensili: una per la levigatura e una per la pulitura. Per avere un Prodotti finito enecessaria l’utilizzazione di entrambe le macchine. Il primo impianto ha una disponibilita massima settimanaledi 80 ore della macchina per la levigatura e di 60 ore della macchina per la pulitura. Le disponibilita orariedelle due macchine nel secondo impianto sono rispettivamente di 60 e 70 ore settimanali. La tabella che segueriporta, per ciascun Prodotti, il numero di ore di lavorazione necessarie su ciascuna macchina per ottenere unProdotti finito (poiche le macchine possedute dal secondo impianto sono piu vecchie, i tempi di utilizzo sonomaggiori)

Impianto 1 Impianto 2

P1 P2 P1 P2

levigatura 4 2 5 3pulitura 2 5 5 6

Inoltre ciascuna unita di Prodotti utilizza 4 Kg di materiale grezzo. Il profitto netto (in migliaia di lire) ottenutodalla vendita di una unita di Prodotti P1 e P2 e rispettivamente di 10 e 15.

(a) Costruire un modello lineare che permetta di massimizzare il profitto complessivo ottenuto dalla venditadei Prodotti in ciascun impianto sapendo che settimanalmente l’industria decide di assegnare 75 Kg dimateriale grezzo al primo impianto e 45 Kg di materiale grezzo al secondo impianto.

(b) Costruire un modello lineare che permetta di massimizzare il profitto complessivo ottenuto dalla venditadei Prodotti supponendo che l’industria non allochi a priori 75 Kg di materiale grezzo nel primo impiantoe di 45 Kg di materiale grezzo nel secondo impianto, ma lasci al modello la decisione di come ripartiretra i due impianti 120 Kg complessivi disponibili di questo materiale grezzo.

Si riportano sinteticamente le formulazioni ottenute.

1

Formulazione del caso (a)Questo caso, nella pratica, corrisponde a costruire due modelli indipendenti: uno riferito al primoimpianto, uno riferito al secondo impianto. Una “risorsa” (il materiale grezzo) e gia allocata a priori.

Impianto 1: La formulazione relativa al primo impianto e:

max(10x1 + 15x2)4x1 + 4x2 ≤ 754x1 + 2x2 ≤ 802x1 + 5x2 ≤ 60x1 ≥ 0, x2 ≥ 0

A questo punto, prima di passare all’impianto 2, vediamo come fare per scrivere in AMPL Plus ilprecedente problema di PL. Per fare questo e sufficiente creare il seguente file di modello (un semplicefile di testo ma con estensione .mod) ad esempio impianto1.mod.

impianto1.mod

var x1;

var x2;

maximize profitto: 10*x1 + 15*x2;

subject to m_grezzo: 4*x1 + 4*x2 <= 75;

subject to levigatura: 4*x1 + 2*x2 <= 80;

s.t. pulitura: 2*x1 + 5*x2 <= 60;

s.t. x1_non_neg: x1 >= 0;


Ora esaminiamo nel dettaglio il file impianto1.mod di sopra. Notiamo che:- ogni variabile e definita da una istruzione var;- la funzione obiettivo viene definita da una istruzione che comincia con la parola chiave maximize

(o minimize nel caso il problema fosse di minimizzazione) seguita da un nome per la funzioneobiettivo (in questo caso profitto);

- ogni vincolo e definito in una istruzione che comincia con la parola chiave subject to (ma e pos-sibile anche l’abbreviazione s.t.) seguita da un nome simbolico per il vincolo stesso. In questocaso abbiamo usato i nomi m grezzo, levigatura, pulitura, x1 non neg, x2 non neg.

A questo punto, per risolvere il problema in AMPL Plus e sufficiente aprire il file impianto1.mod,quindi, dal menu Run della finestra di AMPL Plus, scegliere prima la voce Build model e poi Solve

2

problem. Se il solutore scelto e in grado di risolvere il problema che abbiamo scritto, sara possibilevedere i risultati dell’ottimizzazione scegliendo, sempre dal menu Run, il comando Build results.Se il file di modello e stato scritto correttamente, all’ottimo l’impianto 1 ha un profitto di 225 ottenutofabbricando 11, 25 unita di P1 e 7, 5 di P2. In particolare si e utilizzato tutto il materiale grezzo esono state sfruttate tutte le ore di pulitura a disposizione. Le macchine per la levigatura, invece, sonostate sottoutilizzate essendo avanzate 20 ore di tempo macchina.

Impianto 2: La formulazione relativa al secondo impianto e:

max(10x3 + 15x4)4x3 + 4x4 ≤ 455x3 + 3x4 ≤ 605x3 + 6x4 ≤ 75x3 ≥ 0, x4 ≥ 0

Il modello in AMPL Plus per l’impianto 2 e:

impianto2.mod

var x3;

var x4;

maximize profitto: 10*x3 + 15*x4;

subject to m_grezzo: 4*x3 + 4*x4 <= 45;

subject to levigatura: 5*x3 + 3*x4 <= 60;

s.t. pulitura: 5*x3 + 6*x4 <= 75;



all’ottimo l’impianto 2 ha un profitto di 168, 75 ottenuto fabbricando 11, 25 unita di P2 e nessunaunita di P1. In particolare e stato utilizzato tutto il materiale grezzo ma, sia le macchine per lalevigatura che quelle per la pulitura, sono state sottoutilizzate essendo avanzate rispettivamente 26, 25e 7, 5 ore di tempo macchina.

3

Formulazione del caso (b)Questo caso corrisponde a costruire un unico modello comprendente entrambi gli impianti. L’allocazionedella “risorsa” data dal materiale grezzo e lasciata al modello stesso.

La formulazione relativa a questo caso e:

max (10x1 + 15x2 + 10x3 + 15x4)4x1 + 4x2 + 4x3 + 4x4 ≤ 1204x1 + 2x2 ≤ 802x1 + 5x2 ≤ 60

5x3 + 3x4 ≤ 605x3 + 6x4 ≤ 75

x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0

in AMPL si avra:

impianto1e2.mod

var x1;

var x2;

var x3;

var x4;

maximize profitto: 10*(x1+x3) + 15*(x2+x4);

s.t. m_grezzoTOT: 4*(x1+x2+x3+x4) <= 120;

s.t. levigatura1: 4*x1 + 2*x2 <= 80;

s.t. pulitura1: 2*x1 + 5*x2 <= 60;

s.t. levigatura2: 5*x3 + 3*x4 <= 60;

s.t. pulitura2: 5*x3 + 6*x4 <= 75;





Facendo risolvere il precedente modello ad AMPL otteniamo un profitto complessivo di 404, 17 ottenutofabbricando nell’impianto 1: 9, 17 unita di P1 e 8, 33 unita di P2 e fabbricando, nell’impianto 2, solo12, 5 unita di P2. E importante notare i seguenti punti:

4

- il profitto totale in questo caso (404, 17) e superiore alla somma dei profitti ottenuti considerandoseparatamente i due modelli;

- l’impianto 1 ora usa 70Kg di materiale grezzo (contro i 75Kg di prima) mentre l’impianto 2 neusa 50Kg (contro i 45Kg di prima).

AMPL consente di scrivere il problema in modo diverso, separando il modello dai dati. Il modellorelativo all’impianto 1 puo essere infatti riscritto come:

impianto.mod

set Prodotti;

set Risorse;

param q_max{Risorse} >=0;

param richiesta{Risorse,Prodotti} >=0;

param prezzo{Prodotti} >=0;

var x{Prodotti} >=0;

maximize profitto: sum{i in Prodotti} prezzo[i]*x[i];

s.t. vincolo_risorsa {j in Risorse}:

sum{i in Prodotti} richiesta[j,i]*x[i] <= q_max[j];

Ora analiziamo le istruzione del file impianto.mod. Anzitutto notiamo le istruzioni

set Prodotti;

set Risorse;

con le quali si dichiarano Prodotti e Risorse come insiemi di un numero imprecisato di elementi(prodotti e risorse). Subito dopo abbiamo tre istruzioni che ci servono per definire altrettanti parametridel modello. La prima di queste

param q_max{Risorse}>=0;

5

definisce un vettore di parametri con tante componenti quanti sono gli elementi dell’insieme Risorse

e definisce le quantita massime disponibili di ciascuna risorsa.Il >= 0 specifica che i valori immessi devono essere non negativi, AMPL eseguira automaticamente ilcontrollo sui dati.L’istruzione successiva ovvero

param richiesta{Risorse,Prodotti}>=0;

definisce invece una matrice di parametri con tante righe quanti sono le risorse e tante colonne quantesono i prodotti, specificando per ogni prodotto la quantita di risorsa necessaria alla sua realizzazione.L’ istruzione

param prezzo{Prodotti} >=0;

definisce un vettore di parametri con tante componenti quanti sono gli elementi dell’insieme Prodottispecificando il prezzo di ogni prodotto.La funzione obiettivo profitto e definita dalla istruzione

maximize profitto: sum{i in Prodotti} prezzo[i]*x[i];

Infine e interessante notare l’ultima istruzione

s.t. vincolo_risorsa {j in Risorse}:

sum{i in Prodotti} richiesta[j,i]*x[i] <= q_max[j];

con la quale si definiscono tanti vincoli quanti sono gli elementi dell’insieme Risorse.Bisogna poi definire un file con estensione .dat dove vengono specificati i valori per gli insiemi e iparametri del modello. Per quanto riguarda l’impianto 1 si avra:

impianto1.dat

set Prodotti := P1 P2;

set Risorse := m_grezzo levigatura pulitura;

param: q_max :=

6

m_grezzo 75

levigatura 80

pulitura 60;

param richiesta: P1 P2 :=

m_grezzo 4 4

levigatura 4 2

pulitura 2 5;

param: prezzo :=

P1 10

P2 15;

Facciamo notare che in questo modo, avendo cioe a disposizione il file impianto.mod contenente ilmodello separato dai dati del problema (contenuti invece nel file impianto1.dat), possiamo risolveredifferenti problemi di massimizzazione del profitto semplicemente cambiando i dati contenuti nel filecon estensione .dat.Sfruttando questo fatto e banalissimo risolvere in AMPL il problema relativo all’impianto 2 utilizzandolo stesso file .mod e un diverso file .dat, che e il seguente:

impianto2.dat

set Prodotti := P1 P2;

set Risorse := m_grezzo levigatura pulitura;

param: q_max :=

m_grezzo 45

levigatura 60

pulitura 75;

param richiesta: P1 P2 :=

m_grezzo 4 4

levigatura 5 3

pulitura 5 6;

7

param: prezzo :=

P1 10

P2 15;

Nello stesso modo, cioe specificando il solo file dei dati, e possibile risolvere il problema completo:

impianto.dat

set Prodotti := P1_impianto1 P2_impianto1 P1_impianto2 P2_impianto2;

set Risorse := m_grezzo levigatura1 pulitura1 levigatura2 pulitura2;

param: q_max :=

m_grezzo 120

levigatura1 80

pulitura1 60

levigatura2 60

pulitura2 75;

param richiesta: P1_impianto1 P2_impianto1 P1_impianto2 P2_impianto2:=

m_grezzo 4 4 4 4

levigatura1 4 2 0 0

pulitura1 2 5 0 0

levigatura2 0 0 5 3

pulitura2 0 0 5 6;

param: prezzo :=

P1_impianto1 10

P2_impianto1 15

P1_impianto2 10

P2_impianto2 15;

8

Esercitazione 2

Modello di “lot sizing”

Si consideri il modello di “lot sizing” dell’Esempio 2.2.10.

Si riporta brevemente una descrizione del problema:

Un’industria deve pianificare la produzione di un unico prodotto per i prossimi tre mesi. La domanda mensile

che il mercato e in grado di assorbire e nel primo, nel secondo e nel terzo mese pari rispettivamente a 120,

150 e 90 tonnellate. Questa industria dispone di magazzini e quindi ha la possibilita di stockare, le quantita

prodotte nel primo o nel secondo mese, ma al termine del trimestre non intende lasciare scorte in magazzino.

Lo stockaggio ha un costo unitario (in migliaia di Euro per tonnellata) pari a 2. Infine per la produzione di

ciascuna tonnellata di prodotto l’industria deve sostenere un costo (variabile nei tre mesi) pari a 10, 12 e 11

migliaia di Euro rispettivamente nel primo, nel secondo e nel terzo mese. Si deve determinare quanto produrre

mensilmente e quanto stockare nei primi due mesi in modo da minizzare il costo complessivo.

E un problema di “lot sizing” che puo essere formulato come segue.

min (10x1 + 12x2 + 11x3 + 2s1 + 2s2)x1 = 120 + s1

x2 + s1 = 150 + s2

x3 + s2 = 90x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, s1 ≥ 0, s2 ≥ 0.

Prima di procedere nella scrittura nel linguaggio di AMPL di questo problema di ProgrammazioneLineare si ricorda che tutte le istruzioni nel linguaggio AMPL devono terminare con “ ; ”ed il numero di spazi bianchi inseriti e del tutto arbitrario.

Segue un file .mod contenente il modello scritto nel linguaggio di AMPL.

9

lotsizing1.mod

#### SEZIONE PER LA DICHIARAZIONE DELLE VARIABILI ####

var x1 ; # dichiarazione variabile reale x1



var s1 ; # dichiarazione variabile reale s1

var s2 ; # dichiarazione variabile reale s2

#### SEZIONE PER LA DICHIARAZIONE DELLA FUNZIONE ####

#### OBIETTIVO E DEI VINCOLI ####

minimize cost: 10*x1 + 12*x2 + 11*x3 + 2*s1 + 2*s2;

# la funzione obiettivo

s.t. equil_mese1: x1 = 120 + s1; # s.t.= subject to...

s.t. equil_mese2: x2 + s1 = 150 + s2; # sono necessari i ":"

s.t. equil_mese3: x3 + s2 = 90; # dopo le label

s.t. vincx1: x1 >= 0; # vincolo di non negativita’ per x1



s.t. vincs1: s1 >= 0; # vincolo di non negativita’ per s1

s.t. vincs2: s2 >= 0; # vincolo di non negativita’ per s2

Osservare la presenza di due sezioni: la sezione per la dichiarazione delle variabili e la sezione perla dichiarazione della funzione obiettivo e dei vincoli. La funzione obiettivo e riconoscibile mediantele parole chiave minimize o maximize. Il nome cost e solo una “label” (etichetta) e puo esseremodificata a piacimento. Dopo le label (sia nella funzione obiettivo sia nei vincoli sono necessari i “ :”). I caratteri inseriti dopo il simbolo “ # ” fino al termine della linea non sono considerati da AMPL,quindi tale simbolo puo essere utilizzato per inserire frasi di commento.

E inoltre possibile integrare nella dichiarazione delle variabili i vincoli di non negativita delle variabilie quindi possiamo riscrivere il modello nella seguente forma:

10

lotsizing2.mod


var x1 >= 0 ; # i vincoli di non negativita’ delle variabili

var x2 >= 0 ; # sono stati integrati nella dichiarazione

var x3 >= 0 ; # stessa delle variabili

var s1 >= 0 ;

var s2 >= 0 ;



minimize cost: 10*x1 + 12*x2 + 11*x3 + 2*s1 + 2*s2;

s.t. equil_mese1: x1 - s1 = 120; # le variabili possono

s.t. equil_mese2: x2 + s1 - s2 = 150; # essere ordinate

s.t. equil_mese3: x3 + s2 = 90; # rispetto ad un

# criterio qualsiasi

E inoltre possibile parametrizzare il modello dichiarando i parametri prima del loro uso del modello.Questo permette di costruire un modello che non contiene esplicitamente i dati del problema chevengono assegnati a dei parametri e in questo modo si separano i dati dal modello permettendol’utilizzo del modello scritto in forma parametrizzata anche in presenza di nuovi dati. Il modello giaconsiderato puo essere quindi riscritto nella seguente forma:

lotsizing3.mod

#### SEZIONE PER LA DICHIARAZIONE DEI PARAMETRI ####

param cost_produz1 ; # e’ possibile parametrizzare il problema

param cost_produz2 ; # dichiarando i parametri prima del loro

param cost_produz3 ; # uso nel modello

param cost_scorta1 ;

param cost_scorta2 ;

11

param domanda1 ;

param domanda2 ;

param domanda3 ;


var x1 >= 0 ;

var x2 >= 0 ;

var x3 >= 0 ;

var s1 >= 0 ;

var s2 >= 0 ;



minimize cost:

cost_produz1*x1 + cost_produz2*x2 + cost_produz3*x3 +

cost_scorta1*s1 + cost_scorta2*s2;

s.t. equil_mese1: x1 - s1 = domanda1;

s.t. equil_mese2: x2 + s1 - s2 = domanda2;

s.t. equil_mese3: x3 + s2 = domanda3;

Quando si utilizza una scrittura parametrizzata del modello e necessario introdurre i dati del problemamediante la loro scrittura in un file con estensione .dat. Per introdurre i dati nel modello precedentesi puo quindi scrivere il seguente file

lotsizing3.dat

param cost_produz1 := 10;



param cost_scorta1 := 2;

param cost_scorta2 := 2;

param domanda1 := 120;



12

E possibile inoltre inserire un controllo sulla non negativita dei parametri introdotti riscrivendo lasezione per la dichiarazione dei parametri nella forma

lotsizing3b.mod


param cost_produz1 >=0;



param cost_scorta1 >=0;

param cost_scorta2 >=0;

param domanda1 ;

param domanda2 ;

param domanda3 ;

E inoltre possibile parametrizzare il modello introducendo vettori di parametri. In questo caso l’insiemeche indicizza il vettore si introduce con l’istruzione set. In questo modo e anche possibile dichiararevettori di variabili. Si aggiunge quindi una sezione per la dichiarazione degli insiemi e il modello puoessere riscritto nella forma

lotsizing4.mod

#### SEZIONE PER LA DICHIARAZIONE DEGLI INSIEMI ####

set PERIODI;

set SCORTE;


param cost_produz {PERIODI} >= 0; # e’ possibile parametrizzare il

# problema introducendo vettori

# di parametri

param cost_scorte {SCORTE} >= 0;

param domanda {PERIODI} >= 0;

param A{PERIODI,PERIODI} >= 0;

param B{PERIODI,SCORTE} ;

13


var x {i in PERIODI} >= 0 ; # e’ possibile dichiarare vettori

# di variabili

var s {j in SCORTE} >= 0 ;



minimize cost: sum{i in PERIODI} cost_produz[i]*x[i] +

sum{j in SCORTE} cost_scorte[j]*s[j];

s.t. equil_mese {i in PERIODI}: sum{j in PERIODI} A[i,j]*x[j] +

sum{k in SCORTE} B[i,k]*s[k] = domanda[i]

# i vincoli precedenti possono essere

# alternativamente introdotti mediante

# le seguenti relazioni

# s.t. equil_mese1: x1 - s1 = domanda1;

# s.t. equil_mese2: x2 + s1 - s2 = domanda2;

# s.t. equil_mese3: x3 + s2 = domanda3;

In questo caso il file di dati dovranno essere specificati i valori per insiemi e per i parametri. Il file didati per il modello in esame e il seguente

lotsizing4.dat

set PERIODI := PER1 PER2 PER3;

set SCORTE := MAG_1-2 MAG_2-3;

param: cost_produz domanda :=

PER1 10 120

PER2 12 150

PER3 11 90 ;

param: cost_scorte :=

14

MAG_1-2 2

MAG_2-3 2 ;

param A: PER1 PER2 PER3 :=

PER1 1 0 0

PER2 0 1 0

PER3 0 0 1 ;

param B: MAG_1-2 MAG_2-3 :=

PER1 -1 0

PER2 +1 -1

PER3 0 +1 ;

ESERCIZIOConsideriamo un esempio di problema di allocazione ottima di risorse gia esaminato del quale si riportabrevemente una descrizione:

Un colorificio produce due tipi di coloranti C1 e C2 utilizzando 3 preparati base in polvere P1, P2, P3 chevengono sciolti in acqua. La differente concentrazione dei preparati base da origine ai due diversi tipi di coloranti.Le quantita (in ettogrammi) di preparati base necessarie per produrre un litro di colorante di ciascuno dei duetipi e riportato nella seguente tabella

C1 C2

P1 1 1P2 1 2P3 - 1

Ogni giorno la quantita di ciascuno dei preparati base (in ettogrammi) della quale il colorificio puo disporre ela seguente

P1 P2 P3

750 1000 400

Il prezzo di vendita del colorante C1 e di 7000 lire al litro, mentre il colorante C2 viene venduto a 10000 lire

al litro. Determinare la strategia ottimale di produzione giornaliera in modo da massimizzare i ricavi ottenuti

dalla vendita dei due coloranti.

Come gia visto, una formulazione di Programmazione Lineare per questo problema e la seguente:

max (7x1 + 10x2)x1 + x2 ≤ 750x1 + 2x2 ≤ 1000x2 ≤ 400x1 ≥ 0, x2 ≥ 0.

15

Si riportano di seguito i file .mod e .dat del modello in esame:

coloranti.mod

set Coloranti;

set Preparati;

param profitti{Coloranti}>=0;

param q_max{Preparati}>=0;

param rich{Preparati,Coloranti}>=0;

var x{Coloranti}>=0;

maximize profitto: sum{i in Coloranti} profitti[i]*x[i];

s.t. v_preparati {j in Preparati}: sum{i in Coloranti} rich[j,i]*x[i] <= q_max[j];

coloranti.dat

set Coloranti := c1 c2;

set Preparati := p1 p2 p3;

param:

profitti :=

c1 7000

c2 10000 ;

param:

q_max :=

p1 750

p2 1000

p3 400 ;

param rich :

c1 c2 :=

p1 1 1

p2 1 2

p3 0 1;

16

Esercitazione 3

Modelli di trasporto

Si vogliono considerare un modello di trasporti e alcune sue variazioni da implementare nel linguaggioAMPL. Per dettagli sulla construzione di modelli di questo tipo si rimanda al paragrafo 2.2.3 delle“Lezioni di Ricerca Operativa”.Si descrive brevemente il problema di trasporto che verra preso in esame.

Si devono pianificare i trasporti di un tipo di merce da cinque citta, Asti, Bergamo, Como, Domodossola, Empoli(citta origini) ad altre quattro citta, Mantova, Napoli, Olbia, Palermo (citta destinazioni). La tabella che segueriporta il costo unitario del traporto della merce da ciascuna citta origine a ciascuna citta destinazione, insiemealla domanda di merce da soddisfare esattamente di ogni citta destinazione e alla quantita massima di mercedisponibile presso ciascuna citta origine

Mantova Napoli Olbia Palermo disponibilita max

Asti 1 3.5 4 4.5 100Bergamo 0.1 3 4.5 4.8 110Como 0.3 2.8 4.7 4.9 130Domodossola 1 2.2 3.9 4 85Empoli 1.7 2.2 5 5.3 120domanda 30 18 45 56

Come si puo osservare, la somma dei quantitativi di merce disponibili nelle citta origini e maggiore alla somma

delle domande delle citta destinazione e questo perche nelle citta orgini sono disponibili dei depositi dove

immagazzinare la merce. Si devono pianificare i trasporti dalle citta origini alle citta destinazioni in modo da

minizzare il costo totale dei trasporti.

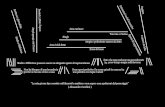
Introdotte le varibili di decisione xij , i = 1, 2, 3, 4, 5, j = 1, 2, 3, 4, associate alla quantita di merce datrasportare dalla citta origine i-esima alla citta destinazione j-esima, indicando con cij il costo unitariodel trasporto dalla citta origine i-esima alla citta destinazione j-esima e indicando rispettivamente conai, i = 1, 2, 3, 4, 5 e bj , j = 1, 2, 3, 4 la disponibilita massima di merce nelle origini e la domanda dimerce nelle destinazioni, un modello lineare che rappresenta il problema in analisi e il seguente:

17

DESTINAZIONI

M

i

2

11

2

3

j

.....

N

c ijc i

ORIGINI

..........

.....

Figura 1: Modello di trasporto

min

5∑

i=1

4∑

j=1

cijxij

4∑

j=1

xij ≤ ai

5∑

i=1

xij = bi

xij ≥ 0

Segue il file trasporto1.mod che realizza un’implementazione in AMPL del modello ora costruito.

trasporto1.mod


set ORIGINI; # introduce l’insieme delle origini

set DESTINAZIONI; # introduce l’insieme delle destinazioni

18


param costo_origdest {ORIGINI,DESTINAZIONI} >= 0;

# e’ un vettore di parametri

# a 2 indici (matrice). Rappresenta

# i costi unitari di trasporto

# (non negativi) dalle origini alle

# destinazioni.

param max_uscita {ORIGINI} >= 0;

# e’ un vettore di parametri ad 1

# indice. Rappresenta la quantita’

# (non negativa) massima di merce

# che puo’ essere trasportata ’DA’

# ciascuna origine.

param domanda {DESTINAZIONI} >=0;



# (non negativa) di merce che deve

# essere trasportata ’VERSO’ ciascuna

# destinazione.


var x {i in ORIGINI,j in DESTINAZIONI} >= 0;

# x[i,j] e’ l’elemento di una matrice di

# variabili (2 indici), rappresenta il

# quantitativo di merce trasportato dalla

# origine ’i’ alla destinazione ’j’.



minimize cost_trasporto: sum{i in ORIGINI,j in DESTINAZIONI}

costo_origdest[i,j]*x[i,j];

# a ciascun trasporto origine/destinazione

# e’ associato un costo, i costi poi vengono

# sommati

s.t. origini {i in ORIGINI}:

sum{j in DESTINAZIONI} x[i,j] <= max_uscita[i] ;

# da ciascuna origine non e’ possibile inviare

# piu’ di un determinato quantitativo di merce.

19

s.t. destinazioni {j in DESTINAZIONI}:

sum{i in ORIGINI} x[i,j] = domanda[j] ;

# a ciascuna destinazione deve arrivare

# esattamente una quantita’ determinata di merce.

Il file trasporto1.dat che permette di specificare i dati da introdurre nel modello precedente e ilseguente

trasporto1.dat

set ORIGINI := asti bergamo como domodossola empoli;

# l’insieme ORIGINI ha 5 elementi

set DESTINAZIONI := mantova napoli olbia palermo;

# l’insieme DESTINAZIONI ha 4 elementi

param: max_uscita :=

asti 100

bergamo 110

como 130

domodossola 85

empoli 120 ;

# il vettore di parametri ’costo_origine’

# ha 5 elementi (tanti quante le origini).

param domanda :=

mantova 30

napoli 18

olbia 45

palermo 56 ;

# il vettore di parametri ’domanda’

# ha 4 elementi (tanti quante le destina-

# zioni). Si noti che quando si assegnano

# gli elementi di un solo vettore non sono

# necessari i ’:’ dopo la parola chiave

# ’param’

20

#### LE SEGUENTI DUE ASSEGNAZIONI SONO EQUIVALENTI ####

#param costo_origdest (tr): asti bergamo como domodossola empoli :=

# mantova 1 .1 .3 1 1.7

# napoli 3.5 3 2.8 2.2 2.2

# olbia 4 4.5 4.7 3.9 5

# palermo 4.5 4.8 4.9 4.0 5.3 ;

param costo_origdest : mantova napoli olbia palermo :=

asti 1 3.5 4 4.5

bergamo .1 3 4.5 4.8

como .3 2.8 4.7 4.9

domodossola 1 2.2 3.9 4.0

empoli 1.7 2.2 5.0 5.3 ;

# la matrice di parametri ’costo_origdest’ contiene

# 4*5 = 20 elementi, uno per ogni coppia origine/de-

# stinazione; non e’ necessario specificare

# lo ’0’ (zero) davanti alla virgola.

EsercizioSupponiamo che nelle origini ci sia un costo di prelevamento della merce di cui tenere conto nel calcolodel costo totale, aggiuntivo al costo dei trasporti. Nella tabella che segue si riporta i costi unitari diprelevamento da ciascuna citta origine.

Asti Bergamo Como Domodossola Empoli

costo prelevamento 2 3 4 7 6

Modificare il file .mod e il file .dat in modo da tener conto di questi costi aggiuntivi.

Chiamati ci, i = 1, 2, 3, 4, 5, i costi unitari di prelevamento nella i-esima citta origine, la funzioneobiettivo che rappresenta il costo complessivo diventa

5∑

i=1

4∑

j=1

cijxij +5

∑

i=1

ci

4∑

j=1

xij

Il file trasporto1es.mod che segue riporta il file del modello modificato in accordo con quanto richiestodall’esercizio

21

trasporto1es.mod










# destinazioni.

param costo_origine {ORIGINI} >= 0;


# ad 1 indice. Rappresenta

# i costi unitari di prelevamento

# (non negativi) da ciascuna delle

# origini.




# (non negativa) massima di merce

# che puo’ essere trasportata ’DA’

# ciascuna origine.




# (non negativa )di merce che deve

# essere trasportata ’VERSO’ ciascuna

# destinazione.







22




costo_origdest[i,j]*x[i,j] + sum{i in ORIGINI}

costo_origine[i]* sum{j in DESTINAZIONI} x[i,j];



# sommati







# a ciascuna destinazione deve arrivare

# una determinata quantita’ di merce.

Come si puo vedere e stato aggiunta l’istruzione

param costo_origine {ORIGINI}

per rappresentare i costi di prelevemento da ciascuna citta origine. Inoltre e stata modificata lafunzione obiettivo.

Il file trasporto1es.dat che segue riporta il nuovo file di dati per il modello modificato come richiestodall’esercizio.

trasporto1es.dat





param: costo_origine max_uscita :=

23

asti 2 100

bergamo 3 110

como 4 130

domodossola 7 85

empoli 6 120 ;

# i vettori di parametri ’costo_origine’

# e ’max_uscita’ hanno 5 elementi (tanti

# quante le origini), pertanto si possono

# fare le assegnazioni contemporaneamente!

param domanda :=

mantova 30

napoli 18

olbia 45

palermo 56 ;






# ’param’


#param costo_orig/dest (tr): asti bergamo como domodossola empoli :=

# mantova 1 .1 .3 1 1.7

# napoli 3.5 3 2.8 2.2 2.1

# olbia 4 4.5 4.7 3.9 5

# palermo 4.5 4.8 4.9 4.0 5.3 ;


asti 1 3.5 4 4.5

bergamo .1 3 4.5 4.8

como .3 2.8 4.7 4.9


empoli 1.7 2.2 5.0 5.3 ;



# stinazione. Non e’ necessario specificare


24

Esaminiamo ora un’ulteriore modifica del modello di trasporti introdotto considerando elementi ag-giuntivi che sono di solito presenti nei problemi di trasporto che si presentano nella realta. Supponiamoquindi che ci sia

1. un costo aggiuntivo da imputarsi a tasse portuali ad ogni unita di merce trasportata alla cittadi Olbia pari a 0.1;

2. un vincolo che impone che almeno i 4/5 della merce trasportata provenga da citta origine delnord Italia;

3. un vincolo che impone che almeno i 2/3 della merce trasportata raggiunga citta destinazione delsud Italia e delle isole.

4. un ulteriore costo di trasporto per ogni unita di merce trasportata per qualche coppia di cittaorigine e citta destinazione da imputarsi, ad esempio, a pedaggi autostradali; la tabella che segueriporta per quali coppia di citta esiste questo costo aggiuntivo e a quanto ammonta

Bergamo—Napoli 2 Domodossola—Mantova 0.5 Empoli—Olbia 3.5Bergamo—Olbia 3.5 Domodossola—Palermo 3.8 Empoli—Palermo 3.1

Per tener conto di queste esigenze aggiuntive, sara necessario introdurre nuovi insiemi nel modello inAMPL: l’insieme NORD delle citta del nord, l’insieme SUD delle citta del sud e l’insieme ISOLE dellecitta che si trovano nelle isole. Inoltre si dovra fare uso degli operatori tra insiemi di intersezione eunione che nel linguaggio di AMPL si indicano rispettivamente con

inter union

L’uso di questi operatori e abbastanza semplice e permette di definire gli insiemi intersezione e unione,ad esempio, nel seguente modo:

set ORIGINI; # introduce l’insieme delle citta’ origini

set DESTINAZIONI; # introduce l’insieme delle citta’ destinazioni

set NORD; # introduce l’insieme di alcune citta’ del nord

set SUD; # introduce l’insieme di alcune citta’ del sud

set ISOLE; # introduce l’insieme di alcune citta’ delle

# isole italiane

set ORI_NORD := ORIGINI inter NORD;

# introduce l’insieme intersezione degli

# insiemi ORIGINI e NORD

set DEST_SUDISOLE := DESTINAZIONI inter {SUD union ISOLE};

# introduce l’insieme intersezione

# dell’insieme DESTINAZIONI con l’insieme

# (SUD unione ISOLE)

25

Il file trasporto2.mod che segue riporta il nuovo modello di trasporti che tiene conto delle nuoveesigenze sia nella funzione obiettivo sia per la presenza di nuovi vincoli.

trasporto2.mod


set ORIGINI; # introduce l’insieme delle citta’ origini

set DESTINAZIONI; # introduce l’insieme delle citta’ destinazioni

set NORD; # introduce l’insieme di alcune citta’ del nord

set SUD; # introduce l’insieme di alcune citta’ del sud

set ISOLE; # introduce l’insieme di alcune citta’ delle

# isole italiane








# le due seguenti dichiarazioni sono equivalenti

# nel senso che definiscono l’insieme COPPIE

# formato da coppie di elementi: uno appartenente

# ad ORIGINI e l’altro a DESTINAZIONI

#set COPPIE := {ORIGINI,DESTINAZIONI};

set COPPIE within {ORIGINI,DESTINAZIONI};



# e’ un vettore di parametri a 2 indici (matrice).

# Rappresenta i costi unitari di trasporto

# (non negativi) dalle origini alle destinazioni.


# e’ un vettore di parametri ad 1 indice.

# Rappresenta i costi unitari di prelevamento

# (non negativi) da ciascuna delle origini.

26



# Rappresenta la quantita’ (non negativo) massima di

# merce che puo’ essere trasportata ’DA’

# ciascuna origine.



# Rappresenta la quantita’ (non negativa) massima di

# merce che puo’ essere trasportata

# ’VERSO’ ciascuna destinazione.

param costo_coppie {COPPIE} >=0;

# per gli elementi (coppie di elementi) appartenenti

# all’insieme COPPIE vi e’ un ulteriore costo

# unitario di trasporto (pedaggio autostradale)

param costo_portuale;

# e’ un costo unitario da imputarsi ad ogni unita’

# di prodotto trasportato alla destinazione "olbia"











costo_origine[i]* sum{j in DESTINAZIONI} x[i,j] +

sum{(i,j) in COPPIE} costo_coppie[i,j] * x[i,j] +

sum{(i,"olbia") in {ORIGINI,DESTINAZIONI}} costo_portuale * x[i,"olbia"];



# sommati; agli elementi appartenenti allo

# insieme COPPIE e’ associato un costo in piu’.

27







# a ciascuna destinazione deve arrivare un determinato

# quantitativo di merce.

s.t. origini_nord: sum {i in ORI_NORD,j in DESTINAZIONI} x[i,j] >= 4/5 *

sum {i in ORIGINI,j in DESTINAZIONI} x[i,j] ;

# dalle citta’ di origine del nord vengono effettuati

# almeno i 4/5 dei trasporti totali.

s.t. destinazioni_isole:

sum {i in ORIGINI,j in DESTINAZIONI : j in {SUD union ISOLE}}

x[i,j] >= 2/3 * sum {i in ORIGINI,j in DESTINAZIONI} x[i,j] ;

# verso le citta’ di destinazione del sud e delle

# isole vengono effettuati almeno i 2/3 dei

# trasporti totali.

Il file di dati trasporto2.dat che segue permette di introdurre i dati assegnati nel modello.

trasporto2.dat





set NORD := asti como domodossola empoli mantova;

# l’insieme delle citta’ del nord Italia

set SUD := bari napoli;

# l’insieme delle citta’ del sud Italia

set ISOLE := olbia palermo;

# l’insieme delle citta’ delle isole d’Italia

28


asti 2 100

bergamo 3 110

como 4 130

domodossola 7 85

empoli 6 120 ;

# i vettori di parametri ’costo_origine’

# e ’max_uscita’ hanno 5 elementi (tanti

# quante le origini), pertanto si possono

# fare le assegnazioni contemporaneamente!

param domanda :=

mantova 30

napoli 18

olbia 45

palermo 56 ;






# ’param’


#param costo_orig/dest (tr): asti bergamo como domodossola empoli :=

# mantova 1 .1 .3 1 1.7

# napoli 3.5 3 2.8 2.2 2.1

# olbia 4 4.5 4.7 3.9 5

# palermo 4.5 4.8 4.9 4.0 5.3 ;


asti 1 3.5 6.0 4.5

bergamo .1 3 4.5 4.8

como .3 2.8 4.7 4.9


empoli 1.7 2.2 5.0 5.3 ;



# stinazione. Non e’ necessario specificare


29

param: COPPIE : costo_coppie :=

bergamo napoli 2

bergamo olbia 3.5

domodossola mantova 0.5

domodossola palermo 3.8

empoli olbia 3.5

empoli palermo 3.1 ;

# le possibili coppie origine/destinazione sono

# 5*4 = 20 ma l’insieme COPPIE ne contiene solo

# 6 !!!!

param costo_portuale := 0.1 ;

# per ogni unita’ di merce che ha come destinazione "olbia"

# vi e’ questo costo aggiuntivo;

30

Esercitazione 4

Interpretazione della dualita

Per esaminare come, assegnato un problema di Programmazione Lineare, le informazioni sul corrispon-dente problema duale sono facilmente ottenibili utilizzando AMPL, facciamo riferimento al sempliceesempio di modello di pianificazione della produzione gia visto nel Paragrafo 3.2.1 delle “Lezioni diRicerca Operativa”, che brevemente riassumiamo.

Un’industria produce due tipi di prodotti: un tipo de luxe e un tipo standard. Per avere un prodotto finito diciascuno dei due tipi sono necessari due ingredienti grezzi I1 e I2 e la lavorazione su una macchina. La tabellache segue riporta le quantita in Kg di ciascuno degli ingredienti e le ore di lavorazione sulla macchina necessarieper ottenere un prodotto finito di ciascuno dei due tipi.

de luxe standard

I1 3 2I2 4 1

ore lavoraz. 2 1

Settimanalmente si hanno a disposizione al piu 1200 Kg dell’ingrediente I1 al piu 1000 Kg dell’ingrediente I2mentre la disponibilita massima settimanale di ore lavorative della macchina e pari a 700. Un prodotto de luxe

e venduto a 24 Euro e un prodotto standard e venduto a 14 Euro. Si vuole pianificare la produzione settimanale

in modo da massimizzare il profitto complessivo assumendo che i prodotti siano frazionabili.

Si tratta di un problema di allocazione ottima di risorse limitate che puo essere formulato comeproblema di Programmazione Lineare nel seguente modo:

(P)

max 24x1 + 14x2

3x1 + 2x2 ≤ 12004x1 + x2 ≤ 10002x1 + x2 ≤ 700x1 ≥ 0, x2 ≥ 0

dove le variabili x1 e x2 rappresentano le quantita di prodotti ripettivamente del tipo de luxe e deltipo standard da fabbricare settimanalmente.

Il problema duale del problema ora formulato e

(D)

min 1200u1 + 1000u2 + 700u3

3u1 + 4u2 + 2u3 ≥ 242u1 + u2 + u3 ≥ 14u1 ≥ 0, u2 ≥ 0, u3 ≥ 0.

31

Implementiamo il problema primale nel linguaggio di AMPL. Seguono il file .mod e .dat che rappre-sentano una possibile implementazione di tale problema.

primale1.mod


set PRODOTTI; # introduce l’insieme dei prodotti

set RISORSE; # introduce l’insieme delle risorse


param max_dispo {RISORSE}>=0;

# array di parametri ciascuno dei quali indica

# la disponibilita’ di ciascuna risorsa.

param profitto {PRODOTTI} >=0;

# ciascuna sua componente indica il profitto

# marginale per uno dei prodotti.

param richieste {RISORSE,PRODOTTI}>=0;

# l’elemento (i,j) indica la quantita’ di

# risorsa i-esimo richiesta per produrre

# un’unita’ di prodotto j-esimo.


var x {j in PRODOTTI} >=0;

# la variabile x[j] rappresenta il quantitativo

# di prodotto j-esimo.

#### FUNZIONE OBIETTIVO E VINCOLI ####

maximize profitto_totale: sum {j in PRODOTTI} profitto[j]*x[j];

# rappresenta il profitto totale.

s.t. vincoli {i in RISORSE}:

sum {j in PRODOTTI} richieste[i,j]*x[j] <= max_dispo[i];

# vincoli sul massimo quantitativo disponibile delle

# risorse (ingredienti e di ore lavorative)

32

primale1.dat

set PRODOTTI:= de_luxe standard;

set RISORSE:= I1 I2 ore_lav;

param max_dispo :=

I1 1200

I2 1000

ore_lav 700 ;

param: profitto:=

de_luxe 24

standard 14 ;

param richieste: de_luxe standard :=

I1 3 2

I2 4 1

ore_lav 2 1 ;

Risolviamo ora questo problema e analizziamo il seguente file dei risultati che AMPL produce.

risultati primale

OBJECTIVES:

profitto_totale = 8880

VARIABLES:

x [*] :=

de_luxe 160

standard 360

;

CONSTRAINTS (Dual Values):

vincoli [*] :=

I1 6.4

I2 1.2

ore_lav 0

;

33

Come si puo vedere, insieme al punto di ottimo

x⋆1 = 160, x⋆

2 = 360

e al valore ottimo della funzione obiettivo 8880 vengono riportate altre informazioni riguardanti ilproblema duale associato. In particolare vengono riportati i valori ottimi della variabili duali (associateai vincoli del problema originario). La soluzione ottima del duale risulta quindi

u⋆1 = 6.4, u⋆

2 = 1.2, u⋆3 = 0

Per verificare cio, implementiamo direttamente il problema duale. Seguono il file .mod e .dat cherealizzano una possibile implementazione del problema duale.

duale1.mod


set COLONNE; # introduce l’insieme delle colonne.

set RIGHE; # introduce l’insieme delle righe.


param matr_coeff {RIGHE,COLONNE}>=0;

# dichiara la matrice dei coefficienti per

# il problema duale.

param noti {RIGHE} >=0;

# dichiara il vettore dei termini noti.

param coeff_obiett {COLONNE} >=0;

# dichiara i coefficienti della funzione

# obiettivo.


var u {j in COLONNE} >=0;

# dichiara il vettore delle variabili duali.

#### FUNZIONE OBIETTIVO E VINCOLI ####

minimize funz_obj_duale: sum {j in COLONNE} coeff_obiett[j]*u[j];

# funzione obiettivo del problema duale.

s.t. vincoli {i in RIGHE}: sum {j in COLONNE} matr_coeff[i,j]*u[j] >= noti[i];

# vincoli del problema duale.

34

duale1.dat

set COLONNE:= COL1 COL2 COL3;

set RIGHE:= RIGA1 RIGA2;

param matr_coeff: COL1 COL2 COL3:=

RIGA1 3 4 2

RIGA2 2 1 1 ;

param: noti:=

RIGA1 24

RIGA2 14 ;

param: coeff_obiett:=

COL1 1201

COL2 1000

COL3 700 ;

Risolvendo questo problema si ha il seguente file di risultati

risultati duale

OBJECTIVES:

funz_obj_duale = 8880

VARIABLES:

u [*] :=

COL1 6.4

COL2 1.2

COL3 0

;


vincoli [*] :=

RIGA1 160

RIGA2 360

;

35

Questi risultati confermano che il valore ottimo delle variabili duali e u⋆1 = 6.4, u⋆

2 = 1.2, u⋆3 = 0 e che

il valore ottimo del problema primale e del problema duale coincide ed e pari a 8880. Naturalmente,in modo del tutto simmetrico, nel file dei risultati relativi al problema duale sono anche riportateinformazioni relative al duale del problema duale, cioe al problema primale. Infatti e riportato ilvalore ottimo delle variabili primali che infatti risultano pari a x⋆

1 = 160, x⋆2 = 360.

Quindi nei risultati forniti da AMPL sono riportate importanti informazioni duali di un problemasenza la necessita di formulare il problema duale.Come visto nell’analisi teorica, (si veda il Paragrafo 3.2.1 delle “Lezioni di Ricerca Operativa”)le variabili duali costituiscono i prezzi ombra e determinano il valore marginale delle risorse. Inparticolare i prezzi ombra rappresentano l’effetto dei cambiamenti nel termine noto dei vincoli: adesempio, incrementando di un valore ∆ la disponibilita dell’ingrediente I1 si ottiene un incrementodel profitto pari a 6.4∆ cioe proporzionale a u⋆

1 che e la variabile duale associata al primo vincolo.Verifichiamo cio cambiando il termine noto del vincolo relativo alla disponibilita di ingrediente I1 datoda 3x1 + 2x2 ≤ 1200; in particolare aumentando di una unita il termine noto (∆ = 1), trasformandocioe il vincolo in 3x1+2x2 ≤ 1201 ci si aspetta un incremento del valore ottimo della funzione obiettivopari a 6.4 e quindi un valore pari a 8886.4. Per verificare cio e sufficiente modificare il file primale1.dat(lasciando ovviamente immutato il file primale1.mod), cambiando il valore del parametro max dispo

relativo a I1 e scrivendo quindi

param max_dispo :=

I1 1201

I2 1000

ore_lav 700 ;

Risolvendo di nuovo il problema, si ottengono i risultati di seguito riportati che confermano quanto cisi aspettava.

risultati primale modificato

OBJECTIVES:

profitto_totale = 8886.4

VARIABLES:

x [*] :=

de_luxe 159.8

standard 360.8

;


vincoli [*] :=

I1 6.4

I2 1.2

ore_lav 0

;

36

Per completare l’analisi dell’interpretazione della dualita, si consideri il seguente esercizio.

EsercizioSi consideri il problema di Programmazione Lineare gia esaminato nel Paragrafo 3.2.1 delle “Lezionidi Ricerca Operativa” dato da

max 3x1 + 2x2

x1 + x2 ≤ 42x1 + x2 ≤ 5−x1 + 4x2 ≥ 2x1 ≥ 0, x2 ≥ 0.

Implementare nel linguaggio di AMPL questo problema.

1. Determinare la soluzione ottima e il valore ottimo della funzione obiettivo.

[Risultato: x⋆ = (1, 3), f⋆ = 9]

2. Senza implementare il problema duale ricavare i prezzi ombra associati a ciascuno dei tre vincoli

[Risultato: u⋆ = (1, 1, 0)]

3. Aumentando il termine noto del primo vincolo da 4 a 4.5, qual e l’incremento che ci si aspettanel valore ottimo della funzione obiettivo ? Effettuare la verifica.

[Risultato: l’incremento e 0.5]

4. Verificare che ad un incremento del termine noto del primo vincolo oltre il valore 5 non cor-risponde nessun incremento del valore ottimo della funzione obiettivo.

5. Verificare che diminuendo il termine noto del primo vincolo a valori inferiori a 3, il valore ottimodella funzione obiettivo decresce ad una rapidita non piu proporzionale al prezzo ombra u⋆

1 = 1in quanto il punto di ottimo del problema duale (e quindi i prezzi ombra) sono cambiati.

37

Esercitazione 5

Modelli di Programmazione Lineare Intera

L’esempio che prenderemo ora in esame e un problema di gestione delle scorte (“lot sizing”) in cuii prodotti sono indivisibili e quindi e richiesto l’uso di variabili intere. Descriviamo brevemente nelseguito questo problema.

Un’impresa produce 3 prodotti (PROD1, PROD2, PROD3) nei mesi di gennaio, febbraio, marzo ed aprile.Per ciascun prodotto p, (p = 1, . . . , 3) ed in ciascun periodo t, (t = 1, . . . , 4) e nota la domanda del mercatodomandapt. Per ciascun prodotto p, gli stabilimenti dell’impresa hanno un vincolo di capacita produttiva nelmese t, definito dal coefficiente max produzpt; inoltre per ogni unita del prodotto p-esimo immagazzinata nelmese t-esimo e necessario sostenere un costo di immagazzinamento pari a cost scortept. Per la produzione diogni unita del prodotto p-esimo, l’impresa affronta un costo pari a cost produzp; infine all’inizio dell’orizzontedi pianificazione sono presenti per il prodotto p-esimo le scorte scorte inizp e si vuole che tali rimangano ancheal termine dell’orizzonte. Si costruisca il relativo modello che verifichi le specifiche, soddisfacendo esattamentela domanda del mercato e massimizzando i profitti dell’impresa e tenendo conto che i prodotti non sono frazion-abili. I dati sono riportati nelle tabelle che seguono.

cost produz scorte iniz

PROD1 5 10PROD2 3 10PROD3 2.4 10

38

domanda =

gennaio febbraio marzo aprile

PROD1 95 85 72 65PROD2 15 148 100 95PROD3 80 67 110 100

prezzo =


PROD1 13 11 10 13.5PROD2 8 9.5 8.5 10PROD3 11 10 9.5 11

max produz =


PROD1 90 80 100 60PROD2 80 120 95 75PROD3 80 80 130 80

cost scorte =


PROD1 2 2.5 3.1 1.8PROD2 1.9 2.1 1.8 1.7PROD3 2.3 2.0 1.5 1.9

Introducendo le variabili

xpt = numero di prodotti del tipo p nel periodo t (p = 1, 2, 3 t = 1, 2, 3, 4)

spt = scorte del prodotto p da effettuare nel periodo t (p = 1, 2, 3 t = 1, 2, 3, 4)

max3

∑

p=1

4∑

t=1

(prezzop,t · domandap,t − cost produzp · xp,t − cost scortep,t · sp,t)

xp,0 + scorte inizp = domandap,0 + sp,1 p = 1, 2, 3

xp,t + sp,t−1 = domandap,t + sp,t p = 1, 2, 3 t = 2, 3, 4

sp,4 = scorte inizp p = 1, 2, 3

xp,t ≥ 0 intere p = 1, 2, 3 t = 2, 3, 4

sp,t ≥ 0 intere p = 1, 2, 3 t = 2, 3, 4

Riportiamo di seguito i file .mod e .dat relativi a questa formulazione.

39

scorte.mod


set PERIODI ordered;

set PRODOTTI;


param cost_produz {PRODOTTI} >= 0;

param cost_scorte {PRODOTTI,PERIODI} >= 0;

param domanda {PRODOTTI,PERIODI} >= 0;

param prezzo {PRODOTTI,PERIODI} >=0;

param scorte_iniz {PRODOTTI} >= 0;

param max_produz {PRODOTTI,PERIODI} >=0;


var x {p in PRODOTTI, t in PERIODI} >= 0 , <= max_produz[p,t], integer;

var s {p in PRODOTTI, t in PERIODI} >= 0 , integer ;



maximize profit: sum{p in PRODOTTI, t in PERIODI}

(prezzo[p,t]*domanda[p,t]-cost_produz[p]*x[p,t]-cost_scorte[p,t]*s[p,t]);

s.t. scorte0 {p in PRODOTTI}: x[p, first(PERIODI)] + scorte_iniz[p] =

domanda[p, first(PERIODI)] + s[p, first(PERIODI)];

# vincolo per il nodo iniziale.

s.t. scorte {p in PRODOTTI, t in PERIODI : ord(t) <> 1}:

x[p,t] + s[p, prev(t)] = domanda[p,t] + s[p,t];

# vincoli per i nodi intermedi.

s.t. scorte_finali {p in PRODOTTI}: s[p,last(PERIODI)] = scorte_iniz[p];

# garantisce che le scorte finali coincidano con quelle iniziali.

40

scorte.dat

set PERIODI := gennaio febbraio marzo aprile;

set PRODOTTI:= PROD1 PROD2 PROD3;

param: cost_produz scorte_iniz :=

PROD1 5 10

PROD2 3 10

PROD3 2.4 10 ;

param domanda: gennaio febbraio marzo aprile :=

PROD1 95 85 72 65

PROD2 15 148 100 95

PROD3 80 67 110 100 ;

param prezzo: gennaio febbraio marzo aprile :=

PROD1 13 11 10 13.5

PROD2 8 9.5 8.5 10

PROD3 11 10 9.5 11 ;

param max_produz: gennaio febbraio marzo aprile :=

PROD1 90 80 100 60

PROD2 80 120 95 75

PROD3 80 80 130 80 ;

param cost_scorte: gennaio febbraio marzo aprile :=

PROD1 2 2.5 3.1 1.8

PROD2 1.9 2.1 1.8 1.7

PROD3 2.3 2.0 1.5 1.9 ;

Come si osserva dal file scorte.mod, per imporre il vincolo di interezza sulle variabili, e sufficienteinserire nella dichiarazione delle variabili la parola chiave integer; quindi per dichiarare una variabilex intera non negativa e sufficiente scrivere

var x >=0, integer ;

41

Analizziamo, ora, un modello di costo fisso che quindi richiede l’uso di varibili 0 − 1. Riportiamobrevemente la descrizione di questo problema.

(Segregated Storage Problem)E necessario immagazzinare quattro merci (Merce1, Merce2, Merce3, Merce4) all’interno di 7 silos (Silos1,Silos2, Silos3, Silos4, Silos5, Silos6, Silos7), ma in ognuno di questi silos puo trovare posto una sola merce.Di seguito si riporta una tabella che indica le quantita di merce i-esima da immagazzinare (mi), il costo cij diimmagazzinamento per tonnellata di merce i-esima, i = 1, . . . , 4 nel j-esimo silos, j = 1, . . . , 7, il costo fisso fj

associato all’utilizzo del silos j-esimo ed infine la capacita (di contenimento) di ciascun silos sj , j = 1, . . . , 7:

Silos Merce da1 2 3 4 5 6 7 immagazzinare (mi ton)

Merce 1 1 2 2 3 4 5 5 75Merce 2 2 3 3 3 1 5 5 50Merce 3 4 4 3 2 1 5 5 25Merce 4 1 1 2 2 3 5 5 80

Costo fisso silos (fj 106£) 2 4 6 8 10 12 14Capacita silos (sj ton) 25 25 40 60 80 100 100

Costruire un modello lineare che permetta la minimizzazione del costo totale derivante dall’immagazzinamento

delle merci.

Introducendo le variabili:

xij = quantita della merce i-esima che si immagazzina nel silos j-esimo(i = 1, . . . , 4 j = 1, . . . , 7)

yij =

1 se si immagazzina la merce i-esima nel silos j-esimo(i = 1, . . . , 4 j = 1, . . . , 7)

0 altrimenti,

il problema si puo formulare come

min4

∑

i=1

7∑

j=1

cijxij +7

∑

j=1

fj

4∑

i=1

yij

con i seguenti vincoli

42

4∑

i=1

yij ≤ 1 Vincoli sul numero di merci in ciascun silos (j = 1, . . . , 7)

7∑

j=1

xij = mi Vincoli di immagazzinamento merce (i = 1, . . . , 4)

xij ≤ yijM Vincoli derivanti dal costo fisso (i = 1, . . . , 4 j = 1, . . . , 7 M ≫ xij)

4∑

i=1

xij ≤ sj Vincoli sulla capacita dei silos (j = 1, . . . , 7)

xij ≥ 0 Vincoli di non negativita (i = 1, . . . , 4 j = 1, . . . , 7)

yij ∈ {0, 1} Vincoli di interezza (i = 1, . . . , 4 j = 1, . . . , 7)

Come e noto, la grandezza M e un parametro del problema e non una variabile; inoltre il valore assuntoda M deve essere non inferiore al massimo valore assunto dalle variabili xij (i = 1, . . . , 4 j = 1, . . . , 7)sopra definite.

Seguono i file .mod e .dat che realizzano una implementazione nel linguaggio di AMPL della formu-lazione riportata.

silos.mod


set MERCI;

set SILOS;


param costo_merce_silos {MERCI,SILOS} >= 0;

# l’elemento i,j di questa matrice di parametri indica

# il costo di immagazzinamento di un’unita’ di merce

# i-esima nel silos j-esimo.

param costo_fisso {SILOS} >= 0; # se un silos viene usato e’ necessario

# sostenere questo costo.

param capacita {SILOS} >= 0; # ogni silos ha una propria capacita’ di

# contenimento.

43

param merce_totale {MERCI} >=0; # per ogni merce e’ necessario immagaz-

# zinare un certo quantitativo.

param big_M := 10^5; # questa costante deve essere piu’ grande del

# massimo valore che puo’ assumere ogni componente

# del vettore x.


var x {i in MERCI, j in SILOS} >= 0; # quantita’ di merce i-sima che si

# immagazzina nel silos j-simo.

var y {i in MERCI, j in SILOS} >= 0 , binary;

# y[i,j]=1 se la merce i-sima e’ immagazzinata nel

# silos j-esimo,

# y[i,j]=0 altrimenti.



minimize costi_complessivi:

sum {i in MERCI, j in SILOS} costo_merce_silos[i,j]*x[i,j] +

sum {j in SILOS} costo_fisso[j]*sum {i in MERCI} y[i,j];

# costi variabili piu’ costi fissi.

s.t. magazzino {i in MERCI}:

sum {j in SILOS} x[i,j] = merce_totale[i];

# e’ necessario immagazzinare tutta la merce.

s.t. merci_in_silos {j in SILOS}:

sum {i in MERCI} y[i,j] <= 1;

# al piu’ in ciascun silos e’ possibile

# immagazzinare una sola merce.

s.t. vincolo_tecnico {i in MERCI, j in SILOS}:

x[i,j] <= big_M*y[i,j];

# se nel silos j-esimo non immagazziniamo la merce

# i-sima, allora la variabile x[i,j] deve essere

# nulla.

44

silos.dat

set MERCI := merce1 merce2 merce3 merce4;

set SILOS := sil1 sil2 sil3 sil4 sil5 sil6 sil7;

param costo_merce_silos:

sil1 sil2 sil3 sil4 sil5 sil6 sil7:=

merce1 1 2 2 3 4 5 5

merce2 2 3 3 3 1 5 5

merce3 4 4 3 2 1 5 5

merce4 1 1 2 2 3 5 5 ;

param: costo_fisso capacita:=

sil1 2 25

sil2 4 25

sil3 6 40

sil4 8 60

sil5 10 80

sil6 12 100

sil7 14 100 ;

param merce_totale:=

merce1 75

merce2 50

merce3 25

merce4 80 ;

Come si puo osservare dal file silos.mod, per imporre il vincolo sulle variabili yij che devono essere0 − 1, e sufficiente inserire nella dichiarazione delle variabili la parola chiave binary; quindi perdichiarare una variabile d binaria e sufficiente scrivere

var d, binary ;

Esercizio.Modificare la formulazione precedente includendo la richiesta dovuta al fatto che se nel Silos 1 c’e laMerce 3 allora nel Silos 2 non puo essere contenuta la Merce 4 e viceversa.

45

Approfondimento sull’uso degli insiemi

A conclusione di questa esercitazione vogliamo approfondire l’uso degli insiemi in AMPL. A tale scoporiprendiamo l’esempio del problema dei trasporti considerato nella Esercitazione 3 ed esaminiamo nuovielementi della sintassi di AMPL il cui uso, in alcuni casi, puo risultare molto utile. Riportiamo quindidi nuovo i file trasporto.mod e trasporto.dat con alcune varianti opportunamente commentateall’interno dei file stessi.

trasporto.mod




set NORD; # introduce l’insieme di alcune citta’ del nord Italia

set SUD; # introduce l’insieme di alcune citta’ del sud Italia

set ISOLE; # introduce l’insieme di alcune citta’ delle isole italiane








# le tre dichiarazioni che seguono sono ’simili’ nel senso che definiscono

# l’insieme COPPIE formato da coppie di elementi: uno appartenente

# ad ORIGINI e l’altro a DESTINAZIONI

#set COPPIE := {ORIGINI,DESTINAZIONI}; # queste prime due dichiarazioni

#set COPPIE:= ORIGINI cross DESTINAZIONI; # non richiedono di inserire le

# coppie di elementi nel .dat

set COPPIE within {ORIGINI,DESTINAZIONI};

#set COPPIE dimension 2; # questa dichiarazione e’ piu’ generica

# delle tre precedenti.

46


param costo_origdest {ORIGINI,DESTINAZIONI} >= 0 default 1;





# destinazioni.



# ad 1 indice. Rappresenta


# (non negativi) da ciascuna delle

# origini.



# indice. Rappresenta il numero

# (non negativo) massimo di prodotti

# che possono essere trasportati ’DA’

# ciascuna origine.



# indice. Rappresenta il numero

# (non negativo) massimo di prodotti

# che possono essere trasportati

# ’VERSO’ ciascuna destinazione.

param costo_coppie {COPPIE} >=0;

# per gli elementi (coppie di elementi)

# appartenenti all’insieme COPPIE vi

# e’ un ulteriore costo unitario di

# trasporto (per es. autostrade)

param costo_portuale; # e’ un costo unitario da imputarsi

# ad ogni unita’ di merce trasportata

# alla destinazione "olbia"


var x {i in ORIGINI,j in DESTINAZIONI} >= 0, integer ;



# numero (intero) di prodotti trasportati

# dalla origine ’i’ alla destinazione ’j’.

47





costo_origine[i]* sum{j in DESTINAZIONI} x[i,j] +

sum{(i,j) in COPPIE} costo_coppie[i,j] * x[i,j] +

sum{(i,"olbia") in {ORIGINI,DESTINAZIONI}}

costo_portuale * x[i,"olbia"];

# sum{(i,j) in {ORIGINI,DESTINAZIONI}: j="olbia"}

# costo_portuale * x[i,j];

# queste due ultime righe della funzione obiettivo

# sono del tutto equivalenti alle precedenti due




# piu’ di un determinato numero di prodotti.



# a ciascuna destinazione non e’ possibile far

# arrivare piu’ di un determinato numero

# di prodotti.

s.t. origini_nord: sum {i in ORI_NORD,j in DESTINAZIONI} x[i,j] >= 4/5 *

sum {i in ORIGINI,j in DESTINAZIONI} x[i,j] ;

# dalle citta’ di origine del nord vengono effettuati

# almeno i 4/5 dei trasporti totali.

s.t. destinazioni_isole:

sum {i in ORIGINI,j in DESTINAZIONI : j in {SUD union ISOLE}}

x[i,j] >= 2/3 * sum {i in ORIGINI,j in DESTINAZIONI} x[i,j] ;

# verso le citta’ di destinazione del sud e delle

# isole vengono effettuati almeno i 2/3 dei

# trasporti totali.

48

trasporto.dat





set NORD := asti como domodossola empoli mantova;

# l’insieme delle citta’ del nord Italia

set SUD := bari napoli;

# l’insieme delle citta’ del sud Italia

set ISOLE := olbia palermo;

# l’insieme delle citta’ delle isole d’Italia


set COPPIE : mantova napoli olbia palermo:=

asti - - - -

bergamo - + + -

como - - - -

domodossola + - - +

empoli - - + + ;

# ogni segno ’+’ indica il fatto che l’elemento (coppia) corrispondente e’

# presente nell’insieme, ogni segno ’-’ indica invece l’assenza dell’elemento.

#set COPPIE := bergamo napoli

# bergamo olbia

# domodossola mantova

# domodossola palermo

# empoli olbia

# empoli palermo ;


asti 2 100

bergamo 3 110

como 4 130

domodossola 7 85

empoli 6 120 ;

# i vettori di parametri ’costo_origine’ e ’max_uscita’ hanno

# 5 elementi (tanti quanti le origini), pertanto si possono

# fare le assegnazioni contemporaneamente

49

param domanda :=

mantova 30

napoli 18

olbia 45

palermo 56 ;

# il vettore di parametri ’domanda’ ha 4 elementi (tanti quante le

# destinazioni. Si noti che quando si assegnano gli elementi di un solo

# vettore non sono necessari i ’:’ dopo la parola chiave ’param’

#### LE SEGUENTI TRE ASSEGNAZIONI SONO EQUIVALENTI ####

#param costo_origdest (tr): asti bergamo como domodossola empoli :=

# mantova 1 1 1 1 1.7

# napoli 3.5 1 2.8 1 1

# olbia 6 4.5 4.7 1 1

# palermo 1 1 4.9 1 1 ;

#param costo_origdest : mantova napoli olbia palermo :=

# asti . 3.5 6.0 .

# bergamo . . 4.5 .

# como . 2.8 4.7 4.9

# domodossola . . . .

# empoli 1.7 . . . ;


asti 1 3.5 6.0 1

bergamo 1 1 4.5 1

como 1 2.8 4.7 4.9

domodossola 1 1 1 1

empoli 1.7 1 1 1 ;

# la matrice di parametri ’costo_origdest’ contiene 4*5 = 20 elementi, uno per

# ogni coppia origine/destinazione. Non e’ necessario specificare lo ’0’

# davanti alla virgola e le componenti ’.’ per default valgono 1 (vedi .mod).

param: costo_coppie :=

bergamo napoli 2

bergamo olbia 3.5

domodossola mantova 0.5

domodossola palermo 3.8

empoli olbia 3.5

empoli palermo 3.1 ;

# le possibili coppie origine/destinazione sono 5*4 = 20 ma

# l’insieme COPPIE ne contiene solo 6;

50

param costo_portuale := 0.1 ;

# per ogni merce che ha come destinazione

# "olbia" vi e’ questo costo aggiuntivo;

51

Esercitazione 6

Programmazione Lineare Intera

In questa esercitazione si vuole considerare la tecnica del “Branch and Bound” per risolvere problemidi Programmazione Lineare Intera. In particolare, si vuole utilizzare AMPL come strumento perrisolvere i vari sottoproblemi di Programmazione Lineare (problemi rilassati) che forniscono “lowerbound ” in un problema di minizzazione o “upper bound” in un problema di massimizzazione dellasoluzione ottima intera di ogni sottoproblema. Naturalmente il solutore lineare di AMPL e in grado dirisolvere direttamente un problema di Programmazione Lineare Intera e quindi la soluzione ottenutacon la tecnica del “Branch and Bound” sara poi confrontata con quella ottenuta direttamente.A questo scopo consideriamo il seguente problema di Programmazione Lineare Intera1

(Prob 0)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 11 ≤ x1 ≤ 40 ≤ x2 ≤ 3x1, x2 interi

E un problema di massimizzazione, quindi le soluzioni dei problemi rilassati forniranno dei limitisuperiori (“upper bounds”) al valore della soluzione ottima intera. Inoltre, il valore della funzioneobiettivo calcolato in corrispondenza ad una soluzione ammissibile fornira una limitazione inferiore.

• Implementare e risolvere con AMPL il rilassamento lineare del (Prob 0). •

La soluzione ottima x(0) del rilassamento lineare di (Prob 0) e x(0) =

(

7/317/6

)

e fornisce un “upper

bound” pari a U0 = x(0) = 59/6 = 9.8333 . . ..Se effettuiamo un semplice arrotondamento all’intero inferiore delle componenti di x(0) otteniamo il

vettore

(

22

)

. Poiche tale vettore e ammissibile per (Prob 0), possiamo porre come prima soluzione

ammissibile x =

(

22

)

e quindi possiamo inizializzare l’ottimo corrente z con il valore corrispondente

cioe z = 8 (che e una limitazione inferiore dell’ottimo del problema intero).

1cfr. A. Sassano, Metodi e Modelli della Ricerca Operativa, FrancoAngeli, 1999.

52

Non e possibile chiudere il problema (Prob 0) in quanto la soluzione x non e intera e l’“upper bound”e strettamente maggiore di z. Il problema viene quindi inserito nella lista L dei problemi candidati.Viene selezionato un problema in L = {(Prob 0)}. In particolare, viene estratto dalla lista il problema(Prob 0). Si procede quindi alla separazione del problema (Prob 0). Possiamo separare rispetto aduna qualsiasi delle variabili non intere, per semplicita decidiamo di separare rispetto alla variabile conindice piu piccolo (x1). A tale scopo, aggiungiamo ai vincoli della formulazione di (Prob 0), i due

vincoli x1 ≥ ⌈x(0)1 ⌉ e x1 ≤ ⌊x

(0)1 ⌋ cioe x1 ≥ 3 e x1 ≤ 2.

Si ottengono i due problemi seguenti :

(Prob 1)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 11 ≤ x1 ≤ 20 ≤ x2 ≤ 3x1, x2 intere

(Prob 2)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 13 ≤ x1 ≤ 40 ≤ x2 ≤ 3x1, x2 intere

• Risolvere con AMPL il rilassamento lineare di questi due problemi. •

Il rilassamento lineare del problema (Prob 1) ha soluzione x(1) =

(

25/2

)

e il corrispondente valore

U1 = 8.5. La soluzione del rilassamento lineare del problema (Prob 2) e, invece, x(2) =

(

31/2

)

con

valore U2 = 9.5.Entrambi i problemi non sono eliminabili e vengono quindi inseriti nella lista L.

Viene scelto un problema nella lista L = {(Prob 1), (Prob 2)} dei problemi candidati. In particolareesaminiamo il problema (Prob 1).La prima componente di x(1) e intera mentre la seconda componente e frazionaria. Scegliamo quindila variabile x2 per effettuare la separazione. A tale scopo, aggiungiamo alla formulazione di (Prob 1)i due vincoli x2 ≤ 2 e x2 ≥ 3 . In tal modo, otteniamo i due problemi seguenti :

(Prob 3)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 11 ≤ x1 ≤ 20 ≤ x2 ≤ 2x1, x2 intere

(Prob 4)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 11 ≤ x1 ≤ 23 ≤ x2 ≤ 3x1, x2 intere


La soluzione del rilassamento lineare del problema (Prob 3) e x(3) =

(

22

)

ed ha valore U3 = 8.

Il problema (Prob 4), invece, non ha soluzioni ammissibili. Di conseguenza, poniamo U4 = −∞.E possibile chiudere sia il problema (Prob 3) sia il problema (Prob 4). Il primo in quanto la soluzionedel rilassamento lineare e intera, il secondo in quanto non ha soluzione ammissibili (ovvero poicheU4 < z). Nessuno dei due viene quindi inserito nella lista L.

53

Si osservi che, pur essendo x(3) una soluzione intera, non aggiorniamo l’ottimo corrente in quantox = x(3).

Estraiamo dalla lista L = {(Prob 2)} il problema (Prob 2) (unico problema rimasto) ed effettuiamo laseparazione rispetto alla variabile x2 (infatti la seconda componente di x(2) e frazionaria). Dobbiamoaggiungere alla formulazione di (Prob 2) i due vincoli x2 ≤ 0 e x2 ≥ 1 . In tal modo, otteniamo i dueproblemi seguenti :

(Prob 5)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 13 ≤ x1 ≤ 40 ≤ x2 ≤ 0x1, x2 intere

(Prob 6)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 13 ≤ x1 ≤ 41 ≤ x2 ≤ 3x1, x2 intere



(

3.14 . . .0

)

ed ha valore U5 =

9.428 . . ..Il problema (Prob 6), invece, non ha soluzioni ammissibili. Di conseguenza, poniamo U6 = −∞.Il problema (Prob 6) viene chiuso in quanto non ha soluzione ammissibili, il problema (Prob 5) none eliminabile e va quindi inserito nella lista L. Infatti il suo valore ottimo e pari a 9.428 . . ., e poichetale valore e migliore di quello della soluzione intera trovata (ossia 8), il problema non e eliminabile(nella sua regione ammissibile potrebbe trovarsi una soluzione intera migliore di quella corrente).

Nella lista L vi e ora solo il problema S5, che viene quindi scelto. Viene effettuata la separazionerispetto alla variabile x1. A tale scopo, si aggiungono alla formulazione di (Prob 5) i due vincolix1 ≤ 3 e x1 ≥ 4 , ottenendo i due problemi:

(Prob 7)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 13 ≤ x1 ≤ 30 ≤ x2 ≤ 0x1, x2 intere

(Prob 8)

max 3x1 + x2

7x1 + 2x2 ≤ 22−2x1 + 2x2 ≤ 14 ≤ x1 ≤ 40 ≤ x2 ≤ 0x1, x2 intere



(

30

)

ed ha valore U7 = 9.

Il problema (Prob 8), invece, non ha soluzioni ammissibili. Di conseguenza, poniamo U8 = −∞.I problemi (Prob 7) e (Prob 8) possono essere chiusi: il primo in quanto la soluzione ottenuta e intera,il secondo in quanto non ha soluzione. La soluzione intera di (Prob 7) e migliore di quella corrente e

quindi la soluzione corrente viene aggiornata (si pone x =

(

30

)

).

54

La lista L e ora vuota, il procedimento quindi termina. La soluzione ottima e data dalla soluzionecorrente, ossia dalla soluzione del problema S7:I vari passi della procedura di soluzione possono essere schematizzati utilizzando il cosiddetto Albero

di Enumerazione riportato in Figura 2.

0

1 2

3 654

7 8

Figura 2: Albero di enumerazione.

In tale albero i nodi indicano i problemi mentre i rami stabiliscono le relazioni padre-figlio (generatore-generato) nel processo di generazione.

Esercizio. Utilizzando AMPL per risolvere i problemi rilassati, applicare la tecnica del “Branch andBound” per risolvere il seguente problema di Programmazione Lineare 0–1:

max−100x1 + 72x2 + 36x3

−2x1 + x2 ≤ 0−4x1 + x3 ≤ 0x1 + x2 + x3 ≥ 1x1 ∈ {0, 1}, x2 ∈ {0, 1}, x3 ∈ {0, 1}.

Si ricorda che, poiche le variabili devono assumere valori 0–1, si puo sempre supporre che la formu-lazione del problema sia contenuta nell’ipercubo unitario

{x ∈ IRn | 0 ≤ x1 ≤ 1, i = 1, . . . , n}

e quindi ogni componente xh dell’ottimo del problema rilassato e tale che 0 ≤ xh ≤ 1. Questo implicache i sottoproblemi eventualmente generati nella separazione si otterrano ponendo xh = 0 in uno exh = 1 nell’altro.

55

Approfondimento sull’uso dei parametri

In alcuni casi puo essere molto utile rendere ancora piu flessibile la scrittura di un modello in AMPLintroducendo dei parametri che sostanzialmente possono essere dichiarati come “parametri variabili”il cui valore e assegnato nel file .dat. Questo puo essere realizzato utilizzando la parola chiavesymbolic che puo essere associata alla dichiarazione dei parametri. Vediamo un semplice esempiodi cio considerando un modello di Programmazione Lineare basato su un modello gia visto (cfr.Esempio 2.2.2 delle “Lezioni di Ricerca Operativa”) del quale riportiamo brevemente una descrizione.

Una azienda automobilistica produce tre diversi modelli di autovettura: un modello economico, uno normale eduno di lusso. Ogni autovettura viene lavorata da tre robot: A, B e C. I tempi necessari alla lavorazione sonoriportati, in minuti, nella tabella seguente insieme al profitto netto realizzato per autovettura

Economica Normale Lusso

A 20 30 62B 31 42 51C 16 81 10

Prezzo 1000 1500 2200

I robot A e B sono disponibili per 8 ore al giorno mentre il robot C e disponibile per 5 ore al giorno. Il

numero di autovetture di lusso prodotte non deve superare il 20% del totale mentre il numero di autovetture

economiche deve costituire almeno il 40% della produzione complessiva. Se si produce piu del 50% di autovetture

economiche, allora c’e da pagare una penale pari a 10000. Supponendo che tutte le autovetture vengano vendute,

formulare un problema di Programmazione Lineare che permetta di decidere le quantita giornaliere da produrre

per ciascun modello in modo tale da massimizzare i profitti rispettando i vincoli di produzione. (Si supponga

di formulare il problema in maniera tale che i prezzi possano essere scalati (divisi) di una quantita data sotto

forma di parametro.)

Indichiamo con x1, x2, x3, rispettivamente il numero di autovetture del modello economico, normale edi lusso da produrre giornalmente e con δ ∈ {0, 1} una variabile binaria cosı definita:

δ =

{

1 se si produce piu del 50% di autovetture economiche0 altrimenti

Con questa scelta delle variabili una formulazione del problema e la seguente:

max (1000x1 + 1500x2 + 2200x3)20x1 + 30x2 + 62x3 ≤ 48031x1 + 42x2 + 51x3 ≤ 48016x1 + 81x2 + 10x3 ≤ 300x3 ≤ 0.2 (x1 + x2 + x3)x1 ≥ 0.4 (x1 + x2 + x3)x1 − 0.5(x1 + x2 + x3) ≤ Mδx1 ≥ 0 x2 ≥ 0 x3 ≥ 0δ ∈ {0, 1}.

56

Si riportano di seguito i file autovetture.mod e autovetture.dat che implementano questo problemafacendo uso della parola chiave symbolic.

autovetture.mod

#### SEZIONE DEFINIZIONE SET ####

set AUTOVETTURE ;

set ROBOT;

#### SEZIONE DEFINIZIONE E TEST PARAMETRI #####

param par1 symbolic in AUTOVETTURE; # i parametri ’par1’ e ’par2’

param par2 symbolic in AUTOVETTURE; # sostanzialmente vengono di-

# chiarati come parametri "va-

# riabili", il cui valore viene

# poi assegnato nel file .dat .

# Le due dichiarazioni sopra insieme

# con le assegnazioni fatte nel

# file .dat sono equivalenti a

# sostituire nella formulazione

# "lusso" a ’par1’ e "economica" a

# ’par2’.

param prezzi{AUTOVETTURE}>=0; # array dei prezzi per le vetture

param dispo_max{ROBOT}>=0; # disponibilita’ oraria robot

param rich_tempo{ROBOT,AUTOVETTURE}>=0 , integer;

# questa matrice di parametri con-

# tiene le necessita’ di tempo per

# ogni autovettura su ciascun robot

param perc_max_lusso >=0; # percentuale macchina di lusso

param perc_min_economica >=0; # percentuale macchina economica

param scalatura >0; # % di scalatura dei prezzi

param big_M:= 10^6;

57

#### SEZIONE DICHIARAZIONE VARIABILI ####

var x{AUTOVETTURE}>=0, integer;

var delta >=0, binary;

#### SEZIONE VINCOLI & FUNZ. OBIETTIVO ####

maximize profitto: sum{j in AUTOVETTURE} prezzi[j]/scalatura*x[j] -

10000*delta;

s.t. v_min_robot {i in ROBOT}: sum{j in AUTOVETTURE}

rich_tempo[i,j]*x[j] <= dispo_max[i];

# vincolo sulla disponibilita’ di

# tempo per i tre tipi di robot

s.t. max_lusso : x[par1] <= perc_max_lusso *

(sum{j in AUTOVETTURE} x[j]);

# vincolo sulla percentuale massima

# di macchine di lusso

s.t. min_economiche : x[par2]>= perc_min_economica *

(sum{j in AUTOVETTURE} x[j]);

s.t. penalita: x[par2] - .5*sum{j in AUTOVETTURE} x[j] <=

big_M*delta;

58

autovetture.dat

set AUTOVETTURE := economica normale lusso;

set ROBOT := A B C;

param par1 := lusso; # al parametro ’lusso’ viene assegnata

# la stringa (valore) ’’lusso’’

param par2 := economica; # per il parametro ’economica’ vale lo

# stesso discorso.

param: prezzi :=

economica 1000

normale 1500

lusso 2200 ;

param: dispo_max :=

A 480

B 480

C 300 ;

param rich_tempo : economica normale lusso :=

A 20 30 62

B 31 42 51

C 16 81 10 ;

param perc_max_lusso := 0.2;

param perc_min_economica := 0.4;

param scalatura := 1;

59

UNIVERSITA di ROMA “LA SAPIENZA”` Corso di Laurea in Ingegneria Informatica...

Documents

Transcript of UNIVERSITA di ROMA “LA SAPIENZA”` Corso di Laurea in Ingegneria Informatica...