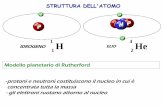
L'atomo

Entità subatomiche Carica elettrica Massa (u.m.a)

ProtoneNeutroneelettrone

+1e0

-1e

1.00731.0087

5.48•10-4

e = Carica elettrica elementare 1.6022•10-19 Coulombu.m.a.= Unità di Massa Atomica 1.6605•10-24 grammi

Il Nuclide

NuAZZ (numero atomico) = n° di protoni

A (numero di massa) = n° di protoni + n° di neutroni

Isotopi sono i nuclidi che hanno uguale numero atomico ma diverso numero di massaElementi sono i nuclidi che hanno diverso numero atomico, a questi è stato dato un nome e sono rappresentati da simboli

M. Pasquali

La configurazione elettronica

. Modello atomico di Bohr-Sommerfeld (1913)

Legge fondamentale della meccanica classica F = m a

F Coulomb = 1 4 πε° . q q '

r 2 F centrifuga = mv 2 r

ε°=8.85*10-12 Fm-1 (costante dielettrica del vuoto)

e 2 r 2

= m v 2 r r = e 2

m v 2

v = e m r

e 2 r 2

= m v 2 r (1)

Quantizzazione del momento angolare

mvr = n h 2 π (2)

h=6.626*10-34 J sec

M. Pasquali

Quantizzazione del raggio delle orbite

mvr = n h 2 π

Dalla (2)

r = nh2 π mv

→ r 2 = n 2 h 2

4 π 2 m 2 v 2

e 2 r 2

= m v 2 r Sostituendo nella (1)

r = n 2 h 2

4 π 2 m e 2 dove n = 1, 2, 3, 4, ..

M. Pasquali

Quantizzazione dell'Energia

E = E cin. + E pot. = 1 2 mv 2 - e 2 r

Dalla (1) da cui si ha:rvm

re 2

2

2

= remv

22 =

E = 1 2

e 2 r - e 2 r = -

1 2

e 2 r essendo i raggi quantizzati in base alla relazione:

r = n 2 h 2

4 π 2 m e 2 dove n = 1, 2, 3, 4, .

E n = - 1 n 2 2 π 2 m e 4

h 2 M. Pasquali

Raggi delle orbite corrispondenti ai primi quattro stati quantici dell’elettrone dell’atomo di idrogeno secondo il modello di Bohr

Livelli energetici corrispondenti ai primi stati quantici dell’elettrone dell’atomo di idrogeno secondo il modello di Bohr

2

42

2n h me2π

n1E ∗−=

me4π hnr 22

22

n ∗=

M. Pasquali

N. Bohr si rese conto che l’emissione di luce da parte degli atomi doveva avere a che fare con gli elettroni, che ruotavano intorno al nucleo

- Per saltare da un’orbita ad un’altra di livello energetico più alto, l’elettrone deve assorbire energia

- Quando l’elettrone cade su un livello di energia inferiore, l’atomo emette una luce caratteristica (emette energia)

- L’energia della luce emessa o assorbita è uguale alla differenza fra le energie delle due orbite

M. Pasquali

A

Aλ

λ

distanza del massimo di una cresta dal livello corrispondente alla posizione di quieteA = Ampiezza;

Distanza tra i due massimi di due creste consecutive ovvero tra due punti in faseλ = Lunghezza d’onda;

Spazio percorso da una cresta in un dato intervallo di tempo

Numero di creste (n) che in un determinato intervallo di tempo (t) passano per un punto dato

v = Velocità;

ν = frequenza;

t'1

nt1 ν ==)sec (dim.

tn ν 1-= t’ = tempo necessario per il transito di 1 λ

λv ν

ondad' lunghezza nepropagazio di velocitàfrequenza =→=λν

t'λ

t'ondad' lunghezza v ===

M. Pasquali

λc ν =

Velocità della luce:

c = λ · ν = 3 ·108 m s-1M. Pasquali

Ogni radiazione può essere considerata come un insieme di numerosissime particelle, dette fotoni, ognuna con il suo determinato pacchetto di energia

M. Pasquali

M. Pasquali

Spettri atomici

Spettro a righe dell’idrogeno

Ogni atomo emette uno spettro caratteristico formato da una serie di righe

Gli spettri atomici si possono usare come un’impronta digitale per riconoscere gli elementi

M. Pasquali

λc ν =hν ε =

Transizione elettroniche nell’eccitazione di un atomo per assorbimento di energia

a) Una riga spettrale di frequenza ν (secondo Bohr) b) doppietto di frequenze ν0 e ν1 (secondo Sommerfeld

M. Pasquali

ε = hν

ν = c/λ

ε = h c/λ

c = 3 ·108 m s-1

Transizioni elettroniche e serie di righe caratteristiche dello spettro dell’atomo d’idrogeno.

M. Pasquali

n = 1, 2, 3, 4, …..n (numero quantico principale) l = 0, 1, 2, 3, ….(n-1) (numero quantico angolare) m = 0, ±1, ±2, ±3 … ±l (numero quantico magnetico) Ms = ± ½ (numero quantico di spin)

M. Pasquali

Esperienza di Davison e Germer

Per i fotoni Planck – Einstein avevano scritto:

mch λ

mc λ

hc λc ν essendo ed mc hν ε

2

2

=

=

===

Le onde di De Broglie

vm h λ =

Diffrazione di un fascio di raggi luminosi al passaggio attraverso un piccolo foro (a,b) e diffrazione di un fascio di raggi X (c,d) e di un fascio di elettroni (c,e) al passaggio attraverso una sottile foglia di argento policristallino

h = costante di Planck 6.626*10-34 j sec λ = lunghezza d’onda m = massa v = velocità

M. Pasquali

Onde di De Broglie associate a diversi tipi di particelle

mv

hλ = In cui h= 6.6262*10-34 j sec

Particella m (g) v cm/sec λ (Ǻ)Elettrone lento 9.1*10-28 1 7.3*108

Elettrone lento 9.1*10-28 100 7.3*106

Elettrone accelerato da 100 Volt 9.1*10-28 5.9*108 1.2Elettrone accelerato da 10000 Volt 9.1*10-28 5.9*109 0.12Protone accelerato da 100 Volt 1.67*10-24 1.38*107 0.029Molecola di H2 a 200 °C 3.3*10-24 2.4*105 0.82Particella α emessa da un nucleo di Ra 6.6*10-24 1.51*109 6.6*10-5

Sfera di 1/1000 di mg (1µg), v = 1cm/sec 10-6 1 6.6*10-13

Sfera di 1g alla velocità di v = 1cm/sec 1 1 6.6*10-19

M. Pasquali

Equazione di Schrödinger (1927)

Equazione che descrive la propagazione di un onda è:

2

2

22

2

2

2

2

2

δtfδ

v1

δzfδ

δyfδ

δxfδ

=++

(equazione generale delle onde)f è una funzione delle coordinate x, y, z e del tv è la velocità di propagazione dell'onda

Le onde associate agli elettroni nel loro movimento intorno al nucleo sono onde stazionarie.

0ψλ

4πδzψδ

δyψδ

δxψδ

2

2

2

2

2

2

2

2

=+++

Dove ψ è la funzione d’onda e λ è la lunghezza d’onda. Usando la relazione di De Broglie (λ=h/mv), e dal momento che l’equazione d’onda permette di calcolare i valori degli stati energetici dell’atomo e quindi Etot= Ecin+ Epot1/2mv2 = Etot – Epot si ha

M. Pasquali

0ψ )E-(Eh

8πδzψδ

δyψδ

δxψδ

pottot2

2

2

2

2

2

2

2

=+++m

Dal punto di vista matematico esistono infinite funzioni d'onda (Y) che sono soluzioni dell'equazione di Schrödinger, ma dal punto di vista fisico solo alcune di queste possono essere accettate e cioè:

ψ Deve essere continua e finita ad un solo valore in ogni punto dello spazio e all'infinito tende a zero

1)

ψ Deve soddisfare alla condizione di normalizzazione, cioè la probabilità di trovare l’elettrone, in tutto lo spazio attorno al nucleo, deve essere unitaria

2)

∫∫∫ =z

2

yx

1dVψ

M. Pasquali

Tabella delle funzioni ψn l m ms

M. Pasquali

Punto di contatto tra la teoria ondulatoria e la teoria Bohr

nλ = 2πr

Introducendo la relazione di De Broglie

mv

hλ =

r π2 mv

hn =

Da cui

π2

hn mvr =

Quantizzazione di BohrM. Pasquali

Orbitale di tipo s (n = 1,2,3… ; l = 0 ; m = 0)

La funzione orbitale ϕ in un piano

La probabilità di trovare l’elettrone entro una sfera di raggio r è pari a:

∫=r

0

22 drΨ4ππP

Superficie di contorno per un valore costante della funzione

Orbitale di tipo p (n = 2,3… ; l = 1 ; m = -1, 0, +1)

La funzione 2 pz in un piano passante per l’asse z

Superficie di contorno per un valore costante della funzione px , py , pz ,

xy

z

x xy y

z z

ml=0

ml=+1 ml=-1

Orbitale di tipo d (n = 3,4… ; l = 2 ; m = -2, -1, 0, +1, +2)

ml=+2

ml=-2

z

z

y

y

x

xml=+1

ml=-1

z

z

y

y

x

x

ml=0

z

yx

Superficie di contorno per un valore costante della funzione d z2 , d xz , d yz , d xy e d x2-y2

ml=0

ml=+1

ml=-1

ml=+2

ml=-2

ml=+3

ml=-3

Orbitale di tipo f

ml=o

ml=+1ml=-1 ml=+2 ml=-2

ml=+3ml=-3 ml=+4

ml=-4

Orbitale di tipo g

Schema di successione dei livelli energetici degli orbitali la cui progressiva saturazione determina la configurazione elettronica degli elementi nel loro stato fondamentale (non in scala)

1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s

Costruzione della configurazione elettronica dei vari atomiZ Simbolo Conf.Elettronica Simbolismo1 H 1s1 ↑2 He 1s2 ↑↓ = [He]

3 Li 1s2 2s 1 oppure [He]2s1 [He] ↑

4 Be [He]2s2 [He] ↑↓

5 B [He]2s22p1 [He] ↑↓ ↑

6 C [He]2s22p2 [He] ↑↓ ↑ ↑

7 N [He]2s22p3 [He] ↑↓ ↑ ↑ ↑

8 O [He]2s22p4 [He] ↑↓ ↑↓ ↑ ↑

9 F [He]2s22p5 [He] ↑↓ ↑↓ ↑↓ ↑

↑↓ ↑↓ ↑↓ ↑↓10 Ne [He]2s22p6 [He] = [Ne]

11 Na 1s2 2s22p6 oppure [Ne]2s1 [Ne] ↑

12 Mg [Ne]3s2 [Ne] ↑↓

13 Al [Ne]3s23p1 [Ne] ↑↓ ↑

14 Si [Ne]3s23p2 [Ne] ↑↓ ↑ ↑

15 P [Ne]3s23p3 [Ne] ↑↓ ↑ ↑ ↑

16 S [Ne]3s23p4 [Ne] ↑↓ ↑↓ ↑ ↑

17 Cl [Ne]3s23p5 [Ne] ↑↓ ↑↓ ↑↓ ↑

↑↓ ↑↓ ↑↓ ↑↓18 Ar [Ne]3s23p6 [Ne] = [Ar]

Z Simbolo Conf.Elettronica Simbolismo

19 K 1s2 2s22p6 3s23p6 4s1 oppure [Ar]4s1 [Ar] ↑

20 Ca [Ar]4s2 [Ar] ↑↓

21 Sc [Ar] 4s23d1 [Ar] ↑↑↓

↑↓ ↑ ↑

↑↓ ↑ ↑ ↑

↑↓ ↑ ↑

22 Ti [Ar] 4s23d2 [Ar]

↑

↑↓ ↑ ↑ ↑

↑↓ ↑↓ ↑ ↑

23 V [Ar] 4s23d3 [Ar]

24 Cr [Ar] 4s23d4 [Ar] ↑

25 Mn [Ar] 4s23d5 [Ar] ↑ ↑

26 Fe [Ar] 4s23d6 [Ar] ↑ ↑

27 Co [Ar] 4s23d7 [Ar]

↑

↑ ↑

↑ ↑ ↑

↑↓ ↑ ↑

↑↓ ↑↓ ↑

↑↓ ↑↓ ↑↓

↑↓ ↑↓ ↑↑↓ ↑ ↑

↑↓ ↑↓28 Ni [Ar] 4s23d8 [Ar] ↑↑↓ ↑↓ ↑

29 Cu [Ar] 4s23d9 [Ar] ↑↓ ↑↓ ↑↓ ↑↓ ↑↑↓

30 Zn [Ar] 4s23d10 [Ar] ↑↓ ↑↓ ↑↓ ↑↓ ↑↓↑↓

31 Ga [Ar] 4s23d10 4p1 [Ar]

32 Ge [Ar] 4s23d10 4p2 [Ar]

33 As [Ar] 4s23d10 4p3 [Ar]

34 Se [Ar] 4s23d10 4p4 [Ar]

35 Br [Ar] 4s23d10 4p5 [Ar]

36 Kr [Ar] 4s23d10 4p6 [Ar]

↑↓ ↑↓ ↑↓↑↓ ↑↓ ↑↓

↑↓ ↑↓ ↑↓↑↓ ↑↓ ↑↓

↑↓ ↑↓ ↑↓↑↓ ↑↓ ↑↓

↑↓ ↑↓ ↑↓↑↓ ↑↓ ↑↓

↑↓ ↑↓ ↑↓↑↓ ↑↓ ↑↓

↑↓ ↑↓ ↑↓ ↑↓ ↑↓↑↓

Variazione dei livelli energetici degli orbitali atomici al crescere del numero atomico Z (non in scala)

Tavola Periodica degli Elementi

Legenda

Solidi Liquidi Gas Artificiali

Metalli Alcalini Metalli alcalino terrosi Metalli di Transizione Terre Rare

Altri metalli Gas nobili Alogeni Non metalli

La linea rossa divide i metalli (in basso a sinistra) da i non metalli (in alto a destra).

Dimensioni relative di alcuni atomi e ioni (in nanometri nm)

Per i metalli sono indicati i raggi degli atomi.