Presentazione -...
Transcript of Presentazione -...
Almanacco MaddMaths! 2013 di Redazione MaddMaths! è distribuito con Licenza Creative Commons Attribuzione - Non commerciale - Condividi allo stesso modo 4.0 Internazionale. Il racconto “Revolutionine” di Diego Altobelli © Diego Altobelli | www.revolutionine.com, è rilasciato sotto licenza Creative Commons Attribution Non Commercial No Derivs 2.5
Presentazione
2013, un anno di grande trasformazione per MaddMaths!, sia nella forma, abbiamo cambiato piattaforma passando da Plone a WordPress, che come contenuti. La presenza dell’Unione Matematica Italiana ha creato l’opportunità per occuparci di nuove tematiche non si era mai parlato così tanto di numeri primi e lanciare iniziative di grande richiamo, prima fra tutte le due dirette dalle Olimpiadi della Matematica, che hanno visto un grande successo di partecipazione.
Poi chiaramente è stato l’anno di Comics & Science, che ha richiamato sul sito e dal vivo tantissime persone. Gli eventi con al Festival della Scienza di Genova e a Lucca Comics & Games, la vendita della pubblicazione online e nelle librerie, hanno richiamato sul sito un numero molto grande di lettori. Gli accessi al sito sono più che raddoppiati e il nostro gruppo Facebook ha superato il migliaio di partecipanti. Il sito ebuzzing http://labs.ebuzzing.it/, ci mette al 21esimo posto nel mese di dicembre tra i siti scientifici italiani, e al secondo posto per la matematica. Crediamo sia un bel risultato per noi e per tutti coloro che hanno collaborato a questa iniziativa.
Con questo Almanacco riprendiamo una tradizione che ci aveva accompagnato negli anni passati. Vi proponiamo infatti una piccola selezione degli articoli che hanno avuto maggior successo durante l’anno appena passato, in formati (pdf, epub, azw3) che vi permetteranno, speriamo, una più agevole lettura offline (addirittura stampato su carta!). Buona lettura e a presto sul sito!
* CopertinaPresentazioneGennaio
Il test di ProustLucia Caporaso
FantamatematicaIsaac “Mad Dog” Newton – Parte I di Stefano Pisani
FebbraioI luoghi della matematica
[#15] EMS 2012: Un matematico al Congresso di Camillo De LellisGiugno
L’Alfabeto della MatematicaT come Trasformata di Corrado Mascia
FantamatematicaGauss il genio timido di Stefano Pisani
FocusLa matematica delle impronte digitali di Riccardo Aragona, Massimiliano Sala e ClaudiaTinnirello
Giovani Matematici cresconoMassimiliano Gubinelli e le equazioni alle derivate parziali con rumori molto singolari, di MayaBriani
Luglio* Cédrat Villani di Leo OrtolaniSulle tracce del mostro
Settembre“L’America dimenticata” – Intervista a Lucio RussoAngolo Arguto
A che serve la matematica? La domanda dalle cento risposte, a cura di Kees PopingaOttobre
* I Want you for Comics & Science di Leo OrtolaniUno strepitoso post di Andrea Plazzi apparso sul blog di Leo OrtolaniConsistenza matematica, una storia abbastanza complicata di Roberto Natalini
NovembreI luoghi della matematica
[#16] Matematica & Informatica Lo Heidelberg Laureate Forum: dove i pulcini incontrano iCampioni di Leandro Arosio
Materiali didatticiDifficoltà in matematica: la diagnosi di ‘atteggiamento negativo’ di Rosetta Zan
DicembreRevolutionine di Diego Altobelli, illustrazione di Emmanuele RossoPerché l’ho fatto? Leo Ortolani ci racconta perché ha scritto Misterius
Il test di ProustAlla fine del XIX secolo, l’adolescente Marcel Proust scopre in un libro inglese della sua amica Antoinette Faure il test passato alla storia come “questionario di Proust”, una serie di domande varie su gusti e aspirazioni. Abbiamo modificato le domande del test ‘in senso matematico’: di seguito, i matematici rispondono al ‘Test di Proust math reloaded’.
Lucia CaporasoLucia Caporaso è Ordinario di Geometria all’Università degli Studi Roma Tre e cocoordinatrice del nostro sito.
1. Il tratto principale del mio essere matematicoPensare pensare pensare.
2. La qualità che desidero in un matematicoEleganza e originalità.
3. La qualità che preferisco nella matematicaL’universalità.
4. Quel che apprezzo di più nei miei colleghi matematiciSemplicità e onestà.
5. Il mio principale difetto come matematicoL’impazienza.
6. La mia lettura matematica preferitaGli scritti di David Mumford.
7. Il mio sogno come matematicoLa matematica vista dai giovanissimi come quel bel gioco che è.
8. Qual è la principale debolezza della matematicaL’intransigenza: ammette errori solo quando vuole misurarli.
9. Il matematico che vorrei essereAlbert Einstein.
10. Il paese in cui vorrei vivereUn paese bello come l’Italia, stimolante come gli Stati Uniti, civile come l’Inghilterra, affascinante come l’India.
11. L’esercizio matematico che preferiscoCostruire esempi e controesempi.
12. Il teorema che amoQuello che sto cercando di dimostrare. Il mio primo amore risale all’infanzia: il teorema di Pitagora.
13. L’applicazione della matematica che preferiscoLe applicazioni all’astronomia, da Eratostene in poi.
14. I matematici che mi hanno indirizzato
Il mio relatore di tesi di laurea, Enrico Arbarello: mi ha indirizzato negli Stati Uniti a studiare per il dottorato, oltre che nella matematica.
15. I matematici che mi hanno dissuasoNessun matematico mi ha mai dissuaso, però ogni tanto ci prova qualche ministro italiano.
16. Il nome della variabile che preferiscoNon ho preferenze, mi piace sceglierli e organizzarli a seconda della situazione.
17. Il tipo di calcolo che preferiscoHo un debole per i limiti di successioni e serie numeriche.
18. Il tipo di calcolo che utilizzo di piùIl semplice calcolo con le quattro operazioni, travestito da sembrare astrusissimo.
19. Il tipo di calcolo che mi annoia maggiormenteQuello dei soldi.
20. I nomi che preferisco (teorema, corollario, lemma…)Teorema.
21. Quel che detesto più di tuttoDetesto certi anglicismi d’uso comune in matematica, il peggiore è”triviale” invece di “banale”.
22. I matematici che disprezzo di piùQuelli che pretendono di usare la matematica per imporre le loro opinioni personali (politiche, sociali, religiose…).
23. L’impresa scientifica che ammiro di piùLe teorie della relatività di Einstein.
24. La riforma culturale che apprezzo di piùL’introduzione della scuola dell’obbligo.
25. Il dono di natura che vorrei avereL’orecchio musicale assoluto.
26. Da matematico, come vorrei essere ricordatoBene.
27. Stato attuale dei miei studiPiù passa il tempo e più ho da imparare.
28. Gli errori che mi ispirano maggiore indulgenzaQuelli degli altri.
29. Il mio mottoFatti non foste a viver come bruti ma per seguir virtute e conoscenza.
Luoghi comuni, curiosità et alia1. Perché la matematica dovrebbe descrivere l’universo?La matematica è un linguaggio e quindi può descrivere anche l’universo. Il bello è che lo fa in modo universale, privo da vincoli culturali. Mi viene in mente un film di fantascienza nel quale gli extraterrestri per comunicare con gli umani in mancanza di un linguaggio comune utilizzano alcune famose successioni di numeri (quella di Fibonacci e quella dei numeri primi).
1b. Lei ha descritto l’universo? E cosa in particolare?Qualche atomo, anzi qualche quark.
2. Perché la ricerca matematica è uomo?2b. Dove sono finite le donne?Domanda sbagliata, fatta alla persona sbagliata.
3. La matematica applicata cresce alla stessa velocità dei software matematici?I software non sono forse parte della matematica applicata? Quindi la matematica applicata cresce almeno altrettanto velocemente.
3b. Quale funzione potrebbe modellizzare la crescita del settore della matematica di cui si occupa?Domanda difficile … una funzione con moltissime variabili.
4. Quanto conta lo studio nella risoluzione di grosse questioni matematiche?Molto, altrimenti non sarebbero “grosse” questioni, ma giochi o enigmi.
5. Quanto conta il formalismo?In alcuni casi utilizzarne uno adatto è indispensabile, e idearne uno nuovo costituisce un passo avanti. In altri casi non conta nulla.
6. Matematica e grammatica sono legate?La matematica ha una sua grammatica, come ogni linguaggio.
6b. Lei parla “matematica” correttamente?Ci provo, non sempre ci riesco.
7. Quanto bisogna essere portati per riuscire in matematica?È necessario ma non sufficiente (come direbbe un matematico); non tutti i grandi matematici sono stati dei bambini prodigio: la passione e la dedizione sono ugualmente necessarie.7a. Per fare cosa bisogna avere meno di trenta anni?Conosco matematici che hanno dato il loro meglio ben oltre i trent’anni. Però quando si è giovani si impara velocemente, con più entusiasmo; bisogna davvero approfittarne!
7b., Lei è portata? E da quando?Portata? Sì dalla determinazione. Fin da quando mi ricordo ho amato la matematica e mi ci sono dedicata molto, nei giochi da bambina e approfondendola per conto mio durante le scuole superiori. Non so se ho un particolare talento, ma una particolare passione direi proprio di sì.
***
FantamatematicaVite immaginarie, eventi improbabili, aneddoti completamente infondati, testimonianze palesemente contraddittorie, imbarazzanti documenti inediti di pura invenzione sconfessati da eredi, contemporanei e gente di buonsenso. Questo e altro nei racconti umoristici in salsa matematica curati da Stefano Pisani.
Isaac “Mad Dog” Newton – Parte ILa vita più o meno segreta di Isaac Newton, grandissimo matematico, fisico, filosofo naturale, astronomo, teologo ed alchimista inglese raccontata da documenti inediti, sottratti ingiustamente al vaglio della Storia semplicemente perché immaginari.Sir Isaac Newton nacque a WoolsthorpebyColsterworth il 25 dicembre 1642 e morì a Londra il 20 marzo 1727. Forse. Perché la data si riferisce al calendario Giuliano a quel tempo vigente in Inghilterra. Secondo il calendario Gregoriano, attualmente in vigore, Isaac Newton è nato invece il 4 gennaio 1643 e deceduto il 31 marzo 1727. Si racconta che quando Newton, in punto di morte, realizzò di non essere nato il 25 dicembre 1642 ma il 4 gennaio 1643, si alzò improvvisamente dal letto urlando: “non voglio morire! Sono ancora un ragazzino!”. Ma ormai la cattedrale di Westminster era prenotata. È stato un grandissimo matematico, fisico, filosofo naturale, astronomo, teologo ed alchimista inglese.Newton nacque dunque a WoolsthorpebyColsterworth (città famosa per essere un ottimo riempitivo negli articoli in cui non si sa cosa scrivere) in una famiglia di allevatori. Suo padre, anch’egli di nome Isaac, morì tre mesi prima della sua nascita, lasciandogli il nome tutto per sé. Tre anni dopo, sua madre Anna Ayscough si accorse della dipartita del marito e si risposò con un vicario, Barnabas Smith, di 64 anni, lasciando il piccolo Isaac alle cure dei nonni materni. In quegli anni egli fu molto infelice: odiava il suo patrigno e pare che una volta sia giunto a minacciare di incendiare la sua casa. Nel 1653, quando Isaac aveva dieci anni (o 441, secondo il calendario Klingon), il patrigno morì lasciandogli un'eredità non indifferente con cui poté pagarsi l'istruzione alla King's School, a Grantham, e cremare il padre personalmente.Alloggiava presso la famiglia Clark, imparentata con i Newton. In questo periodo, il ragazzo si fece una reputazione quale costruttore di aquiloni, lanterne, giocattoli, modelli funzionanti di piccoli mulini, lanciafiamme. La scuola di Grantham, dove la matematica era pressoché ignorata, interessò ben poco Isaac che sviluppò le sue qualità di autodidatta leggendo i libri ereditati dal patrigno e quelli del farmacista Clark. In particolare, fu affascinato dalle preparazioni del farmacista e qui nacque il suo duraturo interesse per la chimica. A Newton interessava soprattutto un prodotto chimico spesso esposto da Clark, la figliastra Catherine Storer. Con Catherine, Isaac ebbe l’unica relazione della sua vita. In vecchiaia, ripensando teneramente a quella storia, soleva ricordare: “Vista una, viste tutte”. Il ragazzo aveva un carattere spigoloso, chiuso e altezzoso. Non amava il contatto con gli estranei e spesso minacciava chiunque lo avvicinasse per salutarlo di bruciargli la casa.Alla fine del 1658, la madre lo costrinse a abbandonare gli studi e lo richiamò a casa per accudire i campi ma Newton si rivelò un pessimo agricoltore. Alla fine il suo maestro convinse sua madre a fargli proseguire gli studi al Trinity College di Cambridge dove si trasferì nel 1661. A quel tempo gli insegnamenti del College erano basati su Aristotele, ma Newton preferiva filosofi più moderni come Cartesio, Galileo, Niccolò Copernico e Keplero. Nel 1665, scoprì il teorema binomiale. Poco dopo il College fu chiuso per via della peste che si stava diffondendo nella zona partendo da Londra. Newton approfittò di essere finalmente solo per proseguire gli studi per conto suo. Durante questo periodo in cui la morte nelle benigne vesti della peste bubbonica gli portava via tutti quelli che lo circondavano, a soli 22 anni scoprì “il metodo di Newton” (meravigliandosi di non averlo scoperto prima, tanto più che portava anche il suo nome) e approssimò le serie armonica usando i logaritmi, dato che sottomano non si trovava nient’altro.Inoltre, iniziò a sviluppare il calcolo infinitesimale, che fu per lui motivo di grande orgoglio, dato che questa scoperta gli diede la possibilità di infliggere del dolore a Gottfried Leibniz. I due ebbero infatti una disputa sulla paternità del calcolo infinitesimale. Newton sviluppò il calcolo infinitesimale, ma rese pubblica la cosa con 10 anni di ritardo, sostenendo di non averlo fatto prima per timore di essere deriso. “Vedete – si legge in una sua memoria totalmente inventata – questo calcolo infinitesimale si fa coi numeri piccoli piccoli, che somigliano schiettamente ai miei mulini in miniatura. Non volevo che la gente prendesse i miei scritti, e dopo averli letti me li pigiasse su per le ampie froge, esattamente come avveniva per i mulini”. Fra Leibniz e Newton comincerà uno scontro violentissimo. In realtà la scoperta di Leibniz, risalente al 1674 ma resa nota
nel 1684 nel Nuovo metodo per la determinazione dei massimi e dei minimi, avvenne indipendentemente da quella di Newton. Leibniz, successivamente, inventerà inoltre una macchina calcolatrice capace di moltiplicare, dividere ed estrarre radici quadrate dalle orecchie di Newton.Nel 1699 alcuni membri della Royal Society accusarono Leibniz di plagio, e iniziò una durissima contesa su chi avesse inventato il calcolo. Questa disputa amareggiò le vite di entrambi i contendenti fino alla morte di Leibniz nel 1716. Anche dopo la sua morte Newton continuò a denigrare la memoria dell’avversario fino al punto che, secondo alcuni, sarebbe arrivato a compiacersi di avergli “spezzato il cuore”[1]. La questione rimase incerta per così tanto tempo che al biografo di Leibniz venne un esaurimento nervoso. In quegli anni, Newton diventò prete anglicano e cominciò ad occuparsi di ottica fino al 1672. Il suo impegno per la scienza è chiaramente dimostrato da un particolare esperimento sull’ottica. Avendo l'idea che il colore fosse provocato dalla pressione sull’occhio, egli premette un ago da cucito intorno al suo occhio fino a quando poté dare dei colpetti al retro dello stesso, notando “cerchi bianchi, scuri e colorati fintanto che continuo ad agitarlo. Vedete? Venite pure, colleghi scienziati, date anche voi dei colpetti: io vedrò tanti colori. Ve lo garantisco sto vedendo dei colori, credetemi. Dove siete tutti? Vedo solo il colore nero. Qualcuno prenda delle bende”. Il giorno dopo, Newton ricevette i complimenti di un circo e una proposta di lavoro che rifiutò perché non vedeva dove doveva firmare.Nel 1671 la Royal Society lo chiamò per una dimostrazione del suo telescopio riflettore. Newton comincio' a fare i suoi discorsi sulla luce bianca che si scompone e poi si ricompone e poi si scompone di nuovo e poi si ricompone e poi si scompone e poi si ricompone e quando Robert Hooke criticò alcune delle sue idee, Newton ne fu così offeso che si ritirò dal dibattito pubblico borbottando qualcosa sul fatto che avrebbe inventato come scomporre Hooke. I due rimasero nemici, ma solo fino a quando Hooke non perì nell’incendio della sua casa. Continua... [1] Nel 1708 il fisico Keill, difese vigorosamente Newton in un articolo su un giornale. Per via dell'insistenza di Leibniz la Royal Society nominò una commissione incaricata di studiare la questione. Sembra che Newton, nella sua carica di presidente, abbia influito sulla scelta della commissione. Ovviamente dunque questa diede ragione a Newton sostenendo la sua paternità dell'invenzione del calcolo e accusando Leibniz di plagio. Probabilmente Newton stesso redasse il rapporto finale senza firmarlo, ma era facilmente riconoscibile per tutti quei riferimenti insoliti alla virtù compromessa della sorella di Leibniz. Leibniz si scagliò allora violentemente contro Newton mettendo in discussione la paternità della teoria della gravitazione universale, la sua ortodossia religiosa e accusandolo di essere, in realtà, una monade con tre porte e due finestre. Newton rispose a tono e la disputa coinvolse la maggior parte dei matematici del tempo trasformandosi in un vero e proprio caso diplomatico che tra l'altro ostacolò la diffusione delle teorie newtoniane nel continente. Ancora nel 1726, dieci anni dopo la morte di Leibniz, Newton eliminò dai Principia ogni accenno al fatto che i due avessero sviluppato indipendentemente il calcolo infinitesimale. Oggi gli storici della scienza tendono a riconoscere a Newton una priorità nelle applicazioni fisicomeccaniche del calcolo, e a Leibniz una priorità sugli aspetti logicomatematici e sui trattini usati per le "t".
I luoghi della matematicaLa matematica è fatta anche di “luoghi”. Grazie ai nostri “inviati” speciali sul posto, conosciamo università, centri di ricerca, festival e altri luoghi e eventi in cui la matematica è protagonista.
[#15] EMS 2012: Un matematico al CongressoCamillo De Lellis è un matematico italiano molto noto per i suoi brillanti risultati, questa è la sua pagina web (perché stranamente non è la prima uscita che trovate digitando il suo nome su Google...). I lettori di Maddmaths! lo conoscono per un’intervista di qualche tempo fa. Questa volta si traveste da reporter e ci racconta il suo punto di vista sull’ultimo convegno europeo di matematica a Cracovia.
di Camillo de Lellis
È una giornata d’aprile, bella e tiepida per quanto consenta il clima della zona in cui vivo. Un’influenza mi impedisce il duro lavoro intellettuale che solitamente mi dà il pane, ma non resisto comunque al rito della posta elettronica. Nell’Inbox c’è un messaggio di Roberto, che mi propone di scrivere qualche pagina sul sesto European Congress of Mathematics per il sito di “MADDMATHS!”. Dovrei rifiutare, ma l’influenza mi ottunde e mi gioca un brutto scherzo. Più onestamente credo sia colpa del mio ego: il modello di Roberto “sarebbero i reportage di Wallace per Harpers magazine” e si rivolge a me perché sa che “sono un lettore” ed è “sicuro che scriva bene”. Qualche giorno dopo mi rendo conto che posso solo coprirmi di ridicolo, ma nei cinque mesi trascorsi dal congresso tutti i miei tentativi di svicolare sono andati a vuoto. Roberto non molla ed eccomi qui a scrivere il “reportage dall’interno” (parole di Roberto, come in tutti gli altri virgolettati di questo paragrafo).Il sesto congresso europeo di matematica si tiene i primi di luglio a Cracovia, dove atterro la domenica della finale degli europei dopo un volo piuttosto turbolento e uno tranquillo. Quando arrivo in albergo a fine serata non sta andando affatto bene per noi, ma resisto davanti al televisore della mia camera fino alla stanca e triste conclusione.La mattina della prima giornata iniziamo con la solita cerimonia di apertura dei congressi di queste dimensioni, che per fortuna questa volta è decisamente sobria. Le autorità si astengono dai tipici noiosi e triti discorsi, l’unico neo del cerinoniere è che non può astenersi dal ricordarci la Spagna fresca vincitrice degli Europei di Calcio. Ho paura che sia solo la prima di una lunga serie di simili osservazioni e invece no, il resto della settimana non mi riserva neanche un semplice sfottò, sembra che siano tutti troppo contenti che l’Italia abbia eliminato la Germania. Alla cerimonia d’apertura segue la consegna dei premi e tra i premiati ci sono Alessio Figalli e Corinna Ulcigrai, che conosco fin da quando erano ragazzi (Alessio avrà avuto 16 anni la prima volta che l’ho incontrato a uno dei corsi estivi delle Olimpiadi della Matematica). Non posso non sentire un certo orgoglio, visto che sono passati tutti e due da Pisa, come me. Devo proprio aggiungere che nessuno dei due è in Italia? La generosità del nostro paese è stupefacente: i tanti, ottimi, giovani scienziati che le nostre università formano con fatica li cediamo munificamente al resto del mondo.Il congresso si tiene in un palazzetto ultramoderno, la sala principale è fatta davvero bene e, nonostante le dimensioni, l’acustica è impeccabile. Nel programma molti contributi che vertono su temi analoghi sono previsti in contemporanea ed è troppo sistematico per non tradire una chiara intenzione degli organizzatori. Probabilmente vogliono incentivare i partecipanti a seguire anche conferenze di cui non sono esperti, ma l’impressione è che la strategia non abbia funzionato a dovere e alcune delle grandi aule sembrano, malinconicamente, un po’ vuote. Decido che nei prossimi giorni asseconderò gli organizzatori e salterò molte conferenze di chi conosco bene, per lasciarmi sorprendere da qualcuno che non conosco affatto. Quindi non andrò a sentire né Alessio né Benjamin Schlein, i due amici con cui dividerò la quasi totalità delle cene; ma in un caso me ne pento, perché la conferenza che scelgo non è all’altezza: è una classica “listadellaspesa”.Le conferenze che chiamo listedellaspesa consistono di un lungo elenco di svariati risultati, cosí fitto che lascia poco o nulla a commenti e idee. Anche se in alcuni casi possono dare un’utile panoramica su cosa sta succedendo in un certo settore, è improbabile che le listedellaspesa riscuotano piú di qualche sbadiglio davanti a una platea variegata. Sono però una tentazione a cui è difficile resistere e uno dei conferenzieri della prima giornata, un matematico esperto che, mi dicono, sa come coinvolgere la platea, ci cade in pieno.
Deve essere fuori forma perché oltre a risultare piuttosto noiosa e (credo) incomprensibile a chi non ha una certa familiarità con la materia, la sua lezione finisce per essere un compendio degli errori da evitare accuratamente, a partire dal più banale: un carattere troppo piccolo che dalla terza fila non si legge già piú.La prima giornata ha il suo acuto nella lezione di Simon Brendle. Non è una delle conferenze più belle che gli abbia sentito fare, ma si tratta comunque della soluzione di una famosa congettura di Lawson degli anni Settanta, sull’unicità del toro di Clifford quale superficie minima di genere uno embedded in S3. Simon è ormai abbonato a risultati di questo tipo. Curiosamente il 2012 è stato l’anno del toro di Clifford, con la soluzione di un’altra celebre congettura che lo riguarda, la congettura di Willmore. Probabilmente l’unica critica seria che posso muovere al congresso di Cracovia è che nessuno dei due brillanti solutori, André Neves e Fernando Codá Marques, è presente. Fernando è brasiliano e lavora all’IMPA di Rio, ma è difficile immaginare un’occasione migliore per invitare André, che è portoghese e professore all’Imperial college. A difesa degli organizzatori va detto che la soluzione della congettura è apparsa a marzo, quando probabilmente il programma del congresso era già stato deciso; tra l’altro è un malloppo di un centinaio di pagine. La soluzione di Simon della congettura di Lawson è, invece, sorprendentemente breve.Nel primo giorno ho subito occasione di farmi un’idea della città. Cracovia è effettivamente bella: lo si dice sempre, ma in questo caso è vero. Il centro storico lo è in modo convenzionale e purtroppo è parzialmente rovinato dal turismo di massa. Ogni sera, mentre cerchiamo un posto in cui cenare, ci vengono offerti biglietti per svariati strip club, corredati da commenti in italiano sulla bontà dell’intrattenimento (un tizio cita il BungaBunga, tristemente celebre anche qui); decido che è l’aspetto equivoco dei miei amici a catalizzare le offerte. Il resto della città ha cose meno convenzionali da offrire, in particolare quell’atmosfera da Europa orientale che non so ben definire, ma che si avvale anche del fascino dei piú deleteri prodotti architettonici del socialismo reale.Nel pomeriggio del secondo giorno mi trovo a seguire una delle lezioni più interessanti di tutto il convegno, tenuta da Martin Hairer, un probabilista austriaco che lavora a Warwick. Ho sentito parlare di Hairer in diverse occasioni con toni assolutamente lusinghieri e ho anche avuto l’opportunità di assistere a una sua lezione durante un convegno del SIAM. Non ero stato però particolarmente attento perché il mio intervento era subito dopo il suo. Questa volta non ho scuse e posso godermi tutta la conferenza; è l’esatto contrario di una listadellaspesa ed è incentrata su un suo risultato recente, che a un profano come me sembra basarsi su una serie impressionante di idee nuove e interessanti. Lo stesso pomeriggio mi riserva anche uno dei punti più bassi del convegno: un intervento a “parte interna vuota”. Il conferenziere decide di fare solo intrattenimento e forse ha ragione, visto che è la fine della giornata, ma dietro (almeno secondo me) non c’è il necessario supporto matematico. Allora preferisco la lista della spesa, se le voci sono della qualità necessaria.Il mercoledì è la giornata dei giganti, con tre conferenze per cui sarei tentato di usare l’aggettivo “epiche”, se non suonasse così stucchevolmente melodrammatico. La prima la tiene Talagrand, un celebre probabilista francese, uno di quei nomi che senti ripetere con reverenza in talmente tante occasioni che cominci a sospettare che non si tratti di una persona in carne e ossa. È la prima volta che lo vedo e ho deciso di andare a sentirlo nonostante le voci poco incoraggianti (riassumendo l’opinione di alcuni amici, non si capirà un accidenti): nella peggiore delle ipotesi conto di poter associare una faccia a un nome. La sua presentazione è invece bellissima: chiara, coinvolgente, con la giusta dose di humour. Francamente mi sarei sentito fuori posto a parlare dopo Talagrand e non invidio Cristopher.Anche se il nome Cristopher Hacon non lo lascia sospettare, il secondo conferenziere è un nostro connazionale e, nonostante i tanti anni trascorsi all’estero, nel suo italiano si sente ancora un inequivocabile accento pisano. Anche lui è passato da Pisa, anche lui non è in Italia, perché ha lasciato il paese subito dopo la laurea e si è dottorato negli Stati Uniti. Da studente conoscevo molto bene suo fratello, che ha studiato fisica (“ah, ma è quello che assomiglia a Kurt Cobain” è il commento di un’amica a cui tentavo di far capire chi fosse Johnny Hacon). Cristopher smentisce il credo di tanti matematici: è inutile andare a una conferenza di geometria algebrica se non sei un geometra algebrico, perché non capirai neanche di cosa si sta parlando. Onestamente Cristopher non è accattivante come Talagrand, che ha potuto contare su problematiche indubbiamente piú intuitive e semplici da formulare. Però fa una bella lezione, accessibile a chiunque abbia un’infarinatura decente, anche se un po’ arrugginita, su un argomento che ha l’indubbio fascino dei classici: la classificazione della varietà algebriche. Si sente un grande respiro; mi sembra che Cristopher sia entrato nella storia della matematica, con dei teoremi che saranno ancora lí tra anni e anni. È l’impressione di un profano, ma non credo di sbagliarmi. Mi consolo pensando che comunque lui non assomiglia affatto a Kurt Cobain, tutto sommato c’è un po’ di giustizia in questo mondo.
Se sono un profano nelle materie delle due conferenze appena citate, per la terza non è così. Dai primi anni del dottorato fino ad oggi ho sudato per parecchie ore sugli scritti di Vladimir Šverak e non me ne sono mai pentito: una discreta parte dei miei lavori piú apprezzati ne sentono l’influenza. Vladimir si è occupato di alcune questioni fondamentali del calcolo delle variazioni e sulle equazioni alle derivate parziali, per la maggior parte motivate da famosi problemi della fisica matematica. Molti dei suoi lavori contengono, ad oggi, i risultati piú significativi e profondi nel corrispettivo ambito di ricerca, ogni volta raggiunti grazie a un punto di vista nuovo, a una connessione inaspettata tra gli argomenti piú disparati. L’originalità delle sue idee colpisce anche nei primissimi articoli che ha scritto e ho perso il conto delle volte in cui mi sono chiesto “ma come diavolo gli è venuto in mente”? E come tante idee profonde della matematica, i punti di vista innovativi di Vladimir diventano, dopo un po’, quelli piú “naturali”. Così mercoledì pomeriggio ho violato la mia promessa di sacrificare il noto (a me) a favore dell’ignoto. Ne è valsa la pena perché Vladimir, come al solito, ha fatto una conferenza ispirata: manco a dirlo, un nuovo punto di vista su un problema classico.Il giovedì nella prima mattinata il congresso tocca il fondo, è il mio turno. A parte Maria, la mia chairman, che al primo secondo fuori tempo massimo mi toglierà la parola, non ho altri motivi per preoccuparmi perché nella platea mancano i due che potrebbero smentirmi. Uno è László Székelyhidi, il compagno di battaglie con cui ho scritto tutti i miei lavori che menzionerò oggi. Alla fine del 2006 ci siamo accorti di una cosa curiosa: alcuni “mostri” della letteratura delle equazioni differenziali alle derivate parziali, che fino ad allora occupavano un posto particolare, si possono spiegare in modo semplice ed elegante con l’hprincipio, un concetto introdotto da Gromov per riunire alcuni tra i piú sconcertanti fenomeni della geometria differenziale, come il “paradosso” di NashKuiper. La sorpresa sta nel fatto che i mostri sono soluzioni delle equazioni di Eulero, un classico sistema della fluidodinamica incomprimibile. Cito Gromov piú volte, in particolare una sua frase sull’improbabilità che l’hprincipio si possa applicare a delle equazioni della fisica matematica, cosa che io e László siamo orgogliosi di aver smentito. È un po’ azzardato, perché stiamo parlando di un commento forse marginale, ma fortunatamente Gromov, anche lui assente, non può intervenire.Quella che all’inizio del 2007 sembrava una curiosa, seppur intelligente, osservazione, negli ultimi 5 anni si è evoluta in un ambizioso progetto di ricerca. Dopo esserci imbattuti in molte altre coincidenze, alla fine del 2007 abbiamo proposto, come possibile applicazione dell’hprincipio, una linea di attacco a una congettura del 1949 avanzata da Lars Onsager in un suo celebre lavoro sulla teoria della turbolenza. La congettura afferma l’esistenza di soluzioni delle equazioni di Eulero che dissipano l’energia cinetica ma che sono continue, con esponente di Hölder minore di 1/3. Dopo quattro anni di duro lavoro siamo finalmente riusciti a dimostrare che soluzioni continue dissipative effettivamente esistono e all’inizio di maggio abbiamo anche raggiunto la regolarità Hölder: il nostro esponente per ora è 1/10, un numero di tutto rispetto come primo tentativo (a novembre un brillante dottorando di Princeton ha migliorato nella sua tesi i nostri metodi spostando la soglia a 1/15).Spero di non aver fatto una lista della spesa. Mi premerebbe convincere la comunità che i nostri risultati non sono cosí strani come sembrano a prima vista, ma che anzi presentano “indizi” sulla correttezza di molte considerazioni dei fisici sulla teoria della turbolenza, anche da un rigoroso punto di vista matematico e non solo da quello fenomenologico. Il problema è che i nostri risultati sono difficili da inquadrare nell’ottica della classica letteratura sulle equazioni alle derivate parziali. Il verbo imperante è “mostrare la buona positura” e i nostri fanno tutto il contrario: otteniamo tante, troppe soluzioni. Inoltre l’analista classico vuole le “stime hard” e fino a qualche anno fa le stime dei nostri lavori erano troppo “soft”; il vero duro è quello che ha la stima piú lunga. Almeno questo aspetto frivolo è migliorato negli ultimi due lavori sulle soluzioni continue: nessuno che abbia gettato uno sguardo serio agli ultimi scritti può contestarci la presenza di decine di stime lunghe e complicate.La giornata di giovedí è stata piuttosto pesante e la stanchezza si fa sentire ancor di piú durante l’ultimo giorno: tengo fede al proposito di evitare le conferenze piú vicine ai miei temi di ricerca, ma non ne ricavo granché. Come mi è successo molte altre volte, la mia speranza di vedere Gromov è rimasta delusa: avrebbe dovuto chiudere il congresso ma ha poi cancellato il suo intervento per motivi di salute. Al pomeriggio decido di saltare la cerimonia di chiusura per fare una visita all’ex fabbrica di Oskar Schindler...Bisogna pur concedere qualcosa al turismo di massa prima di tornare a casa.
L’Alfabeto della MatematicaLa matematica... in ordine alfabetico. A come Approssimazione, B come Brachiostocrona, C come convessità... ogni mese un concetto matematico spiegato con semplicità e in modo coinvolgente da Corrado Mascia.
T come Trasformata
Anche la matematica permette di compiere piccole magie. Un colpo di penna, qualche formula magica, e una carta di cuori diventa di picche. Illusionismo? No, trasformismo... Il principio non è particolarmente esotico: si tratta di vedere lo stesso oggetto sotto un punto di vista diverso che, se ben scelto, può rivelare proprietà altrimenti nascoste.Partiamo da un esempio geometrico: un insieme convesso, cioè uno che contiene tutti i segmenti che congiungono i punti dell'insieme. Un cerchio, un ellissi, un quadrato... fate voi. In genere, un insieme del piano si individua descrivendo il bordo che lo contiene, come nel caso di un cerchio che è individuato dalla circonferenza che lo delimita. Per un convesso, esistono maniere alternative, magari meno naturali, che definiscono l'insieme altrettanto bene. Ad esempio, un insieme convesso si può rappresentare come intersezione di semipiani e per la precisione come intersezione di tutti i semipiani delimitati da rette tangenti al suo perimetro. Folle? No, ...visionario! Perché questa visione permette, a volte, di riconoscere simmetrie nascoste. Questa maniera anomala di individuare insiemi convessi è il cuore (geometrico) della “trasformata di Legendre” che in meccanica permette il passaggio dalla formulazione lagrangiana a quella hamiltoniana ed in termodinamica costituisce il legame tra energia ed entalpia, transizioni attraverso cui capita che il misterioso disordine delle strutture si trasformi in formule ordinatamente sintetiche.Quella di Legendre è una delle tante trasformate che scorrazzano nei corridoi dei dipartimenti di Matematica e non solo. La regina di tutte è sicuramente la trasformata di FourierLaplace (si tratta in realtà di due procedimenti leggermente diversi tra loro che prendono l'avvio dallo stesso principio). Alla base ci sono due idee cruciali. La prima consiste nel fatto che un segnale (ad esempio, il suono congiunto di una orchestra) può essere rappresentato come sovrapposizione di segnali elementari che, nel caso della trasformata in questione, sono dati da esponenziali (reali o complessi). Conoscere il peso di ciascuno degli oggetti elementari equivale a conoscere il segnale completo. Quindi, dall'informazione relativa al quantitativo di ogni singolo ingrediente presente, si ricostruisce la miscela. A questo livello, si tratta sempre di “preparazioni lineari”, cioè ricette in cui la somma degli elementi descrive il piatto completo, per via dell'assenza di interazioni anomale (che diremmo nonlineari) tra le parti...La trasformata di FourierLaplace possiede un potere magico aggiuntivo e, per gli esperti, strabiliante: tramutare l'operazione di derivazione in quella di moltiplicazione (grazie alla scelta esponenziale). La conseguenza notevole è che equazioni differenziali lineari, che altro non sono se non relazioni tra derivate di una funzione incognita, vengono di colpo trasformate in relazioni algebriche. Risolvere una equazione differenziale del primo ordine diventa facile come trovare le soluzioni di una equazione di primo grado, cioè trovare le intersezioni tra rette.Equazioni di secondo grado si traducono in polinomi di secondo grado, per cui occorre fare appello a parabole e formule risolutive più o meno note. Con un colpo di bacchetta, si passa dal linguaggio differenziale a quello dell'algebra con il pregio di trovarsi a poter adoperare i potenti mezzi di una disciplina che, prima della trasformazione, sembrava solo un mondo distante.Capita poi che i conti vadano fatti sul serio e tanta elegante teoria matematica non sempre sia sufficiente. La trasformata di Fourier è un oggetto che vive in spazi di dimensione infinita e la cosa non va d'accordo con la nostra disponibilità limitata di tempo... Senza darsi per vinti, si possono introdurre versioni “leggere” della stessa operazione, come la trasformata di Fourier discreta che, attraverso l'uso dei computer e della loro potenza di calcolo, permette di calcolare, in concreto, il valore numerico degli ingredienti in gioco. E, visto che c'è sempre qualcuno che non si accontenta, si possono anche proporre versioni più efficienti per il calcolo e considerare quella che è stata definita “il più importante algoritmo numerico del nostro tempo”, la cosiddetta “Fast Fourier Transform”, o trasformata di Fourier veloce, buona per tutti quelli che vanno veramente di fretta.
Fantamatematica
Gauss il genio timidoVita di Gauss, il genio timido che morì per un attacco di perfezionismo.di Stefano Pisani
Johann Carl Friedrich Gauss (Braunschweig, 30 aprile 1777 – Gottinga, 23 febbraio 1855) è stato un matematico, astronomo e fisico tedesco che ha dato contributi determinanti in vari campi, inclusi analisi matematica, statistica, calcolo numerico, geometria differenziale, geodesia, geofisica, magnetismo,
elettrostatica, astronomia, ottica, teoria dei numeri in salsa tartara e ingegneria del pinnacolo.Secondo la leggenda, all’età di tre anni il piccolo Gauss avrebbe corretto un errore del padre nel calcolo delle sue finanze. Si racconta che il padre rimase molto stupito, soprattutto per il fatto che, fin quando Johann Carl Friedrich non glielo aveva fatto notare, non si era accorto di avere un figlio. Un altro aneddoto racconta che a nove anni di età, quando andava a scuola, il suo insegnante, J.G. Büttner, per mettere a tacere i turbolenti allievi, ordinò loro di fare la somma di tutti i numeri da 1 a 100. Pochi secondi dopo, il giovanissimo Johann Carl Friedrich diede la risposta esatta. L’insegnante fu talmente sorpreso che diede in escandescenze e i ragazzi, per
calmarlo, dovettero dargli delle cifre da sommare. I dettagli della storia sono però assai incerti: qualcuno ritiene che Gauss si sia accorto che, mettendo in una riga tutti i numeri da 1 a 100 e nella riga sottostante i numeri da 100 a 1, ogni colonna dava come somma 101. Fatto questo, chiese all’assistente dell’insegnante la soluzione. Recenti studi ipotizzano però che Gauss quel giorno fosse assente a causa degli orecchioni.Il 1796 fu probabilmente l’anno più produttivo di Gauss. Riuscì a costruire un eptadecagono, inventò l’aritmetica modulare e scoprì, inoltre, che tutti i numeri naturali sono rappresentabili al più come somma di tre numeri triangolari. Tuttavia Gauss non pubblicò questa scoperta ma la tenne per sé. Il matematico era infatti affetto da mania di perfezionismo che gli impediva di pubblicare le sue dimostrazioni se non erano assolutamente rigorose. Scriveva invece le sue scoperte nel suo diario in maniera criptica. Lo storico matematico Eric Bell stima che, se Gauss avesse pubblicato per tempo tutte le sue scoperte, avrebbe anticipato i matematici di almeno cinquant’anni. Ma stimò anche che quelli venuti dopo di lui avrebbero riportato indietro la matematica di cinquant’anni, quindi siamo in pari.Nel 1799 l’astronomo italiano Giuseppe Piazzi scoprì l’asteroide Cerere, ma lo poté seguire solo per alcuni giorni perché scomparve dietro la Luna. «Cos’è che avresti scoperto? Io non vedo niente» lo canzonavano i colleghi tedeschi «il solito italiano contaballe». Gauss, che era nascosto dietro una tenda arabescata, calcolò
il punto esatto in cui il corpo celeste sarebbe riapparso. Cerere, dopo qualche mese, fece capolino proprio nel punto indicato da Gauss. Per la sua mania di perfezionismo, però, Gauss aveva tenuto per sé la sua previsione e quando si presentò da Piazzi rivendicando il suo successo questi gli ruppe un astrolabio sul naso, invitandolo a prevedere da quale porta lo avrebbe cacciato.Nello stesso anno, Gauss dimostrò anche il Teorema fondamentale dell’Algebra[1], secondo cui ogni funzione algebrica integrale di una variabile può essere risolta in fattori di primo o secondo grado allineando fiammiferi. Gauss era un prodigioso “calcolatore mentale”. Si dice che si divertisse a setacciare un intervallo di mille numeri in cerca di numeri primi appena aveva un po’ di tempo libero. Era anche un lavoratore instancabile. Secondo Isaac Asimov, una volta, mentre stava lavorando ad un problema, sarebbe stato interrotto per riferirgli che sua moglie stava morendo. Gauss avrebbe risposto: «Ditele di aspettare un attimo, sono impegnato». Di fronte all’insistenza del medico, Gauss replicò: «Va bene, vi seguo. Ma mentre veglio il corpo
calcolerò numeri primi».
Una delle figlie di Gauss, che ebbe dal suo primo matrimonio con un trapezio isoscelePare che Gauss sia stato il primo a scoprire le potenzialità della geometria non euclidea, ma sembra che, per paura di pubblicare un lavoro così rivoluzionario, tenne per sé i risultati. János Bolyai invece scoprì ufficialmente la geometria non euclidea nel 1829, pubblicando poi il suo risultato nel 1832. Dopo averlo letto, Gauss scrisse a Farkas Bolyai, padre di Janos e suo amico fraterno che gli aveva chiesto un parere: «Lodare questo lavoro sarebbe come lodare me stesso. Infatti esso coincide quasi esattamente con le meditazioni che ho fatto trenta, trentacinque anni fa». «Trentacinque anni fa. Un periodo d’oro – gli risposte Farkas – dato che non ti conoscevo»Nel 1818 fu chiesto a Gauss di compiere una rilevazione geodetica dello stato dell’Hannover, associandola ai precedenti rilevamenti in Danimarca. Gauss accettò il compito di buon grado, applicandovi la sua straordinaria abilità nel calcolare. La cartografia dell'Hannover portò Gauss a sviluppare la distribuzione gaussiana degli errori, usata per descrivere la misura degli errori del cartografo che l’aveva preceduto. Sebbene avesse avuto alcuni studenti, Gauss era risaputo detestare l’insegnamento. Si dice che egli prese parte ad un’unica conferenza scientifica, che si tenne a Berlino nel 1828 e a cui intervenne travestito da logaritmo di 743.Johann Carl Friedrich morì a Göttinga nel 1855 e fu interrato nel cimitero di Albanifriedhof con il suo pallottoliere preferito. Chiese che sulla sua tomba fosse inciso un eptadecagono (un poligono con 17 lati) ma lo scalpellino rifiutò dicendo che esso non sarebbe stato distinguibile da un cerchio. Soprattutto perché lui sapeva fare solo cerchi. Stefano Pisani
[1] Prima di lui, altri matematici, incluso Jean Baptiste Le Rond d'Alembert, avevano proposto delle false dimostrazioni del teorema al puro scopo di seminare zizzania.
Focus
La matematica delle impronte digitali
di Riccardo Aragona, Massimiliano Sala e Claudia Tinnirello
Agenti segreti che entrano in aree protette facendosi riconoscere attraverso la propria iride, persone che vengono identificate dal computer semplicemente premendo il proprio pollice sullo schermo: non si tratta di sceneggiature futuristiche o romanzi di fantascienza, ma di una realtà sempre più vicina.
Negli ultimi anni si è sviluppato un campo di ricerca scientifica,la biometria, che si occupa dell'identificazione di persone attraverso sistemi che si basano su caratteristiche fisiologiche / comportamentali (come appunto l'impronta, l'iride, la grafia e la voce). Ormai le applicazioni sono moltissime e spaziano dal controllo di accessi in aree protette, passando per aspetti legati alla firma di contratti, fino ad arrivare ai pagamenti online. Si tratta di un campo in continuo sviluppo ed espansione. L’applicazione più promettente è la sostituzione completa di metodi scomodi per “condividere i segreti”, quali le lettere che arrivano a casa contenenti password o PIN oppure i dispositivi, detti token, che generano successioni di numeri da inserire nei siti.
Vi sarà sicuramente capitato di scegliere una password, formata da lettere, numeri e simboli, per sbloccare il vostro cellulare o il vostro computer. Immaginate ora di possedere un touchscreen (beh, magari lo possedete già!) e di voler fare in modo che solo voi possiate accedervi. Potreste scegliere una password alfanumerica, come la precedente, o potreste scegliere un segno grafico (ad esempio una stella, un cerchio o magari la vostra firma) da tracciare sullo schermo con le vostre dita. Ma come può il computer sapere che siete il suo "padrone"? Se qualche estraneo avesse visto, o indovinasse, la figura che disegnate sullo schermo per accedere, e provasse a ripeterla, come potrebbe il computer sventare l’assalto ai vostri dati? Sfruttare caratteristiche fisiologiche ed usare la biometria, potrebbe essere una buona soluzione. Tracciare un disegno (che di fatto sarà la vostra firma) sullo schermo è come mandare un messaggio al computer. Piccole variazioni della firma provocano piccole variazioni nel messaggio, che quindi sarà simile al primo, ma non identico. Come fa il computer a capire che i due messaggi corrispondono alla stessa persona, ovvero al suo legittimo proprietario? È qui che entra in gioco la matematica, in particolare la teoria dei codici a correzione di errore.
La teoria dei codici è una branca della matematica che si occupa dello studio e della correzione di errori nella trasmissione di dati. Il primo ad occuparsi da un punto di vista matematico di trasmissione di dati e possibili interferenze fu Claude Elwood Shannon nel 1948, in un suo brillante articolo rimasto nella storia [1].
Vi sarà senz'altro capitato di parlare con un vostro amico che si trova piuttosto lontano da voi, mentre siete all’aperto (ad esempio durante una camminata in montagna). Vi sarete sicuramente accorti che non vi arrivava perfettamente quello che il vostro amico cercava di dirvi, magari vi arrivavano parti di frasi oppure, ancora peggio, parole troncate; in qualche modo, frasi e parole errate. Voi, per cercare di capire tutto il discorso, avrete tentato di interpretarlo; avrete dunque provato a modificare le frasi incomplete e le parole troncate per ottenere frasi e parole di senso compiuto. Se la vostra interpretazione è giusta, la modifica da voi fatta si chiama “correzione”. Senza saperlo, avete utilizzato la teoria dei codici.
In generale il processo di comunicazione dei dati si compone di tre oggetti: una sorgente (la persona o il dispositivo che invia i dati), un canale (il mezzo attraverso cui vengono trasmessi i dati) e un ricevitore (persona o dispositivo a cui i dati sono inviati). La trasmissione è soggetta a disturbi o interferenze presenti nel canale. Shannon mostrò come sia possibile trasformare l’informazione da inviare (codificare) in maniera tale che il ricevente possa ricostruirla esattamente (decodificare) nonostante i disturbi presenti nel canale (rumore).
Shannon infine dimostrò in modo rigoroso che la probabilità di decodifica sbagliata può essere resa arbitrariamente piccola.
Cerchiamo di fare degli esempi più tecnologici. Sotto i binari dei treni esistono dei dispositivi, dettibalise, che regolano il buon andamento dei treni. Il balise trasmette ordini al treno (ad esempio "aumenta la velocità", "fermati") utilizzando messaggi codificati che il treno decodifica. In assenza di codifica, gli errori di comunicazione provocherebbero danni, deragliamenti compresi. Un altro esempio in cui viene utilizzata la teoria dei codici è nei compact disc. La musica è trascritta su un CD come una sequenza di "0" e "1" (ovvero una sequenza binaria). I dati vengono scritti sulla facciata inferiore del CD tramite una serie di microscopiche incisioni. Il laser del lettore CD, scorrendo lungo la superficie del CD, legge "1" tutte le volte che rileva una variazione di profondità e "0" altrimenti. La sequenza binaria riproduce la musica originale.
Che cosa succede se graffiate la parte inferiore del CD? Ogni graffio aggiunge un'incisione che prima non c'era, cambiando ad esempio alcuni "0" in "1". Questo provoca un'alterazione della musica riprodotta dal CD, ovvero un "errore" di trasmissione. Fortunatamente la codifica applicata protegge la musica: non ci si limita ad inviare il messaggio binario, ma anche alcune informazioni aggiuntive. Queste hanno la funzione di proteggere i dati, in modo che il messaggio possa essere ricostruito in maniera esatta dal ricevitore nonostante l’informazione sia parzialmente compromessa. Questo espediente ha dei costi: nel caso dei CD, addirittura due terzi dello spazio sono utilizzati per riportare queste informazioni aggiuntive! Senza dati di protezione potremmo scrivere il triplo della musica, ma non riusciremmo a riprodurla esattamente.
Torniamo alla biometria. Come potrebbe funzionare un sistema biometrico di autenticazione? Qui le cose si complicano. Vediamone una versione semplificata, dando un'idea di come la teoria dei codici viene utilizzata nei sistemi di autenticazione.
REGISTRAZIONE
Supponete di aver deciso il disegno che vi identifica. La prima cosa da fare è comunicarlo al computer. Questa fase è chiamata registrazione. A differenza della password, un gesto non viene mai riprodotto due volte allo stesso modo e può subire delle variazioni che possono dipendere dallo stato emotivo dell'utente o semplicemente dalla posizione del braccio rispetto allo schermo. Questo è il motivo per cui il computer, in questa fase, vi chiederà di tracciare più volte (per esempio cinque volte) il disegno scelto. A questo punto, il computer estrae da ogni ripetizione del gesto alcune caratteristiche elementari: le coordinate spaziali (x,y), la pressione, la dimensione dell'impronta e un numero che cambia ogni volta che staccate il dito dallo schermo. Da questi pochi dati si possono ricavare molte caratteristiche del gesto, come la velocità media e l'accelerazione. Queste informazioni vengono opportunamente trasformate in una sequenza binaria. Dunque ad ognuna delle cinque ripetizioni del gesto verrà associata una sola sequenza di bit.
In teoria basterebbe conservare un'unica sequenza, che rappresenti "al meglio" le cinque ottenute in precedenza. Ma se vogliamo essere sicuri che nessuno possa ricostruire tali informazioni, pur intercettando uno dei canali di trasmissione o la memoria (database) in cui conserviamo la sequenza, occorre adottare qualche cautela in più. Vediamo come. Ricaviamo ancora un'unica sequenza che rappresenti "al meglio" le cinque firme, ma anziché conservarla, la combiniamo con una sequenza random di bit, che è stata precedentemente codificata, ottenendo una sequenza cifrata. Dalle cinque firme ricaviamo inoltre un numero, che chiamiamo il peso dell’errore, che indica quanto le cinque firme sono diverse l'una dall'altra. Conserviamo infine in un database: il peso dell'errore, la sequenza cifrata e un hash della sequenza random. Una funzione hash ha la proprietà che se cambia leggermente l’input allora cambia drasticamente l’output.
AUTENTICAZIONE
Ogni volta che proverete ad autenticarvi il vostro gesto verrà trasformato in una sequenza binaria. Essa verrà combinata alla sequenza cifrata, in modo "inverso" a come veniva fatto in fase di registrazione, e la sequenza così ottenuta viene decodificata usando il peso dell’errore. Si applica quindi alla sequenza binaria così ottenuta la funzione hash e il sistema confronta il risultato con il terzo dato conservato, cioè la versione hash della sequenza random. Solo se le due sequenze sono uguali, potrete accedere al computer.
[1] C. E. Shannon, "A Mathematical Theory of Communication", Bell System Technical Journal, vol. 27,pp. 379423, 623656, July, October, 1948.http://cm.belllabs.com/cm/ms/what/shannonday/shannon1948.pdf
Giovani Matematici crescono
Massimiliano Gubinelli e le equazioni alle derivate parziali con rumori molto singolari…
Massimo Gubinelli (1974) si è laureato in fisica e nel 2003 ha ottenuto il dottorato in fisica teorica a Pisa. Durante il periodo del dottorato si avvicina a un gruppo di matematici che studiavano problemi che lo appassionavano. Da questa frequentazione nascono diverse collaborazioni che hanno progressivamente spostato i suoi interessi di ricerca dalla fisica teorica a problemi più strettamente matematici. È stato nominato per cinque anni Membro Junior dell'Istituto Universitario Francese, onorificenza che spetta solo a otto matematici sotto i 40 anni che lavorano in Francia. Intervista raccolta da Maya Briani.
Sei laureato in fisica, come ti sei avvicinato alla matematica?In realtà ho fatto anche un dottorato in fisica teorica, a Pisa. Durante il periodo del dottorato mi sono avvicinato a un gruppo di matematici che stavano studiando problemi che mi appassionavano. Si trattava di descrivere il comportamento statistico dei fluidi turbolenti attraverso delle strutture geometriche coerenti, insomma immaginare che la complessità del movimento di un fluido molto caotico potesse essere spiegata come un collage di strutture molto ordinate ma disposte in maniera casuale, tipo vortici o simili. Dalla frequentazione di quel gruppo sono nate delle collaborazioni che hanno progressivamente spostato i miei interessi di ricerca dalla fisica teorica a problemi più strettamente matematici. In realtà i due campi di studio sono molto vicini e a voler essere onesti non esiste una suddivisione molto netta tra una ricerca seria in fisica teorica e una in matematica. Diciamo che è l'accento messo più sui modelli o più sugli strumenti per studiarli che, dal mio punto di vista, fa un po' la differenza tra fare della fisica teorica e fare della matematica (o della fisica matematica).
Qual è il tuo campo di studi?In questi ultimi anni mi sono occupato delle interazioni tra analisi e probabilità. Per esempio lo studio delle equazioni differenziali o alle derivate parziali in presenza di rumore o di segnali molto irregolari, per i quali gli approcci standard dell'analisi non funzionano molto bene e per i quali vengono alla luce fenomeni inaspettati. Più recentemente mi sono anche interessato a quello che succede quando il rumore facilita la dimostrazione di certi teoremi sulle equazioni differenziali, invece di renderli più complicati. Questo succede perché il rumore perturba l'evoluzione del sistema descritto dall'equazione in modo tale da renderla meno soggetta alle sue singolarità intrinseche. Insomma "sfuoca" un po' la situazione che quindi sembra più regolare di quello che ci si aspetta. Questi comportamenti sono controintuitivi (almeno per un intuito analitico) e quindi è sempre abbastanza divertente metterli alla luce, e soprattutto richiede spesso un punto di vista originale sul problema.
Qual è il risultato che ti ha dato più soddisfazioni finora?Nessuno. I risultati finiti di solito non mi danno molta soddisfazione. Mi appassiona cercare di capire un problema e sopratutto farlo in maniera semplice o legarlo in maniera inaspettata ad altri problemi. Insomma, passeggiare nel paesaggio matematico. Capita che quando arrivi da qualche parte la cosa più interessante, il viaggio che ti ci a portato, sia già finita. Allora guardi intorno per cercare di ripartire in una nuova direzione. Mi piace pure viaggiare leggero, che nel contesto vuol dire cercare di usare sempre strumenti abbastanza semplici disponibili nel campo di ricerca in cui mi sto muovendo. Di solito ci sono in giro persone molto più brave di me a rendere dei risultati nella loro piena generalità. Io cerco di descrivere quello che trovo nel caso più semplice per evitare che i dettagli tecnici oscurino il cuore del risultato.
C'è un risultato scientifico a cui stai puntando, in questo momento?Sì, ultimamente con alcuni colleghi e amici e un paio di miei studenti stiamo lavorando a una teoria abbastanza entusiasmante per studiare delle equazioni alle derivate parziali con dei rumori molto singolari. Equazioni che fino a poco tempo fa non si sapeva come gestire e che venivano scritte in modo formale o in modo approssimato. Abbiamo un quadro più chiaro di quello che bisogna fare e del senso da dare a queste
equazioni. Si tratta di capire in che modo le caratteristiche microscopiche dei modelli che queste equazioni descrivono abbiano degli effetti macroscopici e come descrivere questi effetti nel modo più efficace. Ci sono ancora molti problemi da risolvere ma si intravede l'inizio di un percorso promettente e questa è la situazione che preferisco, quella in cui si sta svegli fino a tardi per esplorare un'idea, pieni d'entusiasmo.
Come sei finito a Parigi?Per ragioni familiari, in realtà. Sono stato sposato con una parigina e abbiamo due bimbi piccoli. Vivere a Parigi ci è sembrata la cosa più semplice da fare nel momento in cui si doveva decidere se stabilirsi in Italia o in Francia. I francesi mi hanno ben accolto e sono riuscito a trovare subito un posto all'Università, prima a Paris Sud e ora a Paris Dauphine, università in cui lavoro dal 2008. Parigi è un luogo ideale per fare matematica ma qualche volta mi manca l'atmosfera di Pisa, la città in cui ho studiato, che resta a mio avviso un ottimo compromesso tra vitalità scientifica e qualità della vita.
Quali sono i tuoi “dream problems”?Piuttosto che dream problems io ho campi di ricerca che mi piacerebbe poter approfondire, se ne avessi il tempo e l'energia. Il sogno insomma è piuttosto lo spazio e le risorse che si vorrebbero avere. Mi piacerebbe per esempio capire meglio la geometria noncommutativa di Alain Connes o i lavori di un logico matematico che reputo molto interessante e che si chiama JeanYves Girard. Magari un giorno troverò un pretesto per far diventare queste mie curiosità parte della mia attività di ricerca vera e propria. Ma per ora mi limito a lavorare sulle due o tre cose in cui riesco meglio.
A parte la matematica, come passi il tempo? Cosa fai quando non fai matematica?Da quando ci sono i bimbi ogni istante che non dedico a loro o all'attività di insegnamento cerco di raggranellarlo per fare della ricerca e riempire quaderni di calcoli ragionevoli (di solito poco). Una passione a cui dedico molto tempo ma in maniera discontinua è la programmazione. Collaboro per esempio allo sviluppo di un software per scrivere dei documenti tecnici (e in particolare dei bei testi matematici) che si chiama TeXmacs (www.texmacs.org). Ovviamente ne parlo nella speranza di fare un po' di pubblicità subliminale. Programmare e in generale praticare e studiare i linguaggi di programmazione mi appassiona molto (per esempio linguaggi come Haskell o Coq). Quando un conto non torna lascio perdere e vado a nuotare oppure me ne vado in giro per Parigi a passeggiare. La città è piena di percorsi inaspettati e mi piace perdermi nella folla.
Cédrat Villani (Cédric Villani visto da Leo Ortolani)
Sulle tracce del mostroRecensione di “Un genio nello scantinato” di Alexander Masters (Adelphi 2013, trad. di Andrew Tanzi), la strana biografia di uno strano talento matematico. di Roberto Natalini
Come funziona una TAC? Semplificando molto, si fissa una retta che passa attraverso un corpo che si vuole esaminare e si fa partire in quella direzione un fascio di raggi X, e poi si misura la loro intensità dopo l'attraversamento, che è attenuata in modo esplicitamente correlato con la densità totale dei tessuti attraversati. Si ripete questa operazione per un numero molto grande di direzioni diverse. Esiste allora un oggetto matematico, chiamato trasformata di Radon inversa, che permette di calcolare la distribuzione interna della densità del corpo a partire dall'insieme totale dei valori misurati di intensità. Insomma, possiamo “vedere” qualcosa di inaccessibile e invisibile, a partire da tante misurazioni esterne e indirette. Forse non è poi così tanto sorprendente, ma non è facile e spesso si commettono errori. Però, pensandoci un po' meglio, a me sembra che quasi tutto nella nostra vita si svolga seguendo questa modalità. Se vogliamo conoscere una cosa qualsiasi, persona o particella subatomica, dobbiamo interagire con essa, farle emettere segnali, e poi unire i puntini, tanti o pochi che siano, cercando di capire cosa c'è dietro. Quando parliamo con qualcuno o guidiamo la macchina, elaboriamo continuamente segnali che ci permettono di ricostruire le intenzioni degli altri, esseri nascosti di cui captiamo solo le manifestazioni più esteriori. È come seguire le tracce di un animale nel bosco, non è facile e spesso si commettono errori. E ci sono due attività che sono particolarmente, se non esclusivamente, segnate da questa modalità di ricostruzione indiretta, e sono la matematica e la letteratura.In cosa consiste l'attività di un matematico? Spesso cerca solo di rendere visibile qualche cosa di altrimenti inaccessibile, di renderlo conosciuto e familiare. La dimostrazione di un teorema è la strada per esibire gli argomenti che supportano questa nostra convinzione. Non è un fatto formale, ma è proprio parte integrante del nostro processo conoscitivo. A priori non c'è niente di evidente, se no non servirebbe una dimostrazione, nel teorema di Pitagora, o in quello dei 4 colori, nel fatto che i fluidi abbiano o meno dei vortici singolari o che esistano o meno infinite coppie di numeri primi gemelli. C'è una realtà sfuggente che sta lì da qualche parte e, da matematici, ci muoviamo a tastoni nel buio, collezionando piccoli progressi e tanti insuccessi, aggirando gli ostacoli con l'intuito e a volte con un po' di fortuna. Ma sempre come se fossimo bendati e incappucciati. Pensate: un ipercubo in duecentomila dimensioni, dei numeri che superano di miliardi di volte il numero dei secondi trascorsi dall'inizio dell'universo moltiplicati per quello di tutti gli atomi esistenti, uno spazio di dimensioni infinite di cui studiamo le valli e i passi di montagna (e sono tutte cose vere). Ma no, non ci pensate, perché queste cose, in realtà, sono percepibili solo in modo indiretto, attraverso similitudini, ossia le tracce che lasciano nella nostra percezione ordinaria, e che a volte, ma forse non per i matematici, si confondono davanti ai nostri occhi. E queste tracce ci danno il potere, o forse l'illusione, di conoscere l'oggetto che le ha prodotte.In letteratura vi sono personaggi, situazioni, a volte solo un'impressione, un movimento, una fissazione, che vivono di vita propria nella mente dello scrittore. Un romanzo è un generoso tentativo di trasmettere questa attività mentale, e il testo scritto è la traccia che seguiamo, noi e lo scrittore al nostro fianco, cercando di catturare la cosa o l'essere che l'ha disseminata. Chi lo sa cosa sono (e non chi sono) veramente Emma Bovary, Renzo Tramaglino o Anna Karenina e le loro storie. Anna, Renzo, Emma sono cose tradotte nel testo e ricostruite dal nostro atto di leggere. E questa “cosa”, la funzione che, sorretta dai personaggi e dalle situazioni, va dalla mente dello scrittore a quella del lettore, è la base stessa dell'atto letterario. Ci sono dei segni insomma, e qualcuno o qualcosa deve pur averli lasciati. Ma molto resta nel non detto, cose che verranno ricreate nella mente del lettore, e anzi forse leggere alla fine è proprio il lavoro di immaginare le cose non scritte, le cose invisibili e inaccessibili nel testo.Nel libro che recensiamo, “Un genio nello scantinato", Alexander Masters decide di occuparsi di entrambe le cose, matematica e letteratura. Ci presenta un'indagine abbastanza letteraria, la ricerca di un personaggio sfuggente, ma in qualche modo atomico e ineludibile, e il fatto che sia una persona realmente esistente a noi poco importa (e forse nemmeno a lui), anche se non smette mai di intervenire nel racconto. E poi c'è lo stesso personaggio sfuggente che è a sua volta il protagonista di un'altra indagine, questa volta a carattere matematico, il tentativo di capire un componente primario e anche lui atomico e ineludibile di una parte importante della matematica, un oggetto sfuggente, ma anche un oggetto matematico realmente esistente, cosa questa volta assolutamente non secondaria.
Ci sono dunque due storie. Quella del personaggio è apparentemente molto semplice. Si chiama Simon Norton, e fin da bambino è sempre stato straordinariamente bravo in matematica. Nonostante un sistema educativo abbastanza rigido, Norton è emerso con facilità, dimostrando un grande talento matematico, vincendo ripetutamente le Olimpiadi internazionali di matematica e riuscendo a laurearsi a soli 17 anni per entrare immediatamente dopo a Cambridge (UK) come dottorando sotto la guida del grande matematico John Conway. La sua passione è la teoria dei gruppi, e partecipa, insieme a Conway e al suo gruppo, alla stesura dell'Atlante dei Gruppi Semplici Finiti, un'eroica impresa di classificazione che conclude una lunga stagione di ricerca di decine di matematici sparsi per tutto il mondo. L'Atlante è pubblicato nel 1985, quando Norton ha 33 anni. Con il trasferimento di Conway a Princeton (USA) nello stesso anno, Norton cessa ogni rapporto lavorativo con l'università. Avendo dei soldi di famiglia, vive da allora in una casa a Cambridge, dando in affitto alcune delle sue stanze e animando campagne civili di miglioramento dei trasporti pubblici inglesi, in realtà il suo interesse principale nella vita. La sua abitazione è immersa in un totale disordine e passa le sue giornate facendo lunghe escursioni attraverso itinerari di bus e treni che solo lui riesce a dominare completamente. Qualche cosa è successo, non sappiamo cosa, ma la vita di Norton sembra stagnare nello scantinato in cui vive e che dà il titolo al libro.E poi c'è un'altra storia. La storia di un problema difficile, che Masters, aiutato dallo stesso Simon, prova lo stesso a spiegarci. Ci sono i gruppi, che sono degli oggetti matematici che permettono di descrivere le simmetrie. Una simmetria è una trasformazione che lascia qualcosa uguale a se stesso. Prendiamo un triangolo equilatero con la punta verso l'alto. Se lo giriamo in senso antiorario di 120 gradi, il nuovo triangolo è indistinguibile dal precedente. Lo stesso se lo giriamo di altri 120 gradi nella stessa direzione. Possiamo comporre questi movimenti tra loro, costruendo così una tavola delle moltiplicazioni di questo insieme composto da un numero finito di oggetti. Questo è un gruppo (molto semplice) delle simmetrie di un triangolo. Possiamo ripetere la cosa con tutte le figure regolari e non del piano e dello spazio, o anche in spazi di dimensioni superiori. Possiamo anche costruire gruppi che descrivono le permutazioni di un insieme finito di oggetti. Insomma, i gruppi sono degli insiemi con un'operazione invertibile (moltiplico e divido) che hanno un'unità (e qualche altra cosetta, ma lasciamo perdere). E poi successe che, mentre era in corso la classificazione dei gruppi elementari (privi di sottogruppi normali, ossia i costituenti fondamentali di tutti gli altri gruppi), ci si accorse che da tutte le classi dei gruppi conosciuti si staccavano 26 gruppi cosiddetti sporadici (perché proprio 26 nessuno lo sa). Quasi tutti furono trovati tra il 1860 e il 1975. Uno di questi ha una cosa come 1054 elementi (sic!) e per questo, e anche per la difficoltà di rappresentarlo, fu chiamato il gruppo “Mostro” (di FischerGriess). E mentre per gli altri gruppi è stato sempre possibile capire quale fosse una rappresentazione ridotta semplice del gruppo, per questo gruppo la cosa non è stata ancora possibile. E nel libro si fa capire che questo problema in qualche modo si agita ancora nella mente di Norton: trovare un oggetto, che per vari motivi deve vivere in uno spazio che abbia 196.883 dimensioni (sic!), il cui gruppo di simmetria corrisponda al “Mostro”.
Simon ci saluta. Masters ci dice che è un uomo felice.
Nel testo troviamo delle descrizioni della vita di Norton, delle gite che fa sugli autobus in giro per il Regno Unito, alternate con spiegazioni di base molto suggestive, con dei bellissimi disegni dell'autore, sui fondamenti della teoria dei gruppi. E ad un certo punto l'autore ci suggerisce qualcosa, un qualcosa che andando avanti nella lettura stavamo cominciando a capire anche noi.
“Risposta alla Domanda Biografica Fondamentale n. 74, sottosezione b), nella fattispecie: perché scrivere un libro su Simon? Perché lui sta alla biografia come il Mostro sta alla teoria dei gruppi: un problema ostico che nonostante tutto rappresenta un tipo atomico dell'essere, la particella elementare dei caratteri contorti.
Masters non scrive una biografia canonica, tutta da fuori, con una pretesa oggettività. Masters vive accanto a Simon e gli vuole bene, e questo loro incontro sarà destinato a modificarli entrambi in modo irreversibile. Nel suo saggio “Rhetoric and the Math Melodrama”, apparso su Science nel dicembre del 2000 (e purtroppo non ancora tradotto in italiano), David Foster Wallace analizza l'insorgere di una nuova forma di genere letterario, il melodramma matematico, che ha come centro un nuovo tipo di eroe, il genio matematico (reale o immaginario che sia). E scrive: “La strana paura e il disgusto che la matematica scolastica produce in così tante persone è ciò che rende l'emergere del Melodramma Matematico così avvincente: se questo tipo di narrativa fosse in grado di restituire vivacità alla matematica pura e comunicare al lettore medio l'estrema bellezza e la passione per questa disciplina, ne guadagnerebbero sia il lettore che la stessa matematica.” Poi però si lamenta che i romanzi che sta recensendo, “Lo zio Petros e la congettura di Goldbach” e “I numeri ribelli”, non siano all'altezza di tale missione, sia per la loro scarsa qualità letteraria, sia per l'intrinseca difficoltà di parlare di matematica ad un pubblico eterogeneo. A me sembra che il lavoro di Masters, anche se non proprio melodrammatico, anzi a tratti molto divertente, e con momenti di notevole intensità, qui siamo più dalle parti di una TAC effettuata ad una persona cara, non avrebbe scontentato Wallace. Io farei leggere i capitoli sulla teoria dei gruppi a coloro che dicono di non capire la matematica. Forse capirebbero quanto sia più difficile capire le persone.
“Un genio nello scantinato” di Alexander Masters (Adelphi 2013, trad. di Andrew Tanzi)
“L’America dimenticata” – Intervista a Lucio Russo
Chi ha "scoperto" veramente l'America? Il Vecchio Mondo sapeva della sua esistenza già ai tempi di Tolomeo? Abbiamo intervistato Lucio Russo, fisico, storico della scienza, titolare della cattedra di Calcolo delle Probabilità all'Università degli Studi di Roma Tor Vergata in occasione dell'uscita del suo nuovo libro: "L' America dimenticata. I rapporti tra le civiltà e un errore di Tolomeo" (Milano, Mondadori, 2013).[Dopo l'intervista... non andate via. Trovate infatti alcuni brani del libro scelti dall’autore]
Qual è la teoria riportata nel libro "L'America dimenticata" a proposito dei contatti tra le civiltà antiche e l'America?La novità essenziale del libro consiste nella dimostrazione che le fonti di Tolomeo conoscevano, con buona approssimazione, le coordinate delle Piccole Antille. Il libro individua poi nei Cartaginesi la probabile fonte di queste informazioni ed espone plausibili scenari riguardanti la durata e la natura dei viaggi transoceanici, nonché le ragioni che hanno espunto queste conoscenze dalla tradizione geografica di età imperiale e medievale. Vorrei però sottolineare la diversa natura delle mie affermazioni. Mentre credo che sul primo punto si possa parlare di una “dimostrazione” (naturalmente non nel senso matematico del termine, ma nel senso in cui è normalmente usato in questioni storiche o filologiche), per il resto espongo solo scenari plausibili.
Riporto una curiosità di un lettore, commento a una recensione del libro di Pietro Greco sull'Unità: Perché, secondo lei, nonostante i lunghi contatti di cui si parla nel libro, nessuna delle culture americane adottò gli animali domestici eurasiatici (galline a parte), la ruota, o meglio il carro, l'uso dei metalli e in particolare il ferro?Innanzitutto debbo dire che mi sembrerebbe lecito rispondere “non lo so”. Per dimostrare la realtà di un evento storico è sufficiente trovare una prova (o, ancora meglio, un certo numero di prove indipendenti) che esso sia avvenuto mentre non è necessario essere in grado di spiegare perché quell’evento non ha prodotto conseguenze che appaiono plausibili a eventuali critici.Ciò detto, bisogna osservare che in America non solo si sviluppò la metallurgia, ma anche alcune tecniche particolari (come quella della “cera persa”) talmente simili a quelle usate nel Vecchio Mondo da costituire, secondo alcuni studiosi, prove indipendenti di antichi contatti culturali. Inoltre nel libro sacro dei Maya quiché, il Popol Vuh, si parla di ornamenti di metallo come importanti “status symbol” di uomini del passato.Quanto alla ruota, come ricordo nel libro, le civiltà precolombiane la usavano per costruire modellini mobili: un altro forte indizio indipendente di contatti con civiltà che conoscevano il trasporto su ruote (si tratta di un caso tipico di ciò che nel libro chiamo una”nozione fossile”).Resta il problema della mancata importazione di animali domestici di grossa taglia. Si può osservare che certamente è più facile compiere traversate oceaniche con galline che con bovini o ovini. Perché le culture americane adottassero ovini o bovini occorreva che: 1) qualche navigatore del Vecchio Mondo prendesse la strana decisione di togliere spazio ad altro carico o a viveri per l’equipaggio per imbarcare animali di grossa taglia e il foraggio necessario per il loro mantenimento durante tutta la traversata; 2) alcuni indigeni americani accettassero stranamente questi animali sconosciuti in cambio di altra merce; 3) questi stessi indigeni, pur non conoscendo tali animali, invece di usarli come cibo, decidessero di nutrirli per permetterne la riproduzione. Questa successione di eventi è certamente molto improbabile. Del resto sappiamo che l’allevamento dei polli si è propagato dall’Asia all’America attraverso il Pacifico, mentre nulla di simile è avvenuto per grossi mammiferi. Bisogna peraltro osservare che nel libro si ipotizza che i contatti possano essere continuati per secoli, ma non che siano stati frequenti né intensi.
Quali sono le altre ricerche a carattere storico che potrebbero portare supporto alle sue tesi? Per esempio vede qualche connessione con il libro di Elio Cadelo "Quando i Romani andavano in America", uscito recentemente, in cui si parla di prove archeologiche e scientifiche che confermerebbero che i Romani abbiano attraversato l'oceano Atlantico raggiungendo l'America?Esistono molti libri che hanno sostenuto l’esistenza di antichi contatti transoceanici. I più numerosi sono libri sensazionalistici privi di attendibilità. Ne cito due a titolo d’esempio:
Barry Fell, America B.C.: Ancient Settlers in the New WorldPatrick Huyghe, Columbus Was Last: From 200,000 BC to 1492, A Heretical History of Who Was First.Vi sono poi alcuni libri molto seri, che riportano i risultati di ricerche originali. Io ho trovato particolarmente utili i tre seguenti:Carroll L. Riley, J. Charles Kelley, Campbell W. Pennington, Robert L. Rands (editors), Man across the Sea. Problems of PreColumbian Contacts, University of Texas Press, AustinLondon 1971.Victor H. Mair (editor), Contact and Exchange in the Ancient World, University of Hawaii Press, Honolulu 2006.Terry L. Jones, Alice A. Storey, Elizabeth A. MatisooSmith, José Miguel RamírezAliaga (editors), Polynesians in America, AltaMira Press, 2011.Credo che il mio libro sia complementare ai precedenti, in quanto è basato su una prova quantitativa, del tutto diversa dagli elementi finora presi in considerazione.Quanto al libro di Cadelo, si tratta di un contributo di carattere giornalistico, dedicato peraltro più alla navigazione nell’antichità che non al tema specifico dei contatti transatlantici. Vi sono riportati dati utili (io ne ho tratto un’interessante foto di una statuetta di epoca romana in cui è probabilmente raffigurato un ananas), ma anche idee molto personali. Ad esempio l’informazione che nell’antichità si conoscesse la forma sferica della Terra è presentata come una primizia in contrasto con la dottrina ufficialmente accettata dal mondo accademico.
Mi sembra di capire che le sue non sono congetture, ma vere e proprie dimostrazioni, il risultato di calcoli precisi partiti dall'errore di Tolomeo che era noto da tempo ma non è mai stato spiegato fino in fondo. E' così?Sì. Il principale argomento della dimostrazione può essere facilmente sintetizzato. Tolomeo, come alcuni suoi predecessori di epoca imperiale, identifica le “Isole Fortunate” con le Canarie, ma tale identificazione è evidentemente il frutto di un fraintendimento. Le “Isole Fortunate” (sulle quali esiste un’ampia letteratura che precede Tolomeo) non hanno infatti nulla delle Canarie: la loro latitudine media riportata da Tolomeo differisce da quella delle Canarie di 15° (quanto Napoli dista da località svedesi); inoltre sono allineate in direzione NordSud (la loro longitudine, secondo Tolomeo, differisce al più di un grado), mentre le Canarie si sviluppano nella direzione EstOvest; anche le caratteristiche climatiche e ecologiche sono completamente diverse: le Isole Fortunate sono dette così perché favorite da un clima mitissimo e coperte da vegetazione lussureggiante, mentre le Canarie non hanno tali caratteristiche.Poiché sappiamo che nei secoli che precedono Tolomeo vi era stata una grave perdita di conoscenze sull’Oceano Atlantico, la confusione tra isole di quell’oceano è del tutto plausibile. Sorge quindi il problema di identificare le originarie “Isole Fortunate” alle quali si riferivano le fonti di Tolomeo. Se, a parità di latitudine, ci si sposta verso ovest si trova un arcipelago con la stessa forma e la stessa estensione in latitudine e longitudine delle Isole Fortunate quali le trasmette Tolomeo e con le stesse caratteristiche climatiche ed ecologiche delle Isole Fortunate descritte dalle antiche fonti: le Piccole Antille. Supponiamo che le fonti di Tolomeo con il nome di Isole Fortunate intendessero riferirsi realmente alle Piccole Antille e che Tolomeo, accettando l’identificazione con le Canarie, comune ai suoi tempi, le avesse poste erroneamente alla longitudine delle Canarie. Poiché Tolomeo sa dalle sue fonti che le isole sono sul semimeridiano opposto a quello della capitale della Cina, si spiega allora sia la sua sistematica dilatazione delle differenze di longitudine sia, di conseguenza, la sua sottovalutazione delle dimensioni della Terra. Poiché in entrambi i casi la verifica può essere quantitativa e notevolmente accurata, mi sembra che vi possano essere pochi dubbi sulla validità della ricostruzione. Credo che si possa parlare di “dimostrazione”, anche perché due altre strade indipendenti, anch’esse quantitative, che qui ometto per brevità, convergono allo stesso risultato.
Secondo lei la sua teoria ha ancora aspetti controversi che potranno essere chiariti da ulteriori ricerche?Io distinguerei nettamente due piani. Sul punto precedente (ossia sull’attribuzione alle Canarie di coordinate tratte da fonti che si riferivano alle Piccole Antille) sono ragionevolmente convinto di avere chiuso una questione. Naturalmente la possibilità di avere fatto un errore non può mai essere esclusa completamente. Perché mi convinca di avere sbagliato dovrei però ascoltare argomenti solidi. Finora non ne ho sentito nessuno.L’identificazione delle originarie Isole Fortunate con le Piccole Antille, implicando rapporti tra paesi
mediterranei e località dell’America centrale, solleva naturalmente un mare di questioni aperte, sulle quali nel libro ho solo cercato di abbozzare alcuni scenari di risposte possibili; sono convinto che la natura e la durata dei contatti e soprattutto la loro incidenza culturale siano tutte questioni aperte di enorme interesse.
Può parlarci meglio delle ricadute filosofiche delle sue ricostruzioni sull'evoluzione convergente delle società umane?Molte civiltà hanno percorso un tragitto essenzialmente identico che da una cultura paleolitica di cacciatoriraccoglitori, attraverso l’introduzione dell’allevamento, dell’agricoltura, della ceramica, della tessitura e successivamente dell’architettura in pietra e della metallurgia, è approdato alla civiltà “storica”, caratterizzata da specializzazione del lavoro, città, scrittura e organizzazioni statali. Per capire la natura dell’uomo e della cultura è essenziale capire se lo stretto parallelismo di queste evoluzioni è dovuto ai contatti tra le civiltà o a una sorta di determinismo biologico, che costringe ogni società umana ad evolversi alla stessa maniera. L’archeologia degli ultimi decenni ha mostrato che nell’ambito del Vecchio Mondo tutte le civiltà che hanno condiviso l’evoluzione prima accennata erano tra loro in contatto, diretto o indiretto, da tempi antichissimi. Poiché alcune civiltà mesoamericane hanno seguito un percorso sostanzialmente simile, la questione dei contatti precolombiani è diventata cruciale per scegliere tra le due alternative precedenti. Se si crede che le Americhe siano rimaste in un sostanziale isolamento culturale sin da quando furono popolate da popolazioni di cacciatoriraccoglitori provenienti dall’Asia è inevitabile accettare il determinismo biologico. Credo che il mio risultato, pur essendo lontano dal dimostrare l’ipotesi opposta (per questo bisognerebbe dimostrare che vi siano stati contatti antichi e profondi) riapra la questione.[intervista di Stefano Pisani]
***********Brani scelti da L’America dimenticata (per gentile concessione dell'Autore): Il problema di fondo(pp. 4041) Nella Mesoamerica, proprio come in Eurasia, sono apparsi allevamento e agricoltura, ceramica, tessitura e metallurgia, città, scrittura, sacerdoti e Stati, e, come vedremo, anche molti specifici prodotti culturali eguali fin nei dettagli a quelli elaborati nel Vecchio Mondo. Poiché nulla di tutto ciò poteva essere conosciuto dai cacciatori del paleolitico che, attraversando l’istmo che oggi è sostituito dallo stretto di Bering, avevano iniziato a popolare le Americhe, il Nuovo Mondo è stato usato come un gigantesco laboratorio in cui si dimostrerebbe la presenza di leggi universali che governano l’evoluzione di tutte le società umane in un’unica direzione. L’argomento è naturalmente basato sul presupposto (spesso assunto implicitamente come ovvio) che gli oceani abbiano costituito una barriera invalicabile, assicurando l’assoluto isolamento culturale del continente americano. Qualche traccia di antichi contatti(pp. 5556, 58) il libro sacro detto Popol Vuh, che racconta la storia dell’origine del popolo Maya Quiché, contiene tracce di antiche relazioni con popolazioni sull’altro lato dell’Atlantico? La risposta dipende dall’interpretazione del testo. Riportiamone alcuni passi:Vi furono molti sacerdoti e sacrificatori, non ve ne furono solo quattro, ma quei quattro furono i progenitori di tutti noi, popolo quiché. […] In Oriente si moltiplicarono. […] Vi erano in gran numero uomini neri e uomini bianchi, uomini di molte classi, di molte lingue, che destava meraviglia ascoltare. Non è chiaro però come essi passassero il mare: lo attraversarono e giunsero da questa parte, come se esso non fosse stato mare. […]In questo modo avvenne la sparizione, la fine di BalamQuitzé, BalamAcab, Mahucutah e IquiBalam, i primi uomini che erano venuti dall’altra parte del mare, donde sorge il sole.(pp. 6061) Se veramente gli «uomini neri e uomini bianchi, uomini di molte classi, di molte lingue» […] dei quali il Popol Vuh conserva il ricordo come antichi progenitori dei Maya Quiché fossero venuti dall’altra parte del mare, e se inoltre questi lontani progenitori avessero dato un contributo genetico significativo alle popolazioni Maya, gli studiosi di genetica delle popolazioni dovrebbero essere in grado di verificarlo. In effetti le analisi effettuate sul genoma delle popolazioni native americane non mostrano alcun contributo proveniente da popolazioni non americane, tranne una sola eccezione: i Maya, al cui corredo genetico hanno contribuito significativamente antenati «toscani» e Bantu.[…] Poiché si è sempre ritenuto che la sifilide sia stata importata in Europa dall’America dopo il 1492, si
può immaginare che se nell’antichità vi fossero stati contatti non sporadici anche allora si sarebbe dovuta avere la stessa spiacevole conseguenza. La scoperta di numerosi casi di sifilide in epoca romana può quindi sembrare una conferma di contatti precolombiani, […](p. 63) In definitiva molti dati di natura biologica sono coerenti con l’ipotesi di antichi contatti tra Vecchio e Nuovo Mondo e sembrano avvalorarla in modo significativo, ma nessuno ne ha fornito una dimostrazione accettata come tale dalla comunità scientifica.(pp. 6566) Il caso della terracotta romana trovata nel 1933 in Messico in una sepoltura precolombiana, che varie testimonianze affidabili hanno certificato intatta fino al ritrovamento, è forse l’unico che non sembra poter lasciare alcun dubbio. Ciononostante anche questo ritrovamento non è logicamente incompatibile con l’assenza di contatti. Si può sempre sostenere infatti, come è stato fatto, che l’oggetto potrebbe essere stato trovato sul relitto di una nave i cui occupanti fossero tutti morti prima di toccare le sponde americane. Pur di scongiurare l’eventualità di un contatto transatlantico, si è anche suggerito che la terracotta potrebbe aver raggiunto il Messico attraversando tutta l’Asia e l’Oceano Pacifico Il collasso culturale del II secolo a.C.(p. 75) A metà del II secolo a.C. il mondo mediterraneo visse una catastrofe, culminata nel biennio 146145, che, interrompendo bruscamente uno straordinario sviluppo plurisecolare, provocò una gravissima perdita di conoscenze e soprattutto di strumenti intellettuali. […](p. 88) La testimonianza forse più agghiacciante su cosa accadde ad Alessandria riguarda la sua istituzione culturale più famosa: la celeberrima Biblioteca. […] All’epoca della crisi era guidata da uno dei principali filologi dell’antichità: Aristarco di Samotracia. Un papiro proveniente da Ossirinco, che riporta l’elenco dei capi della famosa istituzione, ci informa che quando, nel 145 a.C., questi, con tutti gli altri intellettuali, fu costretto ad abbandonare Alessandria, alla direzione della Biblioteca fu chiamato a succedergli un […] ufficiale dei lancieri.(p. 94) La sfera cristallina delle stelle fisse aveva perso la sua utilità quando si era capito che il moto diurno rigido delle costellazioni è un’illusione dovuta alla rotazione terrestre ed era stata perciò abolita già da Eraclide Pontico nel IV secolo a.C., lasciando in sua vece una superficie sferica teorica, utilizzata come modello matematico per localizzare le stelle. Dopo il collasso culturale, la sfera delle stelle fisse riacquistò tutta la sua pesante corporeità, nella quale crederà ancora Keplero nel XVII secolo.(pp. 9596) […] molti filosofi vissuti dopo il collasso culturale si dicono stoici, cioè seguaci di una delle principali correnti filosofiche ellenistiche, della quale Crisippo era stato il massimo esponente. Per cogliere la distanza tra la corrente originaria e gli epigoni che si fregiano dello stesso nome basta però leggere questo passo del principale rappresentante dello stoicismo di epoca imperiale, Epitteto:Ma io, che cosa voglio? Conoscere la natura delle cose e seguirla. Per questo cerco un interprete che possa spiegarmela; e quando ho appreso che Crisippo è in grado di farlo, ricorro a lui. Ma non capisco le cose che ha scritto; allora cerco un interprete.Capire Crisippo era diventato altrettanto difficile che svelare la natura delle cose. […]Il crollo fu ben più devastante di quanto può apparire dagli esempi fatti fin qui. Agli intellettuali latini che un paio di secoli più tardi cercarono di occuparsi di scienza non mancavano solo i metodi che avevano permesso di ottenere risultati raffinati, ma anche gli strumenti concettuali di base indispensabili per capire il significato dei risultati più elementari. È quindi inevitabile la nascita di gravi equivoci. Quando per esempio Plinio descrive popolazioni i cui piedi avrebbero anteriormente il calcagno e posteriormente le dita, è chiaro che espone un’idea generata da un grossolano fraintendimento del concetto di «antipodi».(p. 98) La perdita delle conoscenze [geografiche] non riguardò solo le metodologie scientifiche della geografia matematica e della cartografia, ma anche informazioni qualitative su paesi e popoli, che spesso risalivano a epoche molto antiche. Il mondo mediterraneo si chiuse su se stesso e furono in larga misura dimenticate le conoscenze sulle regioni del mondo non incorporate nel dominio di Roma. Spesso scomparve, o sfumò nel leggendario, anche il ricordo dei viaggi del passato, che apparvero incredibili a chi non era più in grado di ripeterli. […] L’errore di Tolomeo(p. 151) Nel settore della geografia uno degli effetti più appariscenti della cesura culturale che separa Tolomeo dagli studiosi ellenistici è il rimpicciolimento della Terra. Tolomeo non attribuisce alla circonferenza terrestre i 252.000 stadi di lunghezza che Eratostene aveva misurato e Ipparco accettato, ma solo 180.000. Questa contrazione compensa la sua sistematica dilatazione delle differenze di longitudine,
cosicché le distanze lungo i paralleli per Tolomeo sono le stesse delle sue fonti ellenistiche. È quindi evidente che dilatazione delle longitudini e contrazione delle dimensioni della Terra sono due aspetti di un unico errore. […]Il principale risultato (per dare un’idea degli argomenti con cui è stato ottenuto se ne riporta il breve riepilogo finale)(pp. 209211) Credo che si debba considerare certa l’affermazione seguente.(A) Nelle fonti di Tolomeo con il nome di Isole Fortunate si intendevano le Piccole Antille, mentre successivamente (in particolare da parte di Tolomeo stesso) queste isole erano state erroneamente identificate con le Canarie.Poiché il metodo con cui il risultato (A) è stato ottenuto è insolito in storiografia, vale la pena riepilogare le ragioni che lo rendono in pratica certo. Da (A), che è coerente con le nostre conoscenze storiche e in particolare con il crollo delle conoscenze geografiche relative all’Oceano Atlantico verificatosi dopo la distruzione di Cartagine, discendono come conseguenze questi fatti documentati:1. Tolomeo attribuisce alle Canarie le latitudini delle Piccole Antille, commettendo un errore enorme: in media circa 15°.2. Tolomeo assegna all’arcipelago delle Canarie (che si estende soprattutto in direzione estovest) l’ampiezza di un solo grado di longitudine e 5,5° di latitudine, cioè con buona approssimazione le dimensioni delle Piccole Antille.3. Poiché le sue fonti collocavano le Isole Fortunate sul semimeridiano opposto a quello delle località asiatiche più orientali di cui si aveva notizia, l’errata identificazione delle isole porta Tolomeo a dilatare l’ampiezza in longitudine dell’Eurasia, e di conseguenza tutte le differenze di longitudine, di un fattore vicino a 1,4.4. Dal punto precedente e dalle distanze note lungo i paralleli Tolomeo deduce la misura della Terra di 500 stadi per grado di cerchio massimo, invece di quella di 700 stadi per grado che era stata determinata da Eratostene (e che, con metodi statistici, abbiamo dimostrato avere un errore non superiore a circa il 2%).5. Tolomeo, contando le longitudini a partire dal meridiano passante per le Isole Fortunate, è indotto dall’errata identificazione delle isole a sbagliare la longitudine di Tule, che nella sua fonte era la longitudine dell’intersezione del circolo polare con la costa orientale della Groenlandia.6. Ipparco [che è con ogni probabilità la fonte da cui Tolomeo trae le coordinate delle Isole Fortunate], estendendo la larghezza del mondo conosciuto per includervi le Piccole Antille, aveva aggiunto 26.000 stadi, lungo il parallelo di Atene, alla larghezza dell’ecumene calcolata da Eratostene, come in effetti afferma Plinio in un passo risultato finora incomprensibile (nel quale confonde la misura dell’ampiezza dell’ecumene con quella della circonferenza massima della Terra).Per nessuno dei sei punti precedenti era stata proposta alcuna plausibile spiegazione e in ciascuno di questi casi la verifica ha potuto essere quantitativa e notevolmente accurata. La probabilità che ciò sia accaduto per caso in tutti e sei i punti precedenti è del tutto trascurabile.Inoltre (A) permette di spiegare:7. perché Tolomeo (come è chiaro dalla cartina a p. 185) abbia dovuto ritrarre verso oriente le coste occidentali dell’Africa;8. perché Tolomeo (come è chiaro dalla stessa cartina) sia stato costretto a dilatare verso est l’estensione della Scozia e conseguentemente anche quella dello Jutland;9. le testimonianze di Orosio, Procopio e altri su Tule (riportate a pp. 176177), che finora erano risultate incomprensibili o giudicate fantasiose.La forza dei punti precedenti è tale che per la certezza dell’affermazione (A) non sarebbero necessarie né l’ulteriore conferma data dalla testimonianza di Simeone Seth, che conserva le affermazioni fraintese da Tolomeo, né le descrizioni pervenuteci delle Isole Fortunate, che sono così coerenti con l’identificazione ottenuta da aver fatto proporre sulla loro sola base l’ipotesi che potesse trattarsi di isole dei Caraibi Per concludere…(pp. 218219) La dimostrazione degli antichi contatti transoceanici è interessante soprattutto perché elimina il principale pilastro a fondamento della teoria dello sviluppo parallelo di tutte le civiltà attraverso le stesse fasi. Se la storia umana consistesse in una serie di evoluzioni parallele, progressive e lineari, rette da leggi definite, allora tutte le culture sarebbero ordinabili secondo una scala universale, ottenuta trasferendo in impliciti giudizi di valore un dato virtualmente cronologico (un po’ come si fa parlando di «età mentale» dei ragazzi). Accettando questa tesi sarebbe naturale considerare «primitive» le culture diverse dalla nostra (con
inconfessati, ma probabilmente inevitabili, impliciti giudizi razzisti sulle etnie «ritardatarie»).Diviene invece ora concepibile, anche se certamente tutt’altro che dimostrato, che la storia umana, proprio come l’evoluzione biologica, sia il risultato di una serie di eventi impredicibili e largamente casuali, che hanno disegnato particolari percorsi tra i tanti possibili, uno dei quali ha portato alla forma di civiltà alla quale siamo abituati, oggi egemone a livello planetario. […]Il venir meno di un supposto unico percorso prestabilito di evoluzione ridarebbe alla storia passata tutta la sua complessità e all’umanità attuale l’enorme responsabilità di scegliere liberamente gli sviluppi futuri.
***
Angolo Arguto
A che serve la matematica? La domanda dalle cento risposteTraduzione, con pregevoli licenze, dell’articolo A quoi ça sert, les maths? a cura di Kees Popinga. Se si è professore di matematica, matematico, studente di matematica o semplicemente genitore di uno studente, inevitabilmente ci si dovrà confrontare con LA grande domanda: a che cosa serve la matematica? Che si presenti sotto la forma di “A che cosa serve la trigonometria / il calcolo degli integrali / sapere che apiùbialquadratougualeadaduepiùdueabipiùbidue?” o nella variante affermativa “Ad ogni modo, la matematica non serve a niente”, il senso è sempre lo stesso. A che diavolo può servire la matematica?
Caso del giorno : Andrea, 14 anni, vi fa la domanda “a che cosa serve la matematica?” Come rispondergli? Scegliete tra 100 possibilità!1. Risposta topologicaPer sapere come contare i buchi della kesima dimensione dell’iperscatola di un pacchetto toroidale di patatine di dimensione 7.2. Risposta “specchio riflette”E tu, tu a che cosa servi?3. Risposta tecnofilaHai presente Google? Senza la matematica sarebbe ancora come Altavista. Hai presente il tuo cellulare? Senza la matematica sarebbe ancora un telegrafo. Hai presente Internet? Senza la matematica sarebbe ancora un fax. Hai presente l’ultimo Harry Potter in 3D? Senza la matematica sarebbe in 2D, in bianco e nero e con un tizio che suona il piano in sala. Hai presente il nuovoSupermario sulla console Nintendo 3DS? Senza la matematica, giocheresti ancora a Tetris. Hai presente la qualità dei suoni sul vinile? Senza la matematica, sarebbe… niente, rimarrebbe la stessa grande qualità.4. Risposta molto pratica la domenica dalla ziaA tagliare una torta come si deve! Prendendo il coseno dell’angolo di taglio desiderato e riportandolo sull’asse delle ascisse, si può…5. Risposta ZenLa risposta è dentro di te.6. Risposta in malafedeE tu come faresti a misurare l’altezza di un albero senza la trigonometria?7. Risposta emotivaGrazie alla matematica io faccio il professore di matematica e porto a casa uno stipendio. Non è molto, è vero, ma almeno posso mantenere mia moglie, disoccupata da nove anni, e i miei tre figli. Tanto più che il piccolino ha il mal di denti e che, con un po’ di economia, spero di poterlo portare dal dentista entro cinque o sei mesi. Sai, a me nessuno ha mai regalato niente…8. Risposta in malafede (bis)Bene. Immagina di essere rapito, con altre 99 persone, da un dittatore sanguinario che ti mette alla prova. Siete chiusi tutti assieme in un edificio e a ciascuno viene attribuito un numero diverso da 1 a 100. A turno, sarete condotti nella sala della libertà, che possiede 100 porte, numerate da 1 a 100. Dietro ciascuna porta si trova un numero, tra 1 e 100, che è stato in precedenza scelto in modo casuale. Se aprirete la porta che nasconde il vostro numero, resterete in sospeso. Altrimenti è la morte assicurata. Nella sala della libertà avrete diritto a 50 tentativi, non uno di più. Potrete comunicare tra di voi prima di entrare nella grande sala, ma non dopo. Che fate? Un ulteriore dettaglio: se uno di voi non trova il suo numero, tutti saranno condannati a morte. Una situazione come questa può capitare e, senza la matematica, non ne potrete mai uscire vivo…9. Risposta culturaleLa matematica serve tanto quanto conoscere i personaggi principali dei Promessi Sposi: è il bagaglio culturale necessario per essere una persona degna d’interesse. È poco probabile che la trigonometria, la fattorizzazione dei polinomi o la crescita della funzione logaritmica ti servano a una qualsiasi cosa, ma non meno di conoscere l’opera di Shakespeare o di Bach, perché è poco probabile che diventerai scrittore o compositore. La matematica fornisce una cultura come un’altra, da non giudicare in base all’utilità..10. Risposta nostalgica
Francamente, rimpiangi davvero i tempi in cui era il latino che serviva ad aprire le porte alle università più prestigiose?11. Risposta geekServe per apprezzare a fondo tutto il potenziale comico di xkcd o di un episodio di The Big Bang Theory o di Futurama...12. Risposta autoreferenzialtautologicaPer fare matematica!13. Risposta fisicaLa matematica serve per fare i cellulari, con tutte quelle storie di campi elettromagnetici e le equazioni di Maxwell che vi sono associate. La matematica serve a fare i microscopi a effetto tunnel, con l’algebra lineare non commutativa della meccanica quantistica. La matematica serve per fare le eliche che muovono le navi, o i motori che fanno volare gli aerei, con la meccanica dei fluidi e la famosa equazione di NavierStokes.14. Risposta “la natura è meravigliosa” (detta anche “Risposta hippy”)Guarda la bellezza della natura! Grazie alla matematica si può capire che il mondo che ci circonda è fatto di curve e di frattali! Osserva il cavolfiore: nel migliore dei casi non ci vedi che un legume in più da mettere nella minestra… io vedo soprattutto la sua struttura frattale, i suoi disegni ricorsivi. Osserva la pancia flaccida di tuo padre. Tu ci vedi dei cuscinetti di grasso? Io ci vedo l’espressione delle cicloidi!15. Risposta “messa in discussione del sistema scolastico”A che cosa serve la matematica? A che cosa serve la filosofia? A che cosa serve la geografia? A che cosa serve l’educazione fisica e sportiva? A che cosa servono le scienze della vita e della terra? A che cosa serve la fisica? A che cosa serve la storia? A che cosa servono le arti plastiche? A che cosa serve la chimica? A che cosa serve la musica? A che cosa serve l’educazione civica, giuridica e sociale? A che cosa serve l’italiano? A che cosa servono le scienze economiche e sociali? …16. Risposta “magica”A farti passare per un mentalista di fama, mentre ti sei limitato ad applicare un criterio di divisibilità per 9, a imparare un quadrato magico o a descrivere un’equazione algebrica che si semplifica perx.17. Risposta infantilePerché, perché? Perché uno più uno non fa tre. 18. Risposta aggressivaE chi se ne frega di sapere a che cosa serve? Fai gli esercizi! Più in fretta. E chiudi il becco!19. Risposta misticaSe un giorno troverai la risposta a questa domanda, allora sarai un matematico e, per questo motivo, non farai mai più matematica con questo scopo.20. Risposta utopicaUn giorno la maggior parte delle persone conoscerà il linguaggio matematico, più nessuno avrà paura delle formule algebriche. I media affronteranno allora i grandi temi con una concisione scientifica, la sola che consente di parlare in modo semplice delle questioni difficili. Sarà raro trovare sui giornali degli articoli di economia senza equazioni, mentre sarà comune vedere al Tg delle otto un grande ricercatore del CERN che ci aggiornerà sulla sua ultima grande scoperta. Quel giorno sarà bene esserci.21. Risposta monologoNon so se lo avete notato, ma la matematica non serve a niente! Non sto scherzando, non serve a niente! E a voi è servita a qualcosa? Non sto scherzando! Per esempio, il compasso… Avete già utilizzato un compasso, voi? Non so nemmeno a che cosa serve, io! E le radici quadrate vi hanno già fatto uscire da qualche casino? Ecco, per me è tutto, era uno sfogo.22. Risposta alla FermatPosseggo una bellissima risposta per la tua domanda, ma ci rimane poco tempo e la campanella sta per suonare.23. Risposta dimostrativaA dimostrare delle cose in maniera rigorosa. Ma anche a dimostrare che certe cose non possono essere dimostrate, e questa è una bella cosa. Ma anche a dimostrare che la dimostrazione che prova che certe cose non sono dimostrabili è corretta (e che, di conseguenza, esistono senza dubbio delle cose non dimostrabili). E questa è una gran bella cosa.24. Risposta da 2 di mediaA farsi 4 r15@te!1 Lol!
25. Risposta antiesotericaA sapere ciò che rientra nel campo della matematica oppure no. È vero: il numero aureo rientra di rado nella matematica, così come la successione di Fibonacci. Se un negoziante di profumi o di caffè ti vende le virtù estetiche del numero aureo o la perfezione della successione di Fibonacci, senz’altro sta cercando di infilare della scienza dove non c’è altro che aria fritta.26. Risposta “torna tra 10 anni”E già! Tu non sai nemmeno che cos’è la matematica, scimunito!27. Risposta pecuniariaA fare soldi! O, almeno, a non perderne giocando ai giochi d’azzardo come il Lotto, dove tenterai di applicare la legge dei grandi numeri a dei numeri piccoli (e perciò non funziona).28. Risposta “alla faccia!”La matematica è obiettiva, eterna e assoluta. Perciò è assai utile per legittimare un argomento filosofico con una retorica più o meno sofisticata.29. Risposta evasivaAltre domande?30. Risposta finanziaria (invero anche questa piuttosto evasiva)Fase 1: Sapere la matematica.Fase 2: …Fase 3: Profitti.31. Risposta Indiana JonesNon si può proprio giudicare la matematica in termini di utilità. D’altronde, la maggior parte dei matematici non ragionano in termini di utilità. Ciò che si cerca quando si fa matematica è piuttosto di esplorare mondi di cui non si sospetta né l’esistenza né la dimensione. Il matematico è un avventuriero che esplora nuovi territori, tranne che la ricompensa non è l’Arca Perduta, ma nuovi teoremi e profonde congetture.32. Risposta “Elementare, Watson!”A risolvere degli enigmi! La matematica è fatta di enigmi e, quindi, di piacere. Il piacere di cercare un po’, il piacere di cercare a lungo, la sofferenza di cercare troppo a lungo ma, alla fine, la liberazione di trovare! (Seguita dal dispiacere di aver passato così tanto tempo a cercare mentre la risposta era facile).33. Risposta minore di 3A utilizzare il simbolo <3 in modo diverso che alla fine di una frase sciocca e sdolcinata su richiesta.34. Risposta del parrucchiereA fare delle conversazioni appassionanti. Sei hai 50 anni, e non hai mai sbagliato un’uscita dell’autostrada a causa di una conversazione matematica troppo avvincente, sei vissuto invano.35. Risposta parmenidea alla “Marchese del Grillo”La matematica è, e non può non essere, e tu non sei un cazzo.36. Risposta Lavori PubbliciPer fabbricare delle cose. Quando si fa matematica, si fabbricano delle cose… tutti amano fabbricare delle cose! È grazie a delle buone fondamenta che possiamo costruire delle strutture matematiche…37. Risposta wignerianaSpiegami tu come mai la matematica è così efficace nelle scienze naturali. L’universo fisico può essere conosciuto nella sua struttura più profonda grazie alla matematica per il semplice fatto che è matematico, altroché!38. Risposta cognitivaA misurare l’intelligenza. La matematica è un indicatore abbastanza buono della precocità intellettuale, cosa che permette di separare il prima possibile il grano dal loglio. È triste. Ma è così.39. Risposta dell’allievo modelloAd avere dei bei voti! Si ha un bel dire, si ha un bel fare, ma è più facile avere dei bei voti trovando l’immagine del punto A per la rotazione di π/3 che ricordarsi tutti gli annessi e connessi della tettonica a placche e dei suoi effetti.40. Risposta esattaLa matematica costituisce la sola scienza esatta, dunque è l’unica che potrà consentire un giorno di capire il mondo che ci circonda.41. Risposta MinecraftA costruire aeroplani. A costruire delle tivù. A costruire delle bombe. A costruire degli ospedali. A costruire dei telefoni. A costruire delle maschere da sub. A costruire dei motori. A costruire delle automobili. A
costruire dei radar…42. Risposta alla domanda fondamentale sulla vita, l'universo e tutto quanto4243. Risposta statisticaIl 5% delle persone interrogate risponde “a niente”, il 10% “a qualche cosa”, il 15% se ne frega, il 25% “a risolvere problemi della vita di tutti i giorni”, il 20% “a fare riflettere”, il 25% “alla scienza” e, infine, il 7% delle persone interrogate pensa che la matematica permette di fare degli studi statistici che non stanno in piedi.44. Risposta ludicaA inventare dei giochi come Paroliamo.45. Risposta scientificaA praticare la scienza. La maggior parte delle scienze, in particolare la fisica, utilizza il linguaggio della matematica. Impossibile fare scienza senza conoscerne innanzitutto la lingua.46. Risposta in malafede (ter)Come piastrellare il pavimento di una stanza perfettamente rettangolare di dimensioni intere con delle piastrelle di dimensioni intere senza doverle tagliare? Senza calcolare il Massimo Comun Divisore è impossibile!47. Risposta contestualeA sbalordire i selezionatori durante un colloquio d’assunzione.48. Risposta tecnicaA provare che uno più uno è davvero uguale a due, e non altro (non si è mai al riparo da spiacevoli malintesi).49. Risposta intelligenteA imparare a riflettere! Avere metodo, essere logici e rigorosi non è sicuramente qualcosa d’inutile nella vita quotidiana e professionale, no?50. Risposta umanistaLa matematica è Scienza, e la Scienza non ha bisogno di essere utile, essa deve semplicemente esistere e crescere. La scienza è la conoscenza del mondo. Più questa conoscenza crescerà, migliore sarà il mondo.51. Risposta in malafede (quater)Immagina. Sei bloccato nel deserto senza calcolatrice e ti imbatti in un genio che ti propone tre desideri. Soltanto che non accetterà di esaudirli prima che tu abbia calcolato la radice quadrata di 181.413.961... Perciò, senza la matematica, puoi fare una croce sui tuoi sogni di ricchezza e di superpoteri…52. NonrispostaA che cosa serve? Perché ridurre la matematica alla sua utilità ? Sicuro, la matematica possiede un’utilità, ma bisogna davvero possedere una risposta a questa domanda per studiarla?53. Risposta a prioriA costruire tutto un mucchio di strumenti per ora senza interesse i quali, in piccola parte, si dimostreranno indispensabili in futuro. Poiché non sappiamo di che cosa sarà fatto il futuro, bisogna porsi un massimo di domande oggi per rispondere ai problemi di domani. La storia non manca d’esempi: l’aritmetica, creata per gioco, ha trovato applicazioni nella protezione delle transazioni bancarie; il GPS è un risultato dei millenni passati a fare geometria euclidea e poi iperbolica; la teoria dei grafi è in fin dei conti uno strumento perfetto per descrivere le reti; senza un oscuro teorema d’algebra, il più noto dei motori di ricerca non sarebbe che un elenco telefonico Web in più.54. Risposta a posterioriA rispondere alle domande che si pongono gli ingegneri o gli scienziati. Come farsi un’idea affidabile della composizione di un sottosuolo a partire da qualche carotaggio? Come migliorare in modo significativo l’affidabilità del trattamento dei dati meteorologici? Come dare un senso alle equazioni di YangMills? Non bisogna sicuramente aspettare che i fisici rispondano da soli a queste domande.55. Risposta machiavellicaA vincere tutte le partite di Potenza 4 al gioco del Nim o ad altri giochi imparziali.56. Risposta culinariaPer trasformare la ricetta di una torta al cioccolato per 4 persone in una ricetta di una torta alla vaniglia per 6 non c’è altra scelta che di utilizzare le percentuali e altre regole del 3. Che tu lo voglia o no, si tratta sempre di matematica (o forse solo dei calcoli…).57. Risposta infantile (bis)
A far parlare gli idioti.58. Risposta evasiva (bis)Serve, serve, ascolta me, che serve…59. Risposta da incompetenteCi voleva proprio, una disciplina della quale poter dire che non si è mai capito nulla, senza rischiare di passare per un incompetente.60. Risposta alla MontalbanoMi sono fatto persuaso che serve macari per contare le ammazzatine di una mesata a Vigata.61. Risposta regressivaChe cosa vuol dire “a che cosa serve la matematica”?62. Risposta interessataA guadagnare un mucchio di soldi! Tra i 10.000 euro e la celebrità che ricompensano le medaglie Fields e i milioni di dollari promessi a chi risolverà un problema da premio del millennio, la matematica può fruttare molto.63. Risposta artisticaA fare dei bei disegni con il computer e la teoria dei frattali senza aver bisogno di saper usare un pennello.64. Risposta filosoficaA fare dei ragionamenti. Né più né meno. Ma è carino fare dei ragionamenti. Si parte da quasi niente e si arriva a delle cose enormi… tutto ciò senza investire nient’altro che un po’ di tempo e di caffè. Non è per niente che, storicamente, la matematica discende dalla filosofia!65. Risposta rigorosaA essere rigorosi! La forza della matematica è che consente di acquisire i metodi che permettono di manipolare le idee di tutti i giorni. Il linguaggio, per esempio, richiede in fin dei conti molto rigore per evitare le incoerenze.66. Risposta psicologicaSecondo te, a cosa serve? Come mai ti stai facendo questa domanda?67. Risposta bourbakistaPrima di risponderti è meglio definire assiomaticamente i fondamenti della tua domanda.68. Risposta introspettivaCapire la matematica significa capire se stessi.69. Risposta alla PoincaréLo scienziato non studia la natura con uno scopo utilitaristico. Studia perché vi trova del piacere e vi trova del piacere perché la Natura è bella.70. Risposta ricettivaServe per sapere che se vuoi una vacanza tranquilla non ti conviene prenotare in un albergo di Hilbert.71. Risposta in malafede (quinquies)Immagina che un giorno vai dalla tua fornaia e che, al posto di dirti il prezzo della brioche, lei ti dice il prezzo di tre brioche e di due panini al cioccolato. In tale situazione, solo la matematica ti permetterà di sapere il prezzo della brioche da sola.72. Risposta da professionistaServe ad avere un basso numero di Erdős.73. Risposta topologica di tua madreA sapere come contare i buchi della k–esima dimensione di tua madre.74. Risposta giudiziariaA scrivere le leggi che governano la natura. L’umanità scrive le sue leggi nel Codice Penale, la natura scrive le sue nelle equazioni.75. Risposta oulipianaLa matematica serve a costruire il labirinto da cui ci si propone di uscire più tardi.76. Risposta a tuttoA rispondere a delle domande che non ci si sarebbe mai posti in un contesto diverso come “Perché le strade sono piane”? “Perché non esistono banconote da 2,62 euro?” o “Perché, se mi cade una fetta di pane imburrata, finisce sempre che il lato con il burro è sotto?”77. Risposta “apertura facilitata”A guadagnare in apertura mentale. Quando si passa tutto il tempo a generalizzare tutto, non si ha più paura di ciò che è diverso.
78. Risposta gergaleA poter parlare di “localizzazione dello spettro in approssimazione semi–classica nella teoria di gauge” così come mia madre parlerebbe di scrapbooking.79. Risposta cinefobaTu chiederesti davvero a un regista se il suo film serve a qualcosa?80. Risposta pasticceraA ridare alla ciambella il posto che merita nella società.81. Risposta diffidenteA imparare a diffidare delle apparenze. Si è a lungo creduto che tutti i numeri fossero razionali, fino alla scoperta della radice di 2. Si è a lungo creduto che due parallele non si incontravano, fino alla geometria proiettiva. Si è a lungo creduto che tutto era dimostrabile, fino a Gödel. Si è a lungo creduto che il Pd avrebbe vinto le ultime elezioni, fino a scoprire che le statistiche avevano dei margini d’errore.82. Risposta ereditariaA creare un’eredità per le generazioni future. La matematica odierna servirà ai ricercatori di domani. Le loro ricerche serviranno agli scienziati di dopodomani.83. Risposta scemaAd andare a letto meno scemi, ad andare a letto meno scemi, semplicemente questo.84. Risposta fai–da–teLa matematica non è altro che uno strumento. Io ti chiedo: a che cosa serve una pala se non c’è niente da scavare?85. Risposta per assurdoE tu, mi sapresti dire perché la matematica non serve a niente?86. Risposta contro–esempioLa matematica consente di capire che un solo contro–esempio basta a distruggere un’ipotesi. Così, non serve a nulla cercare 100 argomenti che provino che la matematica serve a qualcosa, quando ne basta uno.87. Risposta alla Chuck NorrisA contare tutte le volte che si vuole fino a 0.88. Risposta Mulino BiancoLa matematica è pratica in tutti i momenti della giornata, soprattutto al mattino. Se ci si è svegliati di cattivo umore, poco importa se immergiamo il plumcake nella tazza del caffè o viceversa. È poi molto pratica per poter dimostrare che si può tassellare un tavolino da colazione infinito con delle tartine esagonali. E poco importa il tipo di marmellata.89. Risposta disonestaA far bere qualsiasi cosa a delle persone oneste utilizzando degli argomenti tecnici pseudomatematici del tipo che la Terra è piatta, perché “essa gira, perciò si ha un effetto di forza centrifuga. Inoltre, il fenomeno è aumentato dalla componente verticale indotta dalla forza di Coriolis e la forza di marea della coppia TerraLuna, il che contraddice il differenziale della forza di gravità”.90. Risposta da giornalismo d’inchiestaA scoprire ciò che i grandi industriali ci vogliono nascondere, come la vera composizione del gelato gusto Puffo o il numero di frasi dei Baci Perugina esistenti.91. Argomentum ab auctoritateEinstein, almeno lui, conosceva l’utilità della matematica.92. Risposta CubeA uscire da un labirinto, nel caso poco probabile in cui ci si è fatti chiudere in un labirinto immerso nel buio. O nel caso ancor meno probabile in cui ci si è fatti chiudere in un labirinto cubico con certe camere mortalmente minate.93. Risposta astrattaImmagina un mondo in cui la matematica non esista. Riesci a capire a che cosa assomiglierebbe? No? Beh, io sì, io ci riesco, perché la matematica insegna l’astrazione!94. Risposta nicianaA nuocere alla stupidità.95. Risposta galileianaSe vuoi leggere il libro della natura devi conoscere il linguaggio con il quale è scritto, che è linguaggio matematico e i caratteri sono triangoli, cerchi ed altre figure geometriche.96. Risposta pitagorica
A che cosa serve? Ma se tutto è numero!97. Risposta letterariaA far credere che ci si interessi a Lewis Carroll per Alice, a Pascal per i suoi pensieri o a Guedj per il suo pappagallo.98. Risposta “che belle cose che dici”A concettualizzare l’eterno mistero dell’indicibile bellezza del mondo.99. Risposta praticaA scrivere dei grandi libri assai pratici per mettere in piano un tavolo o uno scaffale.100. Centesima rispostaPerché, se una domanda ammette così tante risposte diverse, vuol dire che il soggetto merita di sicuro il nostro interesse.Risposta psicodidattica (di riserva)Capisco la tua domanda, e in effetti è difficile dare una risposta se noi insegnanti continuiamo con un’impostazione della disciplina che non mette al centro il discente. È necessario valorizzare tutte le tue competenze, acquisite sia in modo formale sia in modo informale, perché tu possa comprendere pienamente l’utilità della matematica, che deve essere presentata come naturale evoluzione del tuo sviluppo psico–cognitivo e non come materia astratta e lontana dalla tua esperienza quotidiana. Ti soddisfa la mia risposta? Non vorrei mai pormi in termini conflittuali, sai…
Uno strepitoso post di Andrea Plazzi apparso sul blog di Leo Ortolani
****************************Carissimi rattofili e ortolanofili d’ogni dove,ho chiesto ospitalità a Leo per parlarvi del progetto COMICS & SCIENCE, che lui stesso ha già presentato e che sta piacendo molto. Ma davvero molto.E quasi non è ancora uscito.“Quasi” significa che da venerdì 25 ottobre potreste già trovarlo presso il Festival della Scienza di Genova (per la precisione, presso il Bookshop del Festival, ospitato da un visibilissimo container in Piazza De Ferrari), dove sicuramente sarà da sabato, quando lo presenteremo insieme a Leo.Poi naturalmente sarà a Lucca, presentazione compresa, e ci mancherebbe: se non è lì, dove dovrebbe essere?Per la precisione, lo troverete presso Lucca Comics Official (Padiglione Napoleone, stand E114), il nuovo stand ufficiale (l’avreste mai capito dal nome?) del Festival; il punto vendita cataloghi in cima alla scalinata di Palazzo Ducale, all’ingresso delle sale dedicate alle mostre (l’accesso è libero: non occorre avere biglietti, accrediti o braccialetti!); lo stand Panini (e anche questo vi coglierà di sorpresa, lo so); alcuni altri espositori doc, in via di definizione.Poi?Già: poi.Questo progetto è molto particolare, un numero per ora unico di un editore (il CNR; tutto vero!) che non ha mai operato nel circuito del fumetto. Naturalmente si sta attrezzando, e presto COMICS & SCIENCE sarà acquistabile online, ma nell’usuale circuito delle fumetterie per ora sarà reperibile solo presso alcuni negozi scelti, di cui pubblicheremo l’elenco dopo Lucca (quindi tenete d’occhio la pagina e il profilo FB).Sarà fondamentale il passaparola, e qui – non è una piaggeria pelosa, solo la verità voi potete davvero fare la differenza: dite agli amici interessati come e dove trovare COMICS & SCIENCE.E quelli di voi che saranno a Genova e a Lucca, se lo procurino anche per gli amici che non potranno esserci: trasformandovi in tanti piccoli GAO (“gruppi d’acquisto ortolaniano”) potete contribuire come nessuno a diffondere COMICS & SCIENCE.E a essere certi di procurarvi una pubblicazione di Leo che in ogni caso resterà unica.E comunque grazie a tutti: i lettori di Leo un ringraziamento lo meritano sempre, perché sono tra i più entusiasti e fedeli di tutto il fumetto italiano.Andrea Plazzi
Consistenza matematica, una storia abbastanza complicatadi Roberto Natalini
Il 15 ottobre 2013, Italo Calvino avrebbe avuto 90 anni e per celebrare il suo compleanno viene pubblicato il nuovo numero di Liberascienza, il magazine dell'omonima associazione, tutto dedicato alla "Consistenza". È l'ultimo numero di un piano editoriale che si è sviluppato negli ultimi due anni a partire dalle "Lezioni Americane" di Italo Calvino. Dopo Leggerezza, Rapidità, Molteplicità, Esattezza, Visibilità, la sesta e ultima tappa del viaggio in America è arrivata. Finalmente c'è Consistenza ("Consistency" nell'originale di Calvino, ma vedrete la cosa non finisce qui). Proponiamo di seguito il testo di Roberto Natalini sulla consistenza in matematica. L'intera pubblicazione è comunque scaricabile dal sito gratuitamente.
Certo non poteva mancare la matematica, parlando di consistenza. E mi sarebbe piaciuto proporre illuminanti connessioni tra matematica, filosofia e letteratura (e poi Calvino...). O ancora presentare una panoramica dei tanti significati che anche in ambito tecnico la parola “consistenza” prende in matematica, a partire dalla consistenza degli schemi di approssimazione numerica per le equazioni differenziali, che è forse l'unico argomento di cui potrei parlare con reale cognizione di causa. Oppure spiegare che in italiano la parola consistenza vuol dire “che ha sostanza”, mentre in ambito logicomatematico la parola consistenza è un solo un calco dell'inglese “consistency”, che dovrebbe in realtà essere tradotto con la parola “coerenza”(ma Calvino negli appunti in inglese scrive proprio consistency). E poi mi sono reso conto che tutti questi propositi sarebbero risultati futili o addirittura disorientanti rispetto al macigno che domina ancora oggi, a oltre ottant'anni di distanza, il panorama matematico quando la parola consistenza appare. Insomma, avremmo potuto conversare amabilmente del tempo sorseggiando la nostra tazza di tè, facendo finta di non vedere l'elefante seduto sul divano buono del salotto, ma alla fine l'unica cosa che avremmo ricordato del nostro incontro sarebbe stato l'elefante, appunto. Allora tanto vale parlare di lui, sperando che riusciate a digerirlo.###Supponiamo di fissare un sistema di assiomi, ossia alcune proposizioni che pensiamo debbano servire da fondamento non dimostrato di una teoria. Usando le regole di inferenza logica possiamo combinare questi assiomi per dedurre dei teoremi, ossia delle proposizioni che si dimostrano vere proprio a partire dagli assiomi. Il sistema di assiomi è detto essere “consistente” se non è possibile dimostrare, a partire dagli assiomi, che una certa proposizione e la sua negazione sono vere allo stesso tempo, ossia se non esistono affermazioni contraddittorie. Questa definizione di consistenza può risultare strana e allo stesso tempo abbastanza ovvia. È ovvia se vogliamo che il nostro sistema abbia un senso, ossia sia razionalmente accettabile. Anzi forse questa richiesta potrebbe essere posta alla base di ciò che chiamiamo razionale: non possiamo accettare che siano vere allo stesso tempo una cosa e il suo contrario. E inoltre questo negherebbe la possibilità di argomentare logicamente, poiché si può far vedere che se in un sistema esiste un'affermazione che è vera e allo stesso tempo è anche vera la sua negazione, allora è possibile dedurre qualsiasi cosa all'interno del sistema stesso. Questo principio è chiamato ex falso sequitur quodlibet (ossia, dal falso segue qualsiasi cosa). Vediamo come funziona. Supponiamo per esempio che siano vere contemporaneamente “4 è diverso da 5” e “4 è uguale a 5” e vogliamo dedurre l'affermazione “tutti gli asini volano”. Dato che “4 è diverso da 5” è vera, allora è vera anche l'affermazione D=“almeno uno dei due tra “4 è diverso da 5”e “tutti gli asini volano” è vera”. Ora sappiamo anche che “4 è uguale a 5”, per cui, per essere ancora vera l'affermazione D dobbiamo concludere che “tutti gli asini volano” è vera. Insomma, un bel pasticcio, con tutti questi asini volanti...Allo stesso tempo la consistenza è strana. Per la filosofia classica, per Aristotele, non esiste proprio il problema, non ci possono essere proposizioni vere e false allo stesso tempo e basta, o una cosa è vera o è vero il suo contrario, e non ci sono altre possibilità. Ma allora, a cosa serve parlare di consistenza, quando questa dovrebbe essere una cosa accettata da tutti?Il problema nasce dal fatto che mentre per i greci gli assiomi erano affermazioni considerate come evidenti, da non dimostrare, ma nemmeno da discutere, ossia una base di partenza da cui dedurre tutte le affermazioni “vere”, per noi moderni la cosa è leggermente più complicata. L'idea nuova, che risale alla fine del XIX secolo, è che la matematica si sarebbe dovuta sganciare da ogni considerazione esterna. Il programma di David Hilbert, uno dei grandi matematici vissuti a cavallo tra il XIX e il XX secolo, proponeva di
autofondare la matematica, partendo da una scelta opportuna di assiomi, senza far riferimento ad alcuna evidenza empirica. È un po' il programma di Euclide per la geometria, ma per Euclide le basi di partenza erano prese come evidenti, mentre per Hilbert è solo la matematica che deve decidere se un dato sistema di assiomi è legittimo o meno. Il secondo problema di Hilbert, proposto nel 1900, chiedeva proprio di dimostrare che l'aritmetica è basata su un sistema di assiomi che possiede queste tre proprietà, che sono quelle che lo rendono appunto legittimo:
a) Minimalità (o indipendenza): nessuno degli assiomi può essere dedotto dagli altri.b) Consistenza: non esistono contraddizioni interne al sistema, ossia ogni teorema dedotto dagli assiomi non può essere vero e falso allo stesso tempo.c) Completezza: si può determinare per ogni affermazione se essa o la sua negazione possono essere dimostrate a partire dagli assiomi.
Insomma, dato che adesso gli assiomi possono essere messi insieme in modo arbitrario (e in alcuni sistemi gli assiomi potranno apparire assolutamente non evidenti), la consistenza diventa una proprietà da richiedere e dimostrare, per evitare di costruire un inutile castello di carte.Come sistema di assiomi per l'aritmetica, venne considerato allora il sistema proposto nel 1899 dal matematico italiano Giuseppe Peano per descrivere i numeri naturali, che può essere scritto informalmente in questa maniera (non strettamente simbolica):
1. Esiste un numero naturale che chiamiamo 0 (zero).2. Ogni numero naturale n possiede un successore, che chiamiamo succ(n).3. Se due numeri hanno lo stesso successore, allora sono uguali.4. Lo 0 non è il successore di alcun numero.5. (Principio di induzione) Preso un qualunque sottoinsieme A dell'insieme dei numeri naturali tale
che lo 0 appartiene ad A e per ogni numero n, se n appartiene ad A, allora anche succ(n) appartiene ad A, allora A coincide con tutto l'insieme dei numeri naturali.
Immaginate di non sapere cosa siano i numeri (naturali) e provate ad usare solo gli assiomi per ritrovare tutte le loro proprietà conosciute (questo è un po' il succo degli assiomi, caratterizzare una certa parte della matematica con un numero limitato di affermazioni facili da accettare o rifiutare). Per esempio, partendo dagli assiomi, si può definire l'operazione di addizione in modo ricorsivo mediante queste due proprietà:
a) n+0=n;b) n+succ(m)=succ(n+m).
[Voi che state dormicchiando in penultima fila, sveglia! Per esercizio, provate a dimostrare che 2+2=4 usando gli assiomi e questa definizione (è semplice, ma non così semplice)]. I primi quattro assiomi sono abbastanza evidenti, se pensiamo a come sono fatti i numeri. Si parte da 0, e poi si va avanti con la funzione successore generando tutti i numeri. Tuttavia, se usassimo solo i primi quattro assiomi, non avremmo ancora il sistema dei numeri naturali, perché non riusciremmo a dimostrare tante proprietà che ci aspettiamo siano vere. Dobbiamo aggiungere un nuovo assioma, e Peano propose appunto il principio di induzione. Purtroppo questo principio non è un solo assioma, ma piuttosto equivale ad avere un numero infinito di assiomi, diciamo uno per ogni sottoinsieme dei numeri naturali. Ed è questo principio di induzione (anche se riproposto in alcune formulazioni più deboli) che porterà le maggiori complicazioni. Tuttavia, gli assiomi di Peano sembravano (e sembrano ancora) un buon punto di partenza per dare una descrizione sensata dell'aritmetica. Anzi Hilbert aveva dimostrato che praticamente tutta la matematica, analisi, geometria, algebra, poteva essere dimostrata consistente se lo era l'aritmetica data dagli assiomi di Peano. E Hilbert e tanti altri matematici erano abbastanza sicuri di poter dimostrare quest'ultimo passo appunto della consistenza dell'aritmetica di Peano. Invece, nel 1931, l'allora 25enne Kurt Gödel, uno studioso austriaco che frequentava il Circolo di Vienna, pubblicò un lavoro destinato a sconvolgere i piani del grande Hilbert. Gödel dimostrò infatti un primo risultato molto sorprendente, ossia che in qualsiasi sistema assiomatico consistente che sia sufficientemente potente da poter esprimere l'aritmetica, è possibile trovare delle proposizioni aritmetiche vere che non possono essere dimostrate a partire dagli assiomi. Ossia, supponendone la consistenza, l'aritmetica di Peano, e anche qualsiasi sua possibile estensione assiomatica, formano dei sistemi incompleti. Questo può sembrare molto strano, cosa vuol dire infatti che di una proposizione è vera e non è dimostrabile? L'idea di Gödel non può essere spiegata in poche righe, ma
dovendolo fare, basti accettare la possibilità di associare in modo unico a ogni successione finita di simboli, un numero intero. Questo permette di tradurre in operazioni numeriche qualsiasi affermazione e anche qualsiasi dimostrazione, ossia permette di parlare dei teoremi del sistema usando gli stessi numeri. Attraverso varie manipolazioni Gödel riuscì a scrivere una proposizione con questo enunciato: “Questa proposizione non è dimostrabile in questo sistema di assiomi”. Se la proposizione fosse falsa, allora sarebbe dimostrabile, ossia una contraddizione che porterebbe all'inconsistenza del sistema, e per questo motivo deve essere vera (e non dimostrabile).Purtroppo non era finita. Con gli stessi metodi Gödel dimostrò che se un sistema assiomatico è consistente e abbastanza potente da esprimere l'aritmetica, allora è impossibile provare la sua consistenza all'interno del sistema stesso. Ossia non è possibile basare la nostra convinzione nella consistenza dell'aritmetica sull'aritmetica stessa, ma dobbiamo basarci su un altro sistema di assiomi (più forte) per fondarla in modo non contraddittorio (e così via, anche per i nuovi sistemi, ovviamente...). La matematica, che da oltre mezzo secolo cercava di rendersi autonoma da qualsiasi considerazione esterna, risultava in ultima analisi legata ad un filo, quello della nostra intuizione sulla ragionevolezza delle ipotesi di base.È una cosa grave? I matematici di oggi pensano di no. Il programma di Hilbert ci appare come una delle tante possibili direzioni di ricerca, ma non come l'unica alternativa possibile. La matematica vive della sua plausibilità, tutti accettano gli assiomi di Peano e in particolare il principio di induzione, sono stati dimostrati alcuni teoremi finora ritenuti incredibili (il Teorema di Fermat, la congettura di Poincaré, il teorema di quattro colori, la congettura di Goldbach debole), e viviamo in un'epoca in cui la scienza e la tecnologia sono sempre più imbevute di matematica. Una matematica che si basa proprio sulle idee usate e inventate da Gödel. Se non ci fosse stato Gödel con i suoi teoremi, non avremmo probabilmente gli algoritmi di Google, il bancomat, la compressione dati dei telefoni cellulari, gli algoritmi di trattamento delle immagini mediche.Tuttavia, certo, un piccolo dubbio rimane. Perché, se è impossibile dimostrare la consistenza dell'aritmetica, fondandosi solo sull'aritmetica stessa, ossia non si può sapere a priori che non ci saranno contraddizioni nel sistema generato dagli assiomi di Peano, rimane sempre la possibilità dell'inconsistenza. Il teorema di Gödel non la esclude, e anzi ogni tanto spunta qualche matematico convinto di aver trovato una dimostrazione di questa inconsistenza (ma finora si sono tutti sbagliati…). Basterebbe trovare una esempio, un solo esempio per far cadere tutto il castello di carte della matematica. Cambierebbe molto? In teoria sì, tutto sarebbe vero e falso allo stesso tempo, ossia tutte le affermazioni sarebbero vere, e molte nostre certezze andrebbero in fumo. Oppure no, e scopriremmo che avevamo capito male qualche cosa di veramente importante. Ma questo è il bello della ricerca matematica.Viareggio, 1723 agosto 2013. [Ringrazio Giuseppe “Pino” Rosolini per l'attenta rilettura e gli amichevoli consigli. Tutte le imprecisioni sono tuttavia solo farina del mio sacco].
I luoghi della matematicaLa matematica è fatta anche di “luoghi”. Grazie ai nostri “inviati” speciali sul posto, conosciamo università, centri di ricerca, festival e altri luoghi e eventi in cui la matematica è protagonista.
[#16] Matematica & Informatica Lo Heidelberg Laureate Forum: dove i pulcini incontrano i Campioni
Leandro Arosio è assegnista di ricerca in matematica all’Università di Roma “Tor Vergata”. Si occupa di dinamica olomorfa in più variabili complesse. La sua partecipazione a questo evento è stata possibile grazie alla segnalazione e al sostegno dell’Istituto Nazionale di Alta Matematica.
di Leandro Arosio
È un’esperienza radicalmente diversa dai vari workshop o convegni a cui si è abituati quando si fa ricerca in matematica. La cosa migliore per iniziare a raccontarla è partire da un po’ di storia, e in particolare dai Lindau Nobel Laureate Meetings. Lindau è una piccola città tedesca sul lago di Costanza, dove nel ‘51 due medici tedeschi decisero di organizzare un incontro tra premi Nobel della medicina e giovani ricercatori per rilanciare lo scambio scientifico internazionale che ristagnava dopo il secondo conflitto mondiale. Da allora, con cadenza annuale, nella stessa cornice si sono alternati premi Nobel in medicina, fisica, e chimica, e l’evento è diventato (con parole loro) un “forum universalmente riconosciuto per il passaggio della conoscenza tra generazioni di scienziati”. Ora, è noto che non esistono premi Nobel per la matematica e per l’informatica. Una lacuna colmata (finora) da ben tre premi, altrettanto prestigiosi: i premi Abel, Turing e la medaglia Fields. I primi due sono a tutti gli effetti dei sostituti dei premi Nobel rispettivamente per la matematica e l’informatica. La medaglia Fields è in un certo senso l’intruso: viene assegnata ogni quattro anni dall’International Mathematical Union a matematici che non abbiano superato i fatidici quarant’anni (Wiles quando ha dimostrato il Teorema di Fermat li aveva da poco superati, quindi niente da fare) e la si può ritenere responsabile della leggenda urbana secondo la quale un matematico dopo i quaranta ha “già dato” (e se proprio non vuole andare in pensione, almeno dovrebbe dedicarsi a fundraising o simili). Lo Heidelberg Laureate Forum è un incontro modellato sui Lindau Meetings, in cui giovani ricercatori in matematica e informatica hanno la possibilità di avere un incontro ravvicinato con i vincitori dei premi Abel, Turing e Fields nella splendida città di Heidelberg. Lo slogan non lascia dubbi sulle intenzioni: “Laureates meet the next generation”. Sono stati invitati tutti i novanta Laureates viventi, e quasi la metà ha raccolto l’invito. Per quanto riguarda i giovani ricercatori, ne sono stati selezionati cento tra i matematici e cento tra gli informatici.
La macchina organizzativa: spazio anche per... l’OktoberfestL’ideatore e organizzatore di questo incontro è Klaus Tschira, il fondatore della nota software company SAP, che nel ‘95 ha creato una fondazione per promuovere la matematica e l’informatica. Tschira è un uomo molto appassionato, con una disponibilità di mezzi impressionante. In effetti la macchina organizzativa dell’HLF lavora a tempo pieno senza mai un’incertezza o una sbavatura. Tutto è stato predisposto nel migliore dei modi, a cominciare dai badge al collo coi cordini di diversi colori a segnalare chi fosse Laureato, ricercatore, ospite, giornalista, blogger, fotografo, membro dello staff o quant’altro. Limando minuziosamente i tempi morti del programma (e i tempi di riposo) sono riusciti a inserire nello spazio di una settimana venti lezioni plenarie, tre miniworkshop, due tavole rotonde, due cene in due diversi castelli, gita in barca, concerto a tema alla Stadthalle, visita ai centri di ricerca locali e perfino a ricreare una Oktoberfest con tanto di barile di birra e di danzatori bavaresi intenti a riempirsi di schiaffi a suon di musica.
Si comincia con la marcia trionfaleLa cerimonia di apertura inizia con un coup de théâtre che sfiora il kitsch. Nella sala principale della Neue Universität ricolma di giovani ricercatori i Laureati vengono fatti entrare, visibilmente imbarazzati, sulle note trionfali di “Pomp and Circumstance”. Poi una lunga serie di discorsi fortunatamente intervallata da quattro
sassofoniste uscite dal nulla che propongono godibilissimi classici jazzati. Tschira nel discorso d’apertura si lascia andare a un piccolo sfogo: troppi Laureati matematici avrebbero declinato adducendo motivi di salute, viene da pensare che la matematica faccia male. Piccata la replica della presidente dell’IMU, Ingrid Daubechies: cita una qualche statistica secondo la quale i matematici risultano essere i più felici del proprio lavoro, quindi esclude categoricamente che la professione sia nociva per la salute. Ovazione poi per Vint Cerf, presidente dell’ACM e premio Turing, che termina il suo intervento chiedendo a gran voce “La prossima volta direi di lasciar perdere “Pomp and Circumstance”, ma richiamiamo le sassofoniste!”.
Dalla cerimonia di apertura ci si sposta alla Stadthalle per il concerto. L’orchestra è quella della SAP, e lo spettacolo si chiama “Mozartiana con spirito scientifico” (sic). Due attori discutono animatamente sulla seguente questione: può il computer creare arte? Ad esempio può generare un brano di musica classica bello come quelli di Mozart? Fanno sentire due brani invitando il pubblico a capire quale sia quello di Mozart e quale sia quello generato dal computer. Il pubblico è diviso, ma, colpo di scena, entrambi sono generati dal computer. Tutto molto divertente, un unico dettaglio stonato: l’intero spettacolo è in tedesco, senza sottotitoli.
Villani superstarL’atmosfera tra i partecipanti è molto informale e rilassata, e questo è uno degli aspetti migliori del Forum. Cito dal discorso d’apertura di Tschira: “Lo scopo di questo Forum è costruire relazioni, trovare esempi e modelli, creare amicizie tra i vincitori dei premi e i giovani ricercatori”. Capita quindi spesso durante le pause tra i talk, oppure a pranzo e a cena, che si formino capannelli di ricercatori attorno a qualche Laureato che racconta aneddoti personali. La star in questo senso è indubbiamente Cédric Villani. Che sia in coda a mensa o durante la gita in barca, si sposta circondato da una nuvola di giovani interessati ai suoi racconti o semplicemente desiderosi di sapere perché porta sempre una spilla a forma di ragno (se la cosa incuriosisce anche voi, devo confessare che la sua risposta è stata decisamente elusiva). Tra i giovani ho notato con piacere una nutrita partecipazione di italiani, per poi apprendere con dispiacere che la maggior parte lavora all’estero.
La “classifica” delle lezioniQuanto alle lezioni, i Laureati sono stati lasciati completamente liberi nella scelta degli argomenti, con la sola preghiera di ricordarsi che la maggior parte del pubblico non conosceva nulla di quello di cui si occupano. Questo è stato a mio avviso fondamentale: nonostante non siano mancati i talk incomprensibili dall’inizio alla fine, la maggior parte dei Laureati ha cercato di far passare qualcosa a tutti. Nel mio piccolo è stato sorprendente riuscire ad apprezzare numerosi talk di informatica, di cui non so assolutamente nulla. Non potendo raccontare tutte le lezioni plenarie e i workshop, mi limito a darvi una mia personale classifica (a ogni modo tutte le lezioni sono registrate e si possono vedere gratuitamente sul sito dell’ HLF).
La più divertente: Reddy (Premio Turing)
Raj Reddy ha organizzato un torneo a eliminazione diretta tra i pretendenti al titolo “l’uomo che ha inventato il computer”. Partecipanti: Pascal, Leibnitz, Babbage, Atanasoff, Turing, Zuse, von Neumann e altri. Ha quindi proiettato una grossa matrice piena di YES e NO dove le righe corrispondevano ai partecipanti e le colonne ai requisiti che un computer deve soddisfare per definirsi tale, come l’essere programmabile, elettronico, binario, l’esistenza di un prototipo funzionante e quant’altro. Poi via con le eliminazioni: per primi ci lasciano Pascal, Leibnitz e Atanasoff per la mancanza di programmabilità. E così via tutti gli altri tranne Turing e Von Neumann che si affrontano nella sfida finale, vinta di misura dal primo. Conclude con un finale un po’ troppo buonista: in fondo hanno tutti diritto di fregiarsi del titolo “l’uomo che ha inventato il computer”.
La più Houdini: McMullen (Medaglia Fields)
Curtis McMullen ha deliziato i partecipanti del workshop sulla topologia quantistica con un trucco di “magia matematica”. Si tratta di attorcigliare una corda circolare attorno a due moschettoni aperti in modo
che quando chiudiamo i moschettoni il tutto sia legato assieme e non sia possibile sciogliere la corda dai moschettoni. Poi si agganciano assieme i due moschettoni e la corda cade al suolo tra lo stupore degli astanti. Oltre ad essere una freccia in più al vostro arco per provare a convincere gli amici che la matematica serve a qualcosa, è un bell’esercizio sul gruppo fondamentale. Infatti la corda resta legata perché il gruppo fondamentale del complementare dei due moschettoni non agganciati non è abeliano, mentre quando agganciamo i due moschettoni diventa abeliano. Qui potete vedere come si fa e perché funziona.
La più messianica: Voevodsky (Medaglia Fields)
Riguardo a questa lezione scenderò un po’ più nel particolare essendo quella che ha generato più “scalpore”. Dieci anni fa, cercando un nuovo argomento dopo aver vinto la medaglia Fields per i suoi lavori in teoria dell’omotopia, Vladimir Voevodsky si pone la seguente domanda (c’è chi può): “Di che cosa ha maggiormente bisogno la matematica per il suo sviluppo?” La sua risposta è che ha bisogno di un software che aiuti i matematici a controllare le dimostrazioni, in modo che possano andare a letto felici senza svegliarsi sudati nella notte avendo trovato un errore. Un interessante software di questo tipo esiste già: il francese Coq Proof Assistant, basato sulle teorie dei tipi di MartinLöf. Studiando Coq, se ne esce con una nuova semantica per queste teorie, direttamente mutuata dalla teoria dell’omotopia. Solitamente i tipi sono interpretati come una sorta di insiemi, e questo è il punto che non convince Voevodsky. Giunge alla conclusione che i tipi non sono insiemi, ma vanno interpretati come tipi di omotopia, e questo lo porta alla seguente considerazione generale: la matematica in realtà studia le strutture sui tipi di omotopia. Quindi un buon linguaggio che scriva matematica in modo che sia controllabile da un software deve essere un linguaggio che lavori sui tipi di omotopia. E, sorpresa, il linguaggio delle teorie di MartinLöf è adattissimo per questo nuovo approccio. Si mette quindi a formalizzare l’Algebra I di Bourbaki in questo linguaggio, e facendolo si convince di aver trovato la soluzione alla domanda che si era posto: un linguaggio che sia allo stesso tempo adatto agli uomini per lavorarci, e abbastanza formale per prestarsi alla verifica del software. È a questo punto che si rende conto che la teoria degli insiemi di ZermeloFraenkel non gli serve più, e che il suo approccio costituisce fondamenta completamente autosufficienti per la matematica: le chiama “Univalent Foundations”. La novità centrale è questa: mentre in ZermeloFraenkel una volta definito (ad esempio) il concetto di gruppo la maggior parte degli enunciati riguardanti gruppi non sarà invariante per isomorfismi (di gruppi), nelle Univalent Foundations ogni enunciato che coinvolga gruppi è automaticamente invariante per isomorfismi. La netta impressione che si ha è che Voevodsky sia sicuro che rivolterà la matematica come un calzino.
La lezione più stimolante: i consigli a un giovane matematico di Sir Atiyah (Medaglia Fields e Premio Abel)
Sir Michael Francis Atiyah ha carisma da vendere e tanta voglia di trasmettere la propria grande esperienza. Il titolo della lezione è una dichiarazione di intenti: “Consigli a un giovane matematico”. Inizia con un avviso che è un piccolo capolavoro: “Quella che segue è una visione personale basata sulla mia esperienza. Fortunatamente tra i matematici c’è una grande diversità, che serve a livello evoluzionistico per garantire una buona selezione. L’originalità, che è la più grande fonte di progresso si ottiene rompendo col passato e ignorando i consigli. Quindi io vi do i consigli, voi ascoltateli, ma non seguiteli”. I consigli toccano vari temi, ecco un breve sunto:
Da giovane anche Atiyah ha avuto paura di non farcela ed è stato vicino a lasciare la ricerca. Poi ha parlato con Serre (a suo dire il più grande matematico della sua generazione) che gli ha detto che anche lui ha avuto paura di non farcela ed è stato vicino a lasciare la ricerca. Insomma, è normale, e passa.
Si può addirittura azzardare che solo i mediocri sono eccessivamente sicuri delle proprie abilità: quanto migliori si è, tanto più in alto si tende a posizionare la propria asticella.
Non chiudetevi a pensare soli nel vostro ufficio: parlate con gli altri, collaborate coi vostri colleghi e amici.
Volete delle idee? Continuate a porvi domande: la curiosità è il motore della ricerca.
Fatevi una lista di esempi basati sul vostro background su cui testare le vostre idee. Serve a tenere i piedi per terra.
Non confondete il processo creativo con le dimostrazioni: quest’ultime sono un aspetto tecnico, l’ultima verifica di un’idea.
I problemi migliori su cui lavorare sono quelli che ci si è posti da soli. Quando si lavora su un problema posto da qualcun altro non si ha controllo sulla reale difficoltà e sul background del problema.
Createvi la vostra nicchia nella matematica, e mostratevi indipendenti.
Gli articoli scritti male vengono ignorati, quelli scritti bene possono diventare dei classici.
Per finire, un’ultima citazione che non è un consiglio ma merita di essere riportata: “non esiste la matematica pura, esiste solo quella applicata e quella non ancora applicata”.
Un rientro (quasi) feliceQuest’ultima lezione in particolare è un bell’esempio di quello che spera di ottenere Tschira: che i Laureati riescano a trasmettere qualcosa di più di una serie di risultati, un misto di esperienza personale e di visione a volo d’uccello, quel qualcosa che è difficile ottenere a un normale convegno. Alla fine del Forum posso dire con sicurezza che l’obiettivo è centrato in pieno. Riprendo l’aereo per Roma con una piacevole sensazione, turbata soltanto dal ricordo dell’agghiacciante ricostruzione del premio Turing William Kahan di come un errore di programmazione del computer di bordo abbia causato la caduta del volo Airfrance RioParigi.
Materiali didattici
Difficoltà in matematica: la diagnosi di ‘atteggiamento negativo’
Un articolo di Rosetta Zan, del Dipartimento di matematica dell'Università di Pisa e presidente della CIIMUMI, sulla diagnosi dell' "atteggiamento negativo" nei confronti della matematica, che può costituire un punto di partenza per un intervento mirato, invece che la rinuncia a intervenire.
Scena 1:
Azzurra, terza media, deve trovare il perimetro di un rettangolo che ha i lati di 12 cm e 8 cm. Moltiplica 12 per 8. L’insegnante le dice: “Ma perché moltiplichi? Devi trovare il perimetro…” E Azzurra: “…Divido?”
Scena 2:
Nicola, terza liceo scientifico, deve risolvere la disequazione:
Prima scrive:
Quindi:
A questo punto si ferma, e rifiuta di continuare nonostante l’incoraggiamento dell’insegnante.
Questi episodi descrivono due tipi di comportamenti molto frequenti nelle nostre classi: Azzurra sembra rispondere a caso, Nicola addirittura non risponde. Di fronte a tali comportamenti l’insegnante (il ‘bravo’ insegnante) agisce come sempre: corregge, rispiega, fa vedere come si risponde correttamente. Ma lo fa con un certo disagio, avendo la netta percezione che il suo intervento sarà assolutamente inutile. La verità è che il problema, diciamocelo francamente, sta nello studente! È lo studente che ha un atteggiamento negativo verso la matematica, e di fronte a questo non c’è intervento che tenga! La diagnosi di ‘atteggiamento negativo’ in altre parole rappresenta in genere per l’insegnante la presa d’atto del fallimento della sua azione didattica, una dichiarazione d’impotenza, piuttosto che una diagnosi in grado di suggerire una direzione da seguire per mettere in atto un intervento adeguato ai bisogni dell’allievo.Ma è necessariamente così? Oppure la diagnosi di ‘atteggiamento negativo’ può costituire un punto di partenza per un intervento mirato, piuttosto che la rinuncia a intervenire?In realtà di Azzurra e Nicola sappiamo qualcosa di più delle poche informazioni che si possono trarre dalla scarna descrizione data all’inizio. Azzurra è una dei 1600 studenti di cui abbiamo raccolto il tema autobiografico ‘Io e la matematica: il mio rapporto con la matematica, dalle elementari ad oggi’ (Di Martino & Zan, 2010). Racconta così la propria esperienza:“Alle elementari non ero una grossa cima in matematica, quindi in 3a elementare vidi che non ero brava e chiusi così la mia testa, dicendo che questa non faceva per me.”Anche nel caso di Nicola abbiamo altre informazioni: l’episodio che abbiamo descritto avveniva all’interno di un’interazione individuale condotta da una studentessa di un corso di Didattica della Matematica. Ecco uno stralcio di tale interazione, che segue alla rinuncia di procedere da parte di Nicola:I.: Perché invece di ricordarti cosa devi fare, non provi a risolverla da solo?
N.: La matematica è fatta di regole ben precise che vanno seguite, non ci si può inventare nulla. I problemi si risolvono seguendo quelle regole e io, ora, non mi ricordo come si risolvono le disequazioni.Queste informazioni supplementari ci permettono di comprendere meglio i comportamenti apparentemente irrazionali di Nicola e di Azzurra. Dalle parole di Azzurra emerge la convinzione di non potercela fare, cioè uno scarso senso di autoefficacia. Tale convinzione giustifica, nel senso che la rende una scelta 'razionale', la rinuncia a priori a pensare, e quindi il rispondere a caso. Nicola invece esplicita chiaramente le convinzioni che sono alla base del suo comportamento: "Per risolvere disequazioni bisogna applicare delle formule", e "Io non conosco tali formule". E' proprio l’interazione fra queste due convinzioni che da un lato giustifica la rinuncia a provare, dall'altro spiega i primi tentativi di risoluzione, condotti apparentemente a caso. Possiamo dire che Nicola ha una visione della matematica come disciplina fatta da regole fisse da memorizzare e applicare: quella che il ricercatore Skemp (1976) definisce una visione strumentaledella disciplina, contrapposta ad una visione relazionale, secondo la quale la matematica è caratterizzata da relazioni, e l’applicazione di formule prevede la comprensione del perché tali regole funzionano. Anche il comportamento rinunciatario di Nicola ci appare razionale alla luce di questa sua visione, dato che da un lato ritiene di dover ricordare tante regole (una per ogni caso che gli si presenta), dall’altro non si ricorda quella ‘giusta’ per il caso in questione.Come abbiamo visto, le informazioni supplementari che ci permettono di comprendere meglio Azzurra e Nicola sono state ottenute grazie a ulteriori osservazioni, condotte con strumenti inusuali nella pratica scolastica: il tema autobiografico e l’intervista. E proprio dai 1600 temi autobiografici che abbiamo raccolto (Di Martino & Zan, 2010) emerge che l’atteggiamento verso la matematica che uno studente costruisce nel suo percorso scolastico viene descritto utilizzando 3 dimensioni:
la dimensione emozionale (che nei casi negativi va dal semplice ‘non mi piace’ a ‘la odio’) il senso di auto efficacia la visione della disciplina
Questa multidimensionalità dell’atteggiamento fa apparire riduttiva la dicotomia positivo/negativo, e suggerisce piuttosto di considerare ‘profili’ diversi di atteggiamento negativo, a seconda delle dimensioni maggiormente implicate. Ad esempio possiamo dire che il profilo di Azzurra è caratterizzato da un basso senso di autoefficacia, mentre quello di Nicola da una visione distorta della matematica. Alla luce di queste ulteriori osservazioni la diagnosi di atteggiamento negativo comincia ad assumere una connotazione più costruttiva: non più una generica diagnosi che chiude ogni possibilità di recupero, ma un’interpretazione che ci indica una direzione da seguire.Nel caso di Azzurra, l’obiettivo di un intervento di recupero coerente con la diagnosi data sarà quello di sradicare il basso senso di autoefficacia dell’allieva (che viene da ripetute esperienze percepite come fallimentari), convincerla che è in grado di fare matematica. Nel caso di Nicola, bisognerà cercare di sradicare la visione distorta della matematica che ha costruito nel suo percorso scolastico.Naturalmente a questo punto si apre il problema non banale di individuare strategie didattiche adeguate a questi obiettivi: ma questa, come si dice, è un’altra ‘storia’.Rosetta Zan, Dipartimento di Matematica, PisaRiferimenti
1. Di Martino, P., Zan, R. (2010). ‘Me and maths’: towards a definition of attitude grounded on students’ narratives. Journal of Mathematics Teacher Education, 13 (1), 2748.
2. Skemp, R. (1976). Relational understanding and instrumental understanding. Mathematics Teaching, 77, 20–26.
RevolutionineUn racconto di Diego Altobelli. Illustrazione di Emanuele Rosso
In tutta la vita stavi solo aspettandoche questo momento arrivasse
(Blackbird, LennonMcCartney, 1968) «Anche la cassa destra verso il soffitto!», ordinò Giovanni.«Sicuro?»«Te l'ho detto, la punta del triangolo deve essere il lampadario.»Capita a tutti, almeno una volta, di avere il potere di cambiare gli eventi definitivamente. A me è successo il nove agosto del '79, più o meno alle nove di sera, mentre ero seduto al buio ad ascoltare il White Album circondato da candele rosse. Perché vi dico questo? Perché lo so che anche voi avreste bisogno di una rivoluzione ma, di certo, non potete sapere che per ottenerla è sufficiente ascoltare nove volte consecutive la #9 dei Beatles e poi rigirarla.«Nove?», dissi come fosse una stupidaggine.Giovanni fu convincente: «Leggi che c'è scritto» e scandì bene: «Revolution number nine. E noi la ascolteremo nove volte, poi invertiremo il disco e vedremo se ho ragione.»
Dopo gli esami di terza media, con Giovanni avevamo passato più di un mese a raccogliere indizi su un quadernone e a discutere di quello che chiamavamo Il Progetto PID, che stava per Paul Is Dead. Eravamo convinti di poter smascherare il più grande complotto del rock: Paul McCartney era morto in un incidente d'auto ed era stato sostituito da un sosia che aveva ingannato tutti ma, e qui veniva il bello, John Lennon aveva lasciato disseminati nelle canzoni e nelle copertine degli LP piccoli indizi che spiegavano la verità. Qualche esempio?Posizionando uno specchio sulla grancassa, a metà della scritta Lonely Hearths dell'album Sgt Pepper's si poteva leggere chiaramente la data dell'incidente di Paul: il nove novembre del '66. Inoltre, nella foto posteriore di quell'immenso affresco floreale, Paul era molto più alto e robusto degli altri ed era l'unico inquadrato di spalle.«Si vede che non è lui.»E, se non bastasse, sul distintivo della sua giacca, c'era uno stemma con impresse le lettere OPD.
«Officially Pronounced Dead.»«E che vuol dire?»«Ufficialmente Dichiarato Morto.»«Pensa te, e io che credevo fosse il distintivo della Polizia...»E questo non era ancora niente se paragonato alla foto di Abbey Road, «L'ultimo album prima dello scioglimento definitivo». Lì John, Ringo, Paul e George sono fotografati mentre attraversano le strisce pedonali. Abbey Road non è una strada qualsiasi perché si trova di fronte agli studios dove i Beatles registrarono tutte le loro canzoni.«Ti rendi conto? Non stanno "attraversando", stanno "uscendo dagli" studios. Per non tornarci più.»Guardando attentamente l'immagine si capiva subito che qualcosa non andava e quel qualcosa era, cito a memoria dal nostro quadernone:UNO: John vestito di bianco (come un sacerdote) seguito dagli altri tre (come in un corteo funebre),DUE: l'insolito aspetto di Paul: scalzo, con gli occhi chiusi e la sigaretta nella mano destra (dettaglio singolare se si pensa che era mancino), e poiTRE: la targa dell'auto parcheggiata dietro. Si leggeva chiaramente 28IF e quello era, ovviamente, un messaggio di John: 28 sarebbe stata, infatti, l'età di Paul "se" fosse stato ancora vivo al momento dell'uscita di (nonché da) Abbey Road. Insomma, altro che Yoko Ono, altro che rivalità e carriere soliste... Era solo questione di tempo e con Giovanni avremmo dimostrato il vero motivo per cui si erano sciolti i Beatles.«Moriremo asfissiati.»«Non si muore asfissiati con le candele.»«Forse perché queste si accendono quando uno è già morto.»«Cos'è? Ora che ci siamo hai paura?»«Figurati se mi fanno paura nove ceri rossi.»«Allora passami il disco...»La madre di Giovanni entrò senza bussare e si precipitò verso la finestra spalancandola: «Ma non vi vergognate?»La madre di Giovanni era sempre nervosa, ma quel pomeriggio lo era più del solito. Nella stanza di sopra si consumava l'ultimo atto di una tragedia che andava avanti ormai da troppo tempo: il vecchio nonno stava morendo. Per il medico ogni giorno poteva essere l'ultimo. Addirittura ogni ora. I figli aspettavano la notizia solo per l'eredità e la mamma di Giovanni era vicina all'esaurimento perché non poteva annunciare il triste evento.«Se sento solo un rumore è meglio che non vi fate trovare qua dentro.»Non ci facemmo intimidire e richiudemmo la finestra. Stavamo per ascoltare Revolution #9, la penultima canzone del secondo LP del White Album. Quella con la voce che ripeteva "number nine" e, al contrario, "turn me on dead man" cioè, letteralmente, una cosa tipo “eccitami uomo morto”.Nessuno sapeva cosa significasse, tranne Giovanni, che mi avrebbe spiegato tutto dopo l'esperimento con il giradischi e le candele.«Tempo?», chiese Giovanni con la puntina dello stereo pronta sul disco e la faccia in penombra.«Nove per nove 81, un'ora e ventuno minuti», risposi con il quadernone aperto e la matita in mano.«Perfetto. Se i miei calcoli sono esatti finiremo esattamente alle nove e nove minuti.»«81 minuti: 8 + 1 = 9, il nostro numero difettivo preferito.»«E non solo il nostro...»«Perché?»«Nove è il numero del diavolo.»«Guarda che sei è il numero del diavolo.»«Esatto: 666 cioè 6 + 6 + 6. Cioè 18 e quindi 8 + 1»«...»Scrissi un po' preoccupato: «Revolution #9. Primo ascolto.»Tutti i non esperti commettono l'errore di confondere Revolution #1 con Revolution #9.La prima è quella con John che canta “dici che vuoi la rivoluzione? Beh sai, tutti noi vogliamo cambiare il mondo”. Pura poesia, anche se noi preferivamo la versione più veloce e graffiante suHey Jude, quella dove Paul urla e John è più incazzato del solito. Revolution #9, invece, è un pezzo strumentale di 9 minuti. Era molto importante per il Progetto PID anzi, un vero punto di non ritorno tanto da convincere Giovanni che, se ascoltato al contrario, avrebbe potuto sprigionare potenti campi magnetici.«Schhh... inizia!»
Mi concentrai e scrissi ciò che ascoltai: il suono gracchiante del vinile, una conversazione incomprensibile, una melodia al pianoforte che si sviluppava intorno a un mi minore e poi una voce da speaker che ripeteva “number nine, number nine, number nine”. Scrutai il viso attento di Giovanni. La #9 proseguì con sette lunghi minuti di rumori. Riconobbi grida e frammenti di musica orchestrale. Poi un clacson e una frenata.«Hai sentito?», sorrise Giovanni: «John ci ha descritto l'incidente di Paul!»Era felice come se mi avesse appena comunicato il codice per decifrare la Stele di Rosetta. Annuii serio e continuai a prendere appunti nel semibuio lugubre della stanza. Il pezzo arrivò alla fine e iniziò Good Night, l'ultima traccia: una ninna nanna di John cantata da Ringo, ininfluente sia per ilPID che per la discografia dei Beatles.Giovanni spostò delicatamente la puntina e la #9 ripartì con la conversazione, il piano in mi minore, e number nine.La storia della morte di McCartney non mi aveva mai convinto: secondo me Paul e gli altri si erano divertiti un casino a inventare falsi indizi per alimentare la leggenda. Giovanni però vedeva una cospirazione di proporzioni cosmiche e, ogni volta che arrivavamo a questo punto della discussione, riapriva il quadernone del Progetto PID e mi mostrava le foto di Sgt. Pepper's con la scritta Lonely Hearths e Abbey Road con la targa 28IF, nonché le dettagliate schede dei testi di tutte le canzoni contenenti doppi o tripli significati che avevamo scovato ascoltando i dischi usciti dopo l'incidente di Paul. Poteva andare avanti per ore e, alla fine, accettavo sempre la sua teoria più per sfinimento che per convinzione.La traccia finì e ripartì: «Altri 63 minuti e ascolteremo number nine al contrario!»«Sicuro di volerla ascoltare nove volte?»«Sì.»«Perché non facciamo una pausa?»«Impossibile.»«Mi manca l'aria. Moriremo asfissiati e al buio.»«Non moriremo. E tu mi ringrazierai per averti fatto saltare pianoforte.»«Se i miei lo scoprono mi mettono in punizione per un mese.»«Meglio, così lasci perdere il piano e ti compri una Fender, come quella di John.»«Revolution #9: terzo ascolto.»Capii solo quel pomeriggio cos'era che mi faceva così paura del White Album.Non il fatto che fosse il disco numero nove dei Beatles. Sì, lo so che in realtà era il decimo ma in questo appoggiavo in pieno Giovanni perché neanche io credevo che i primi due potessero essere considerati separatamente, e non per la vicinanza di pubblicazione no, ma semplicemente per il fatto che le canzoni scritte da LennonMcCartney erano così poche da non riempirne nemmeno uno di disco. Non era, dunque la presenza del numero nove che tanto eccitava Giovanni a spaventarmi.«E sai di quante lettere è composto il cognome di Paul?»«...»«Esatto.»E neppure tutte le corrispondenze trovate nelle canzoni che sembravano portarci dritti dritti alla#9, come John che sussurrava "Paul è l'uomo morto: mi manca..."«Revolution #9: quarto ascolto.»E, visto che ci siamo, non era nemmeno la vecchia storia del serial killer che aveva fatto violentare e uccidere famosi ricconi di Hollywood scrivendo sui muri con il loro sangue i titoli di un paio di canzoni del White Album (per dovere di cronaca: Piggies e Helter Skelter). Quel nano strabico e semianalfabeta ci aveva solo fatto incazzare di brutto. Come si era permesso di infangare con i suoi psicopatici deliri di onnipotenza la nostra band preferita?«Revolution #9: quinto ascolto.»No, a terrorizzarmi era un elemento all'apparenza innocuo e senza alcuna importanza: il fatto che ilWhiteAlbum fosse completamente bianco. Giovanni credeva di conoscere anche il motivo della mia inquietudinecromatica: «Per gli indiani, il bianco è il colore del lutto, della morte e dei fantasmi e, pensaci bene:quando hanno pubblicato il disco?»«Dopo essere tornati dal viaggio di meditazione in India?»«Già.»Niente sembrava casuale.«È normale che tutto quel bianco terrorizzi.»
Ma non era solo quello.Il bianco accecante, l'assenza totale di qualsiasi elemento grafico a cui appigliarmi destabilizzava e minava le certezze conquistate con tanta fatica in più di un mese di lavoro sul Progetto PID: «E se John ci stesse dicendo che gli indizi non sono mai esistiti? Che non c'è mai stato nulla da trovare?»«E se invece ci stesse invitando ad andare oltre la superficie e a cercare all'interno del disco?»Certo, in quel caldo pomeriggio del '79, al buio della sua cameretta, nemmeno la sofisticata e iperbolica cabala di Giovanni sarebbe arrivata a concepire che, l'anno successivo, un altro schizzato con in tasca Il Giovane Holden di Salinger avrebbe ucciso John sotto il portone di casa.Il Giovane Holden.L'unico libro dalla copertina totalmente bianca.«Ok ripartiamo: Revolution #9: sesto ascolto.»Secondo Giovanni, con la #9 i Beatles avevano provato a riportare in vita Paul ma non c'erano riusciti. Luiinvece aveva capito come fare: «Si deve ascoltare nove volte la traccia prima di far girare il disco alcontrario. Solo allora la preghiera della canzone diventa efficace!»«Number nine è una preghiera?»«Certo.»Non capivo: «Ma efficace per cosa?»Appoggiò la puntina con precisione millimetrica: «Per resuscitare i morti».«Revolution #9: settimo ascolto.»Secondo la lettura di Giovanni “eccitami uomo morto”, cioè "number nine" ascoltata al contrario, non era da intendersi come una metafora sessuale ma un canto di gioia per una avvenuta resurrezione. "Turn me on dead man" era John che diceva a Paul: «Ehi amico, torna e rendimi felice...»«Che vuoi fare, riportare in vita il vero Paul McCartney?», chiesi ipnotizzato dai rumori orchestrali della #9.«Che stupidaggine, e come potrei? Faremo solo un esperimento per capire se funziona.»La #9 finì.«Cambio!»Giovanni venne a sedersi al mio posto e prese il quadernone mentre io andai al giradischi.«Revolution #9: ottavo ascolto.»La traccia procedette lenta. Ormai conoscevo a memoria tutti i passaggi: il piano, number nine, l'orchestra, il clacson, la frenata. Vicino allo stereo vedevo la puntina consumare i solchi del disco e i suoni materializzarsi in una sorta di pseudoquadrifonia ottenuta grazie all'ingegnosa collocazione delle casse a 90 gradi verso il lampadario. Le note ci avvolgevano completamente insieme alla fuliggine cancerogena dei ceri e i minuti successivi passarono così, senza troppi pensieri finché non arrivammo al termine dell'ultimo ascolto: il nono.«Adesso scopriremo se la nostra teoria è esatta!»Mi feci coraggio e, su ordine di Giovanni, invertii il verso di rotazione del piatto e alzai il volume al massimo. Guardai la puntina scendere lentamente per l'ultima volta e chiusi gli occhi pensando a Claudia per evitare di scappare da quella stanza soffocante. Amavo Claudia ed ero sicuro che se fossi sopravvissuto alla #9 sarei riuscito certamente a baciarla. La puntina toccò delicatamente il disco. Il suono che si sprigionò era talmente forte da penetrarmi direttamente nel cervello: una strana onda sincopata che andava dalla cassa destra a quella sinistra fece tremare le pareti. I toni baritonali mi spaventarono. Sembravano voci cupe di spie del KGB. Poi "turn me on dead man"ripetuto tre volte con un forte accento al centro del pentasillabo: «turmeòndeadman turmeòndeadman turmeòndeadman», un accecante lampo di luce bianca e un fragore di vetri rotti e, dopo, buio e silenzio.Secondi che durarono l'infinito.Giovanni si avvicinò con un cero e vedemmo il disco che girava muto.«Cazzo.»Il lampadario era esploso lasciando un alone nero gigante. Giovanni non fece nemmeno in tempo a dire «Funziona!» che la madre irruppe sbraitando. Ricordo solo le schegge di vinile dalle forme irregolari che dalla testa di Giovanni si schiantavano sul muro e la mia corsa senza fiato per le scale e poi per strada con il White Album ancora caldo stretto al petto.Più tardi seppi da un vicino che la madre non solo aveva strappato il quadernone del Progetto PIDe aveva proibito a Giovanni di usare il giradischi per tutta l'estate ma che, nel suo impeto distruttivo, aveva frantumato Sgt. Pepper's e Abbey Road e, non ancora pienamente soddisfatta, l'album rosso e quello blu, che era la mia raccolta preferita in assoluto.
Quella sera mia madre parlava al telefono sottovoce. Diceva che il nonno di Giovanni si era alzato dal letto e se n'era uscito di casa bestemmiando. Diceva che tutti erano rimasti sconvolti: «Un miracolo!» Diceva che la mamma di Giovanni non la smetteva più di piangere: «Sempre sia lodato.»Comunque, l'estate finì prima che avessi trovato il modo di baciare Claudia e a settembre iniziai il liceo dimenticando tutto, distratto com'ero dai leggings delle ragazze più grandi e da una nuova passione: il punk. Il mio nuovo pantheon si riempì di divinità perverse sulle quali regnava indiscusso Joe Strummer insieme ai suoi Clash e, per quel che mi riguardava, chiusi il pianoforte, strappai i jeans e imparai a suonare una Strato bianca abbracciando una nuova filosofia riassumibile nell'assioma «'fanculo tutto!» e se ve lo state chiedendo sì, è vero, il vecchio Paul non è mai morto ma voglio dirvi una cosa: l'uomo sulle copertine dal '66 in poi non è lui. Per un'estate credemmo che l'avessero rimpiazzato nella band, mentre invece la verità era che avevano fotografato un sosia, un doppione. Aveva ragione Giovanni: «Quello sui dischi è un impostore.»FINEL'autore ci tiene a precisare che la splendida illustrazione a corredo della storia, strettamente autobiografica, è stata realizzata da Emanuele Rosso, già autore di Passato, Prossimo (Tunué Editore). Per visualizzare l'illustrazione a tutto schermo è sufficiente cliccare sull'immagine oseguire il link.Dell'autore di Revolutionine invece, se interessa, sempre su Maddmaths! è possibile leggere Viaggi nel tempo, istruzioni per l'uso e Il giorno in cui viaggiammo più veloci della luce (gli alieni parlarono in francese e ci dissero scemi)© Diego Altobelli | www.revolutionine.comRaccontino rilasciato sotto licenza Creative Commons AttributionNonCommercialNoDerivs 2.5
Perché l’ho fatto? Leo Ortolani ci racconta perché ha scritto Misterius
Continuando a fare le cose di sempre sarebbe portato in trionfo dai lettori. Che cosa spinge un fumettista come Leo Ortolani a confrontarsi con gli interrogativi della Scienza? Probabilmente non lo sapremo mai ma gli abbiamo chiesto perché ha fatto MISTERIUS – Speciale Scienza. E sapete cos’ha risposto? Scopriamolo insieme. (L'intervista e il glossario sono a cura di Roberto Natalini, con la collaborazione di Andrea Plazzi e l'amichevole aiuto di Amedeo Balbi, e sono apparsi per la prima volta in "Comics & Science", a cura di Roberto Natalini e Andrea Plazzi, Edizioni CNR, ottobre 2013). NdR.: Gli asterischi nel seguito rimandano ad altrettante note nel Glossario che trovate in fondo alla pagina.
Sei laureato in Geologia: viene prima quella o RatMan? Eri un ragazzino che andava a letto con la sua collezione di minerali e che a un certo punto si è messo a fare il fumettista, o avevi già deciso che volevi disegnare le storie del Ratto e per passare il tempo ti sei iscritto all’università? Perché proprio geologia?
Viene prima RatMan. Anzi, il fumetto in generale. Ho sempre amato i fumetti, ho sempre fatto i fumetti. Ma mia madre, che è pittrice e la sa lunga sul destino di chi segue l’arte, mi disse “Fai quel che vuoi, ma preparati un piano di fuga che funzioni”. Non disse proprio così, ma quasi. Mi consigliò, insomma, di prendere una laurea, di specializzarmi in qualcosa, di avere un mestiere normale, che quando dici alla gente cosa fai per vivere, la gente riesca a capirlo. Così, arrivato in quinta liceo, presi il libretto con tutte le facoltà che c’erano a Parma e mi misi a scegliere quella che avrei potuto fare. La scelsi per esclusione. E perché c’era quella frase, nella presentazione della facoltà, che mi sembrava bella... qualcosa che suonava tipo “studiando geologia, vi accorgerete di abbracciare una diversa percezione del tempo, misurato in milioni e milioni di anni. E vi sentirete delle inutili merdacce”. La seconda parte l’ho aggiunta io, ma il senso era quello.
Ti senti un nerd? Guardavi “Star Trek” o “Happy Days”? Se hai guardato tutti gli episodi di “Ai confini della realtà” sei un nerd, anche se in camera avevi il poster di Fonzie.
Mi sento abbastanza nerd. Ma è inevitabile per chi vive in un mondo di fantasia. Ovviamente guardavo “Star Trek”, e anche Fonzie. Ma non era lui il mio modello. Io ero più come Richie. O Potsie. O Marion Cunningham.
Cosa hai pensato quando Andrea Plazzi ha cominciato a parlarti di “scienza e fumetti”? Hai cambiato discorso o sei corso subito a guardare su Wikipedia?
Quando ha iniziato a parlare di scienza, sono stato salvato da Greta, la Scimmia che batte i piatti. È una simpatica invenzione del cervello umano che lo preserva da conversazioni troppo impegnative da seguire. Inspiegabilmente, Greta mi si attiva anche a Messa, alla lettura del Vangelo: il celebrante inizia con “dal Vangelo secondo Giovanni...” e appare Greta. Quando se ne va, siamo già al Credo. Non so perché. Ma ce lo spiegherà Misterius.
Mai del tutto tranquillo, Leo Ortolani tra due matematici, Roberto Natalini e Andrea Plazzi. Dietroocchieggia Stefano Pisani.
Hai dichiarato che a scuola sei sempre stato terrorizzato dalla matematica. Durante la preparazione di Misterius, che cos’hai provato incontrandoti in un umido seminterrato con un nutrito gruppo di matematici, fisici e altri scienziati assortiti?
Per un attimo, quando ci siamo trovati là sotto, e io ero con le spalle al muro senza vie di fuga, mi è apparso il volto di mia madre che scuoteva la testa in segno di disappunto. Gli scienziati continuavano ad arrivare, sempre più numerosi. E se all’inizio avrei ancora potuto aggirare facilmente Amedeo Balbi, dopo pochi minuti la densità di conoscenza era tale che non avrei potuto attraversarla nemmeno con un’ignoranza a punta come la mia. Per fortuna si sono dimostrati amichevoli, ci siamo presentati, si sono detti disposti a raccontarmi quello che stavano facendo e allora ci siamo seduti e ha iniziato un matematico a parlarmi di cosa mettere nello zaino[*]. A quel punto è uscita Greta. Quando ha finito di battere i piatti ero già sul treno di ritorno per Parma.
L’inizio della tua storia è folgorante e forse addirittura un po’ troppo veloce. Per esempio, non ho capito proprio come tu sia riuscito a far calcolare alla Macchina di Turing il numero di telefono di Monica Bellucci. A me esce sempre il cellulare di Plazzi. Dove sbaglio?
Probabilmente non hai inserito correttamente le misure della Bellucci. La Macchina di Turing[*] le legge e le somma sul nastro, per questo esce il numero di cellulare di Plazzi.
In questi mesi hai studiato, hai parlato con molti scienziati e simili amenità. Quale idea ti sei fatto sulla matematica come disciplina? Quali direzioni credi che possa seguire la ricerca e che cosa diresti ai giovani che volessero intraprendere la carriera accademica in questa disciplina?
Solo quello che disse Gandalf: “Fuggite, sciocchi!”. Peraltro lo disse anche a chi voleva fare geologia. Ma avevo le cuffie del walkman.
Per Misterius hai dovuto lavorare duro. Per esempio, sul tuo blog una volta hai iniziato un post con questa frase che mi ha fatto saltare sulla sedia: “Mentre son qui nel fornetto scaldavivande di Parma a guardarmi dei gran video sull’ipotesi di Riemann...” Anche se sono un matematico, quello non è
proprio il mio campo (un po’ come se a te chiedessero di parlare del fumetto esistenzialista francese degli anni Cinquanta), per cui ti dispiacerebbe spiegarmi di che cosa parla questa ipotesi? Hai fatto progressi verso la sua risoluzione? Non è che hai qualche idea da passarmi?
Ah, i bei momenti in cui mi fanno una domanda a cui non so rispondere! Del video sull’ipotesi di Riemann[*] ricordo solo questo tipo che fa il Misterius della situazione e alla fine entra in un mondo astratto dove ci sono delle figure tridimensionali fatte a monti e valli, e dove ci sono le valli e la funzione si annulla (o almeno credo), ci sarebbero i numeri primi. E se si va avanti all’infinito, sono tutti su una linea. Cosa questo voglia dire, lo ignoro. Ma probabilmente era un modo come un altro per Riemann di passare tutto il giorno in studio e lasciare alla moglie il compito di fare la spesa, andare a prendere i figli a scuola, seguirli nei compiti, preparare la cena. Poi alle sette e mezza, Riemann rientrava a casa e fingeva spossatezza: “Ho trovato un altro numero primo! Non ti dico la fatica!” E invece era uscito a bere con l’amico Gunther.
Ricordiamo che l’Istituto Clay ha messo in palio sette premi da un milione di dollari per la soluzione di altrettanti problemi matematici, i cosiddetti “Problemi del Millennio”[*]. A parte l’ipotesi di Riemann, hai qualche suggerimento su quale problema ti sembra più risolvibile?
Ma certo.Quello più facile, che ho peraltro già risolto, è quello in cui ci si domanda se NP = P[*].Ovviamente no! Ma lo vedo solo io? C’è una “N” in più! Ah! Ah! Ah! Matematici!Dove ritiro il milione?
Anche se in modo abbastanza velato, fai capire chiaramente che secondo te la maggior parte delle persone odia la matematica e ne ha paura. Ne sei certo? Perché mai dovrebbe?
Cosa posso rispondere a un matematico? Posso fidarmi? E se poi mi dai quattro? Anni e anni di campo di concentramento scientifico non possono essere cancellati così. Come se fossero scritti sulla lavagna. Noi della sezione E, oltretutto, siamo stati terrorizzati dal primo robot vivente. Controllava ogni nostra parola, durante l’interrogazione e se ne usavamo una diversa eravamo finiti. Un giorno, un mio amico il cui padre era professore universitario di fisica, risolse un problema matematico con un approccio diverso, suggeritogli dal padre. Un approccio che il robot non ci aveva insegnato. E questo lo mise in difficoltà. E ai robot non piace essere messi in difficoltà. Un giorno, consegnandomi un compito in classe mi disse: “Sai, Ortolani, con questi errori mi meraviglia che tu sia ancora a piede libero”.Era un personaggio.Il Darth Vader della matematica.Compagne di classe che piangevano alla lavagna. E il robot le apostrofava senza pietà: “Signorina, se piange per una cosa così, cosa farà quando le morirà qualcuno?” Questa era la matematica, per noi. La paura. E nelle altre classi non andava meglio. L’unica volta che ho amato la matematica è stato alle medie. Perché la mente riusciva a trovare il modo di risolvere le cose. Mi divertiva. Ma dalla terza liceo in poi... dagli studi di funzione in poi... nulla ha avuto più senso.Solo una volta, studiando le funzioni nello spazio, arrivai per un attimo a una sorta di illuminazione. Capii la soluzione di un problema... era bellissimo, come se mi fossi trascinato oltre un muro e riuscissi a vedere quello che mi nascondeva. è durato un attimo, poi quando ho cercato di spiegarlo ai miei amici, sono scivolato di nuovo, rovinosamente giù dal muro, nella fossa dell’ignoranza.
Il matematico della tua storia si distingue per la pettinatura eccentrica, le intuizioni fulminanti, la scarsa comprensione da parte dei colleghi. Come sei venuto a conoscenza della straordinaria biografia di JeanPierre Bagolot?
Ho trovato un testo di Bagolot nella biblioteca comunale di Guastalla (RE). Era tra Il tortello di zucca mantovano e Le montagne del Trentino: come evitarle.
E se dovessi fare un confronto tra Cédric Villani e JeanPierre Bagolot?
L’indubbio elemento di forza di Villani è che si diverte. E quando uno si diverte è perché ha il controllo
della materia. Ma per raggiungere il controllo devi divertirti. Bagolot, a differenza di Villani, si divertiva a guardare gli altri. E poi li imitava. Oppure trovava soluzioni particolari a problemi che poi non era in grado di affrontare. Ma il problema vero è che secondo me non si è mai divertito veramente.Forse solo una volta. Quando ha fatto lo scherzo del sacchetto di carta con dentro la cacca che lo metti davanti alla porta di un collega, bussi e intanto dai fuoco al sacchetto, il collega esce e vede il sacchetto che brucia e lo pesta per spegnere le fiamme. Fu dopo quell’episodio che Fermi[*] lasciò Gottinga.
Dimostrando i suoi famosi teoremi di incompletezza, Kurt Gödel[*] precede di poco il nostro sfortunato amico. Ho ammirato la precisione con cui hai esposto il profondo risultato di Gödel, e soprattutto l’impeccabile ortografia dei puntini sulla “o”. Sapresti ridirlo con parole tue? Vedi una connessione con la Macchina di Turing?
So dirlo con le parole di Wikipedia. Per dirlo con le mie, “Io non dico mai la verità”. E poi lascerei la gente a divertirsi cercando di interpretarla.Una volta l’ho detto in macchina con Turing. Lui ha accostato e mi ha fatto scendere.Gli ho tirato una mela.
In realtà, come fai giustamente osservare, un punto di contatto tra Bagolot e Villani esiste ed è il problema detto dello “Smorzamento di Landau”[*]. Entrambi hanno affrontato con efficacia il problema e la soluzione di Bagolot è la più semplice. Perché allora gli sono mancati i dovuti riconoscimenti? Non ti sembra un’iniqua emarginazione?
Sono d’accordo. Oltretutto, dopo quella puntata di Misterius, in casa nostra abbiamo iniziato a usare lo smorzamento di Landau quando mia figlia Lucy Maria dà in escandescenze. In casi del genere, l’unica soluzione adeguata è quella di Bagolot. Tuttavia, Lucy Maria non sa chi sia Landau, e persevera. Il cammino della matematica è costellato anche di insuccessi.
E parliamo del frazzo, che a me sembra una scoperta sensazionale. Certo non da meno dell’analisi nonstandard[*] e dei numeri iperreali di Abraham Robinson, del GrossOne[*] di Yaroslav D. Sergeyev e di altre estensioni dei numeri ordinari. Un concetto molto “fuzzy” e dalle interessanti possibilità applicative. Non sarebbe ora di cambiare i vecchi e ammuffiti programmi ministeriali e introdurre nelle scuole queste nuove idee?
Io il frazzo l’introdurrei fin dalle elementari. Che i bimbi imparino subito a entrare in confidenza con questo nuovo, entusiasmante numero. Oltretutto, molte volte i docenti potrebbero uscire dall’ambiguità delle votazioni. Invece di dare “sei più” o “sette meno meno”, possono dare “frazzo”, che è molto più chiaro.
E poi irrompe in scena Villani, anche se subito viene preso da altri problemi. Cosa pensi delle sue ricerche? Che legame credi che abbiano col suo modo di vestire?
Credo che Gauss gli abbia passato un vecchio catalogo della Vestro, spacciandoglielo per l’ultima moda francese in fatto di matematici.Uno scherzo che il professor Villani, impegnato nelle sue ricerche, non ha colto. Ora, dopo tanto tempo, sembra scortese farglielo notare. Delle sue ricerche so ovviamente pochissimo, ma conto di leggere il suo libro, Il teorema vivente, non tanto per capire cosa ha fatto, nel campo della matematica, quanto per sapere come lo ha fatto, dovendo anche vivere.
Il Sovrintendente Plazzus mi fa capire che è tempo che mi occupi di fisica, altrimenti mi rimpiazza con Balbi. Io però di fisica ci capisco poco. Ma proviamo. Secondo te, perché la teoria delle stringhe[*] è in una crisi così profonda, tanto che secondo alcuni sarebbe completamente superata?
Colpa del film “Star Trek: Generations”, in cui Kirk viene eliminato dall’universo di Star Trek con quella soluzione fastidiosa e sciocca in cui precipita in un canyon come Wile E. Coyote. Da quel momento, tutto ciò che ha a che fare con quel film, compresa, appunto, la stringa che permette di far convivere Picard e Kirk nello stesso momento, è stato messo al bando.
Lasciando perdere per un attimo il problema della materia oscura[*], come spieghi la presenza dell’energia oscura? Sei d’accordo con Leveraine? Basta che non chiediamo a Balbi, per favore.
Sono assolutamente d’accordo con Leveraine, e spezzerei oltretutto una lancia a favore del fratello maggiore dell’universo. Nel momento in cui l’universo deve alzarsi, e l’energia oscura lo sollecita, non si è mai accennato alla presenza, nella stessa camera, del fratello maggiore dell’universo, che chiamaremo “universitario”, il quale poteva alzarsi anche un’ora dopo, ma ogni mattina veniva accelerato insieme al fratello. Un’ingiustizia che solo Leveraine ha trattato nell’articolo “Mi girano le galassie”.
Parli della scienza come di un “rifugio sicuro per tutti gli uomini magrolini e con gli occhiali”. Quindi secondo te chi fa scienza lo fa perché altrove è stato scacciato da uomini nerboruti che ci vedono benissimo?
È la mia teoria sul bullismo. Più aumenta il livello degli studi, più diminuiscono i bulli. Questo vorrebbe dire che i bulli sono tonti? Sì. E lo dico con tranquillità, tanto i bulli non arriverebbero mai a leggere un’intervista così fino in fondo. I peggiori non la leggono nemmeno, la prendono a calci.
Un’altra affermazione che fa riflettere: “Scienza: spiegare come funziona il mondo che ci circonda in maniera che gli altri non possano capire”. Ma è proprio vero che gli scienziati ci tengono a non farsi capire?
Ma certo, è la naturale conseguenza della mia teoria. Se gli scienziati spiegassero le cose in modo chiaro e accessibile a tutti, chiunque potrebbe arrivare al loro livello e si troverebbero ancora davanti i bulli delle scuole dell’obbligo. In questo modo, la barriera culturale tiene.
Con tutto il lavoro preparatorio che hai fatto, il tuo livello di confidenza con fisica e matematica è al massimo. Si sente che sei in gran forma. Prova a immaginare una cosa difficile: come parleresti di matematica e fisica a dei liceali? Cosa diresti? Come glielo diresti (nell’ipotesi che in classe non ci siano tizi nerboruti dalla vista eccellente)?
Non ci proverei nemmeno, essendo incapace di trasmettere qualunque tipo di sapere, ho anche un foglio del medico curante che lo certifica. Darei un bel compito in classe e poi mi metterei a leggere Playboy.
Ora una domanda di importanza capitale che apre le porte alla ricorsività. La famiglia Chiapparotta è la tipica famiglia media italiana che non legge e guarda sempre la TV. Ma per caso, non è che stava guardando Misterius (e il cerchio si chiude)?
No, i Chiapparotta guardano di solito i programmi con quelli che cantano e gli altri che li giudicano. O quelli dove c’è lei che fa la corte a lui, seduto sul trono, uno che si vede che era un bullo, perché ha il viso disteso, la pelle fresca e un bel vestito, tutti indizi di scarsa attitudine allo studio.Ma se proprio cercate un qualche punto di contatto tra il narrato e il narratore, io sono quello che guardava gli organi sessuali sull’enciclopedia, deluso perché erano in sezione.In questo modo il mio interesse verso il sesso è diminuito, lasciando spazio a quello per lo studio, fino a quando, al quarto anno di geologia, ho scoperto che le studentesse non ce l’avevano disegnata. Ma avrei dovuto arrivarci per similitudine, visto che nemmeno il mio era disegnato e in sezione.Ma credevo di avere una malattia.E' stato allora che ho cominciato a seguire MISTERIUS, per non trovarmi più in difficoltà nei confronti del Sapere.
Secondo te “del Sapere” fanno parte anche argomenti controversi come i Templari e le scie chimiche?Su questo non ho dubbi: per quanto mi riguarda, le uniche scie chimiche importanti sono quelle rilasciate dai Templari.Diffidate delle altre.
Che ne pensi delle trasmissioni televisive che parlano di scienza? Ne hai una preferita?Ho smesso di guardare la televisione sei anni fa. Dopo una puntata di “Voyager”.
GLOSSARIOAnalisi nonstandard, numeri iperrealiRiformulazione dell’analisi matematica proposta negli anni Sessanta dal matematico di origine polacca Abraham Robinson, con lo scopo di permettere un uso rigoroso dei più intuitivi “infinitesimi” proposti da Gottfried Wilhelm Leibniz. Robinson definisce gli infinitesimi come numeri positivi “più piccoli di qualsiasi numero razionale dato” ed estende in questo modo i tradizionali numeri reali agli “iperreali”, definiti come la somma di un reale e di un infinitesimo.Bagno chiuso (Teorema del)Per ora non è ancora stato dimostrato ma in compenso esiste quello “del grafico chiuso”. Secondo questo teorema, un operatore (cioè una funzione) lineare tra due spazi vettoriali “normati completi”, in cui è cioè definita una nozione generalizzata di lunghezza, è continuo se e soltanto se il suo grafico è un insieme chiuso (il grafico di una funzione f tra gli insiemi X e Y è l’insieme delle coppie (x, f(x)), per tutti i possibili elementi x di X).Fermi, Enrico (e Gottinga)Nel 1923 la città tedesca era la capitale mondiale della ricerca fisica e matematica. Il grande fisico italiano vi giunse accompagnato dalla fama meritatissima di enfant prodige, attirato dalla presenza di grandi nomi come Max Born, Werner Heisenberg, Wolfgang Pauli e Pascual Jordan. Là lavorò alle teorie di Paul Ehrenfest, trascorrendovi effettivamente un semestre di studio intenso, che trovò però insoddisfacente. Ora sappiamo perché.Galois (Problema inverso di)Studiato da oltre un secolo ma ancora non completamente risolto, questo problema può essere formulato così: fissato un campo F, quali gruppi sono gruppi di Galois di una qualche estensione di F? È detto “inverso” perché di solito, data un’estensione di un campo, si cerca di determinarne il gruppo di Galois.All’inizio dell’Ottocento il matematico Evariste Galois elaborò un metodo generale per stabilire se un’equazione algebrica ammette o meno radici calcolabili con operazioni elementari. Il suo lavoro è considerato l’atto di nascita della moderna teoria dei gruppi. Morì a soli vent’anni in un duello.GrossOneIl matematico russo Yaroslav D. Sergeyev, residente da anni in Italia, ha proposto una nuova unità di misura per l’infinito, il “GrossOne”, che permette di maneggiare computazionalmente e in modo rigoroso i concetti di infinito e infinitesimo.Millennio (Problemi del)Sono sette problemi matematici proposti nel 2000 dall’Istituto Clay: la risoluzione di ciascuno di essi frutterebbe al vincitore un milione di dollari. Per ora è stato risolto solo uno dei problemi, a opera del matematico russo Grigori Perelman, che nel 2006 ha dimostrato la verità della congettura di Poincaré (per questo gli è stata conferita la Medaglia Fields, che Perelman ha però rifiutato). I restanti problemi sono: “P=NP?”, la Congettura di Hodge, l’ipotesi di Riemann, la congettura di Birch e SwinnertonDyer, la teoria quantistica di YangMills, la risoluzione delle equazioni di NavierStokes.Oscura (materia, energia)“Materia oscura” è un termine usato in cosmologia per indicare la materia dell’Universo che non è direttamente osservabile, se non per i suoi effetti gravitazionali. Tranne che per questi ultimi, la sua natura e le sue caratteristiche sono quindi sconosciute. Dovrebbe formare circa un terzo del contenuto totale dell’universo e l’85% della materia. Non va confusa con l’energia oscura, che è un’energia prevista dalla Relatività Generale di Einstein e che spiegherebbe l’apparente espansione accelerata dell’Universo.Stringhe (Teoria delle)Si tratta di una teoria fisica il cui obiettivo è quello di spiegare le leggi dell’universo combinando il Modello Standard delle particelle e la Teoria della Gravitazione. Al posto delle particelle puntuali della fisica tradizionale, si considerano oggetti unidimensionali detti “stringhe”.Una delle estensioni della “teoria classica delle stringhe” è detta “teoria M” e prevede l’esistenza di 11 dimensioni (il tempo, più 10 spaziali).
La critica principale che viene normalmente mossa alla teoria delle stringhe (e alla teoria M) è la mancanza di evidenze sperimentali e il loro scarso potere predittivo.Zaino (Problema dello)Supponiamo di avere uno zaino che può sopportare al massimo un certo peso, e un certo numero di oggetti, ciascuno dei quali dotato di un peso e di un valore. Si tratta di riempire lo zaino col massimo valore complessivo possibile senza superare il peso massimo consentito. È un problema che ricade nell’ambito della cosiddetta Ricerca Operativa, e trova applicazione in ambiti come l’ottimizzazione dei portafogli finanziari, la produzione industriale, la criptografia. La complessità del problema può crescere enormemente all’aumentare degli oggetti. Più precisamente, si tratta di un problema NPdifficile, cioè con una difficoltà di risoluzione che è almeno quella di un problema NPcompleto (v. “P=NP?”).








































































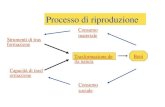



![LA TRASFORMAZIONE [modalità compatibilità]](https://static.fdocumenti.com/doc/165x107/5870b53b1a28abde5c8b59b4/la-trasformazione-modalita-compatibilita.jpg)












