Matematica e logica. Mettiti alla prova - Pagine in anteprima · Test di logica 19 Le...

Test di logica 17

ESERCIZI SVOLTI15. Siano: p = “Il Sole è una stella”, q = “5 è un numero maggiore di 10”. Scegliere l’affermazione falsa tra le seguenti:A ~(p ∧ q)B (p ∨ q) ∧ p C (p ∧ q) ∨ ~p D (p ∧ q) ∨ p

SVOLGIMENTO Visto che p è vera e q è falsa, p ∧ q è falsa. Dunque la A è vera. Inoltre, p ∨ q è vera e nella B va in AND con una proposizione vera. Pertanto anche la B è vera. La C e la D esprimono un OR tra una proposizione falsa e una proposizione che nella C è falsa e nella D è vera. Ne consegue che la C è falsa mentre la D è vera. Concludiamo che l’unica affermazione falsa è la C.

16. Si consideri l’enunciato: “Ho incontrato Alice che stava correndo”. Poniamo p = “Ho incontrato Alice”, q = “stava correndo”. Scegliere la formula logica che esprime lo stesso enunciato.

A (p ∧ q)B (p ∨ q)C (p ∧ ~q)D Nessuna delle precedenti

SVOLGIMENTO L’enunciato è vero se p e q sono entrambe vere. Si tratta della congiunzione. La risposta corretta è la A.

17. Scegliere la negazione di: “Il cane abbaia e salta”.

A Il cane non abbaia e non saltaB Il cane non abbaia e saltaC Il cane abbaia o saltaD Il cane non abbaia o non salta

SVOLGIMENTO La risposta corretta è la D, come ci suggeriscono le formule di De Morgan.

18. Scegliere la negazione di: “Il cane abbaia o morde”.

A Il cane non abbaia e non mordeB Il cane non abbaia e mordeC Il cane abbaia e mordeD Il cane non abbaia o non morde

SVOLGIMENTO La risposta corretta è la A, come ci suggeriscono le formule di De Morgan.

Mate_Logi.indb 17Mate_Logi.indb 17 02/04/2013 15.47.3502/04/2013 15.47.35

18 Capitolo 1

1.3.2 Se, solo se, se e soltanto seL’implicazione logica lega due proposizioni, si indica con p ⇒ q e formalizza il nostro quotidiano modo di dire “Se… allora …”. La proposizione p viene detta ipotesi e q viene detta tesi. Per illustrare questa operazione consideriamo le due proposizioni p = “C’è neve”, q = “La strada è chiusa” e l’implicazione “C’è neve” ⇒ “La strada è chiusa” che usualmente esprimiamo come “Se c’è neve allora la strada è chiusa”. La nostra frase può essere formulata anche in uno qualunque dei modi seguenti:

• p è condizione sufficiente affinché si verifichi q, ossia “basta che ci sia neve per esser certi che la strada è chiusa”.

• q è condizione necessaria per la possibilità di p: “è necessario che la strada sia chiusa affinché si possa ritenere che c’è neve” o anche “solo se la strada è chiusa ci può essere neve” (naturalmente il fatto che la strada sia chiusa non è sufficiente ad assicurarci che ci sia neve, dal momento che può esserlo anche per altri motivi come frane, allagamenti, o per la domenica ecologica).

Che cosa succede invece se non c’è neve? L’enunciato non lo dice: la strada può essere sia aperta sia chiusa e in entrambi i casi non viene lesa la verità dell’impli-cazione. Essa è invece violata quando c’è neve e la strada è aperta. Potremmo del resto formulare la nostra frase anche come: “O la strada è chiusa o non c’è neve”. Riepilogando, in altre parole si può dire che:

• una condizione è sufficiente quando il suo verificarsi comporta il verificarsi della conseguenza (ma il suo non verificarsi non impedisce il verificarsi della conseguenza);

• una condizione è necessaria quando il suo non verificarsi comporta il non verificarsi della conseguenza (ma il suo verificarsi non garantisce il verificarsi della conseguenza); è ciò che secondo una formula latina viene detto condicio sine qua non.

Prende il nome di antinominale l’implicazione costruita come ~q ⇒ ~p che è del tutto equivalente a p ⇒ q. Nel caso dell’esempio di poc’anzi l’antinominale è “Se la strada è aperta allora non c’è neve”.

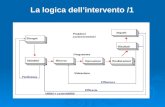
È molto efficace la seguente rappresentazione grafica, in cui si mette in evidenza come, nell’insieme dei casi possibili, la nostra implicazione indichi semplicemente che l’ipotesi “c’è neve” è un sottoinsieme dei casi in cui “la strada è chiusa”.


Test di logica 19

Le argomentazioni appena esposte dovrebbero portarci a condividere la tavola di verità che la logica ha deciso per l’implicazione: essa è sempre verificata a parte il caso in cui p è vera e q è falsa.

Implicazione logica

p q p ⇒ q

0 0 10 1 11 0 01 1 1

Se, nonostante il nostro preambolo, la tabella precedente continua a suscitare per-plessità non c’è da preoccuparsi. I logici stessi distinguono vari tipi di implicazione: questa, che fa parte della logica formale, viene detta anche implicazione materiale o filoniana, da Filone di Megara (IV secolo a.C.). Ma ci sono anche l’implicazione di Diodoro, che viene oggi ripresa nella logica temporale, e quella di Crisippo, che viene ripresa nella logica modale e prende il nome di implicazione stretta. Il fatto è che nell’implicazione materiale non viene necessariamente richiesto un qualche nesso tra le due proposizioni. Pertanto le due implicazioni.

• “Parigi è la capitale della Francia” ⇒ “10 è divisibile per 2”• “Parigi è la capitale d’Italia” ⇒ “10 è divisibile per 3”

risultano entrambe “vere”. E cosa ha a che fare Parigi con la divisibilità dei numeri? Assolutamente niente, ma ciò non importa. La cosa importante è che la tabella ci consenta deduzioni corrette quando la usiamo.

Per riassumere, l’implicazione logica p ⇒ q si esprime in vari modi. Si dice che:

• Se è vera l’ipotesi p allora è vera la tesi q.

• Se è falsa la tesi q allora è falsa l’ipotesi p.

• Solo se è vera la tesi q allora può essere vera l’ipotesi p.

• La verità dell’ipotesi p è condizione sufficiente affinché sia vera la tesi q.

• La verità della tesi q è condizione necessaria affinché possa essere vera l’i-potesi p.

• O p è falsa o q è vera.

Come esercizio, si provi a costruire le tavole di verità di:

⇒~ ~q p

∨~ p q

∧~ ( ~ )p q

e a controllarne l’equivalenza con p ⇒ q.


32 Capitolo 2

La seconda mostra invece test effettivamente proposti nelle prove d’ingresso, che si risolvono usando le conoscenze logico-matematiche elementari.

2.1.1 Esercizi “storici”Questo “ripasso”, costruito in gran parte su una scelta di esercizi classici (tra parentesi è a volte indicata la fonte) che si possono trovare in Internet, ci guiderà alla corretta risoluzione di vari test. Anche se, naturalmente, non esistono tecniche risolutive universali, riteniamo che i buoni esempi aiutino. Si presti attenzione a non dare una risposta “di getto”, perché in questi casi di solito è sbagliata.

ESERCIZI SVOLTI1. Per la strada che porta a Camogli passava un uomo con sette mogli. Ogni moglie aveva sette sacche, in ogni sacca aveva sette gatte, ogni gatta aveva sette gattini. Fra gatti, gatte, sacche e mogli in quanti andavano, dimmi, a Camogli?

SVOLGIMENTO Si tratta di una nota fi lastrocca che pone in fondo una semplice domanda. La risposta è legata solo alla nostra comprensione della moltiplicazione come operazione sintetica di addizioni uguali. Le donne sono 7, le sacche 7 ⋅ 7 = 49, le gatte nelle sacche 7 ⋅ 7 ⋅ 7 = 343, i gattini 7 ⋅ 7 ⋅ 7 ⋅ 7 = 2401. Dunque la som-ma fa 2800. Si potrebbe anche intendere che la fi lastrocca chieda di aggiungere l’uomo al conteggio, nel qual caso il totale sarebbe 2801. Attenzione però all’er-rore diffuso di considerare come risposta 2401, che sono invece solo i gattini. L’esercizio è sostanzialmente identico a uno proposto su un papiro egizio di 4000 anni fa: “Un topo generò 7 topi; ognuno di questi altri 7 topi; ognuno di questi altri 7; e ognuno di questi altri 7. Quanti topi in tutto?”.

2. Un uomo possiede 100 denari e ogni giorno spende un decimo di quel che ha. Con quanto rimane dopo 12 giorni? (Fibonacci)

SVOLGIMENTO Il primo giorno ha 100 denari, spende = ⋅11

10010

s denari e resta

con ⎛ ⎞= − ⋅⎜ ⎟⎝ ⎠

11

1 10010

r denari. Il secondo giorno spende ⎛ ⎞= − ⋅⎜ ⎟⎝ ⎠

21 1

1 10010 10

s

denari e resta con ⎛ ⎞= −⎜ ⎟⎝ ⎠

⋅2

21

1 10010

r denari. Al dodicesimo giorno avrà

( )⎛ ⎞− = =⎜ ⎟⎝

⋅⎠

⋅12

1211 100 0,9 100 28,2429536481

10 denari.

3. Una donna porta delle uova al mercato. A un primo compratore vende la metà delle uova, più mezzo uovo. A un secondo vende la metà delle uova rimaste, più mezzo uovo. A un terzo vende la metà delle uova rimaste, più mezzo uovo. Così ha venduto tutte le uova che possedeva. Quante uova possedeva?


70 Capitolo 2

10. Stabilire quale numero va inserito per completare la serie:

8, 22, 50, 106, 218, 442, …

A 980B 890C 884D 654E 780

11. All’inizio del 2007 ho comprato alcune azioni che a fi ne anno hanno guadagnato il 10% del valore ma alla fi ne del 2008 hanno perso il 10% del valore. Rispetto al valore iniziale, quello fi nale è:A diminuito dell’1%B lo stessoC aumentato dell’1%D diminuito del 10%E aumentato del 10%

12. In un supermercato il 60% di clienti acquista arance, il 35% acquista mele, il 25% non acquista né mele né arance. Quanti acquistano entrambi i tipi di frutta?A 15% B 30% C 5% D 20% E Non si può rispondere

13. Delle risposte date a un test, il 30% sono sbagliate e 14 sono le risposte esatte. Da quante domande era composto il test? A 20 B 30 C 100 D 21

14. Un usuraio convince Giovanni, il quale spera di saldare presto il debito, a scegliere lui, che presta con un interesse mensile dell’1%, anziché la banca, che presta con un interesse semestrale del 5%. Entro quanti mesi Giovanni deve saldare in modo da non rimetterci?A 4 mesiB 5 mesiC 2 mesiD 6 mesi


Capitolo 3

Test di calcolo combinatorio

Il calcolo combinatorio, nonostante richieda per la sua comprensione solo sem-plici conoscenze di matematica elementare, presenta spesso problemi di difficile risoluzione. Esplicitamente previsto tra gli elementi di matematica da conoscere per affrontare i test d’ammissione, è di per sé oggetto di un numero scarso di esercizi, ma molto spesso viene coinvolto indirettamente in quesiti che ne sot-tintendono implicitamente un’adeguata padronanza, come avviene per esempio nel calcolo delle probabilità. Sintetica e chiara è la definizione che troviamo sull’enciclopedia Treccani alla voce calcolo combinatorio: “Parte dell’aritmetica che ha come scopo principale quello di contare i raggruppamenti di varia specie che si possono formare con oggetti o simboli”. Rispetto agli oggetti a disposizione (i caratteri alfabetici, i simboli per la sche-dina del totocalcio, gli atleti che aspirano a salire sul podio dei vincitori ecc.), i raggruppamenti che interessano il calcolo combinatorio sono caratterizzati da:

• numero di elementi da cui li si preleva;

• numero di elementi da cui sono composti;

• possibili ripetizioni;

• importanza dell’ordinamento.

Vediamo qualche esempio. Se ci interessa il numero dei possibili pronostici del totocalcio dobbiamo trattare con sequenze dove i simboli si ripetono e dove l’ordine è importante. Diverso è il caso in cui vogliamo completare in cinquina il terno suggeritoci in sogno: qui i numeri non si ripetono e l’ordine non è impor-tante. Nel compilare anagrammi occorre invece usare tutti e soli, e nello stesso numero, i caratteri della parola proposta, e l’ordine è fondamentale. Il respiro della matematica combinatoria è più ampio di quanto lasciano intendere gli elementi di calcolo che qui presentiamo: si pensi al problema di stabilire quanti sono i percorsi a vuoto di un assegnato labirinto. Nel 1998 un miliardario americano acquista un manoscritto del X secolo d.C. (originariamente ritrovato in una dipendenza della chiesa del Santo Sepolcro di Costantinopoli) e ne affida l’analisi al museo di Baltimora. Ecco che, dopo 12 anni di restauro, i raggi ultravioletti ci hanno quasi inviato un “fax” dal III

Cap03_32441_73-98.indd 73Cap03_32441_73-98.indd 73 04/04/2013 17.45.3104/04/2013 17.45.31

74 Capitolo 3

secolo a.C. (per ripetere un espressivo commento della scoperta), restituendo alla luce sulla pergamena (Figura 3.1), tra le altre cose, alcune opere del più grande matematico dell’antichità, Archimede.

Figura 3.1

In particolare, per l’argomento trattato in questo capitolo, segnaliamo che nel palinsesto si trova anche il primo esempio storico di analisi combinatoria. Lo scienziato effettua il conteggio dei 17 152 possibili quadrati costruibili con i pezzi dello Stomachion, un antico gioco di costruzione analogo al più noto Tangram. Le Figure 3.2 e 3.3 mostrano un quadrato e un’ombra con cappello realizzati accostando i suoi pezzi.

Figura 3.2

Cap03_32441_73-98.indd 74Cap03_32441_73-98.indd 74 04/04/2013 17.46.0404/04/2013 17.46.04

Test di calcolo combinatorio 91

29. Quanti anagrammi possono essere formati con le lettere della parola ROMA?

SVOLGIMENTO Poiché le lettere sono tutte diverse, il numero di anagrammi è dato semplicemente dal fattoriale del numero di lettere diverse della parola Roma, quindi = ⋅ ⋅ ⋅ =4! 4 3 2 1 24.

30. Il signor Bianchi ha sei amici A, B, C, D, E, F. Decide di visitarli tutti nei prossimi 3 giorni, al ritmo di 2 al giorno. Quante possibilità ci sono? Se vuole visitare A il primo giorno, a quante si riducono?

SVOLGIMENTO Il primo giorno può visitare due qualunque tra i 6 amici e pertanto

si hanno ⎛ ⎞

= =⎜ ⎟⎝ ⎠

6, 2

615

2C possibilità.

Il secondo giorno, avendone già visitati 2, ne rimangono 4, quindi si hanno ⎛ ⎞

= =⎜ ⎟⎝ ⎠

4, 2

46

2C possibilità. Infine il terzo giorno si ha solamente una possibilità

corrispondente ai 2 amici non ancora visitati, =2, 2 1C . Pertanto si hanno in

tutto ⋅ ⋅ =6, 2 4, 2 2, 2 90C C C diverse possibilità di fare visita agli amici. Se invece A viene visitato il primo giorno, le possibilità per il primo giorno sono 5 (coppie formate da A e uno qualsiasi degli altri 5 amici). Le possibilità

totali risultano quindi ⎛ ⎞⋅ =⎜ ⎟⎝ ⎠

45 30

2.

Si può osservare che il vincolo della visita di A nel primo giorno riduce di un terzo le possibilità di visite totali (90/3 = 30). Infatti, in assenza di vincoli, A può ricevere visita in un giorno qualunque dei tre, mentre, imponendo che A venga visitato il primo giorno, le altrettante possibilità di visita al secondo e al terzo giorno vengono scartate.

31. Un allevatore deve marchiare i suoi capi di bestiame con una serie di 5 caratteri formata da 2 lettere non ripetute da scegliere fra A, B e C, seguite da 3 cifre non ripetute da scegliersi fra le dieci del sistema decimale. Se l’allevatore possiede 1000 capi, il tipo di codifica è sufficiente per contrassegnare ciascun animale con un simbolo diverso?

SVOLGIMENTO Calcoliamo il numero dei simboli diversi che può ottenere. Con le tre lettere si possono formare 6 coppie diverse e cioè: AB, AC, BC, CB, CA, BA. Esse non sono altro che le disposizioni con n =3 e k = 2, quindi = ⋅ =3,2 3 2 6D . Analogamente si possono ottenere configurazioni di 3 cifre non ripetute scelte nel sistema decimale in un numero dato da = ⋅ ⋅ =10,3 10 9 8 720D . Dunque il numero di simboli diversi è dato da ⋅ =3,2 10,3 4 320D D , quindi i simboli a disposizione sono sufficienti.

32. 6 persone hanno a disposizione 6 sedie; in quanti modi diversi le possono occupare? Se le sedie a disposizione sono 4, in quanti modi diversi le possono occupare?

Cap03_32441_73-98.indd 91Cap03_32441_73-98.indd 91 04/04/2013 17.46.0904/04/2013 17.46.09

Test di calcolo combinatorio 97

12. Una società composta da 21 membri deve scegliere presidente e segretario. Quante sono le scelte possibili?A 42B 210C 420D 441E 41

13. Il ladro Arsenio sa che per aprire la cassaforte del miliardario Paperone deve comporre una “parola” di 3 lettere scelte fra le 21 lettere dell’alfabeto. Fiducioso della sua abilità, porta con sé la lista di tutte e parole possibili. Quanto è lunga la lista? A 9261B 4 084 101C 143 640D 64 827E 46

14. In quanti modi si possono mettere 7 palline distinte in 3 urne numerate, in modo che 3 palline siano nell’urna 1, 2 nell’urna 2 e 2 nell’urna 3?A 35B 2178C 343D 5040E 210

15. Una fabbrica produce cioccolatini di 4 tipi e confeziona scatole da 7 cioccolatini ciascuna. Quanti sono i possibili assortimenti?A 210B 120C 2401D 16 384E 35

16. Una commessa sistema 10 scatole identiche di cioccolatini su 5 scaffali. In quanti modi diversi può farlo?A 2002B 252C 1002D 120E 1001

Cap03_32441_73-98.indd 97Cap03_32441_73-98.indd 97 04/04/2013 17.46.1104/04/2013 17.46.11

Capitolo 4

Test di calcolo delle probabilità

Il calcolo delle probabilità si interessa di quei fenomeni del mondo reale ai cui possibili esiti si associa una situazione di incertezza, come il tempo che farà do-mani, l’uscita di un numero nel lancio di un dado o nell’estrazione alla tombola, la rendita entro il mese prossimo del titolo che ho acquistato ieri sul mercato finanziario ecc. Possiamo vedere l’incertezza come dipendente dalla mancanza di conoscenza su: le variabili in gioco che determinano l’evento, l’errore che commettiamo nel misurarle, l’individuazione delle leggi che lo regolano o altro ancora. Il calcolo delle probabilità vuole offrire una misura scientifica di questa incer-tezza. Le sue origini sono legate all’antico gioco dei dadi, e i suoi primi concetti si trovano nel De ludo aleae Liber (Figura 4.1) di Girolamo Cardano (1501-1576) e in Sopra la scoperta de i dadi di Galileo Galilei (1564-1642); in particolare, in quest’ultimo scritto, sembra su richiesta del Gran Duca di Toscana, si vuole deter-minare la probabilità delle possibili somme dei risultati del lancio di tre dadi.

Figura 4.1


100 Capitolo 4

Forse il problema era già stato risolto da Cardano e Galilei può esserne venuto a conoscenza, ma egli esprime con spirito didattico e chiara visione dei vari aspetti coinvolti il motivo per cui il 10 è più probabile del 9 anche se i due esiti si ottengono da un uguale numero di figure dei tre dadi. Nonostante questi antefatti, la nascita del calcolo delle probabilità viene solitamente legata agli studi di Blaise Pascal, cui si era rivolto nel 1654 il Cava-liere De Meré, giocatore di professione, con specifiche domande: Si ottiene più facilmente un 6 lanciando 4 volte un dado o un 12 lanciando 24 volte una coppia di dadi? Come mai il gioco effettivo tradiva la proporzione “6 (possibilità di un dado) sta a 4 come 36 (possibilità di due dadi) sta a 24”? Pascal rimase affa-scinato dalle questioni cogliendone l’aspetto scientifico e coinvolse nello studio Pierre Fermat. Tuttavia, solo all’inizio dell’Ottocento la probabilità ebbe la sua definizione classica a opera di Laplace e, soprattutto, venne applicata anche a temi diversi da quello del gioco, quali l’astronomia, la biologia, l’epidemiologia, il calcolo dei premi assicurativi ecc., e si aprì a tutti i campi della sperimentazione scientifica. Anche la logica estende il suo impianto classico bivalente imperniato sui due unici valori ammessi (tertium non datur!) e studia gli enunciati associando a ciascuno un numero che misura la sua probabilità di essere vicino al vero.

4.1 Spazio campionarioMentre per i capitoli precedenti abbiamo potuto presupporre una cultura uniforme sull’argomento da parte dei nostri lettori, qui la situazione è più variegata e ci sembra importante iniziare richiamando più in dettaglio la terminologia in uso. Si dice aleatorio un esperimento cui si associa un ben definito insieme di risultati, tutti possibili ma a priori nessuno certo. Come classico esempio ricordiamo il lancio di un dado regolare a 6 facce. Si dice spazio campionario o spazio campione associato a un esperimento l’insieme S di tutti i possibili esiti. Qui supporremo, essendo questa una condizione cui si limitano i test, che S sia sempre un insieme finito.

Esempia. Si lancia un dado a 6 facce. I possibili risultati (esiti) sono i 6 numeri scritti

sulle facce. Dunque lo spazio campione è l’insieme { }= 1, 2, 3, 4, 5, 6 .Sb. Si lancia una moneta due volte di seguito. I possibili risultati a ogni lancio

sono T (testa) o C (croce). Trattandosi di due lanci, lo spazio campione è l’insieme di 4 elementi { }= TT, CC, TC, CTS .

Si dice evento un sottoinsieme di S, cioè un insieme di risultati possibili, e si dice evento elementare ogni elemento dello spazio campione S. Se A è un evento di S, e ∈ s S è il risultato di un esperimento, si dice che si è verificato A quando ∈s A e si dice che non si è verificato A nel caso contrario, cioè quando ∉ .s A L’evento costituito da tutto lo spazio S è sempre verificato e si dice evento certo, mentre l’evento vuoto ∅ non si verifica mai e si dice evento impossibile.


Matematica e logica. Mettiti alla prova - Pagine in anteprima · Test di logica 19 Le...

Documents

Transcript of Matematica e logica. Mettiti alla prova - Pagine in anteprima · Test di logica 19 Le...