La manipolazione nell'apprendimento del concetto di numero fra scuola

dell'infanzia e scuola primariaMariolina Bartolini Bussi

Univesità di Modena e Reggio Emiliabartolini@unimore.it

con contributi di Mara Boni, Rita Canalini e Franca Ferri

Modena, 6 settembre 2011

Le rappresentazioni di quantità sono (forse) le più antiche tracce scritte nella storia dell’uomo.

Un tema universale

Osso di babbuino (Africa)35.000 anni fa

In tutti i paesi del mondo i numeri e l’aritmetica sono parte della prima alfabetizzazione dei bambini, anche nelle scuole poverissime

Un tema universale

Neuroscienze

La ricerca ha messo in evidenza la presenzacontemporanea di:Un sistema per rappresentare in modo

approssimato grandezze numeriche anche grandi;Un sistema per rappresentare in modo preciso

piccoli numeri di singoli oggetti.Questi sistemi prendono in conto le nostre intuizioni

numeriche fondamentali e servono come fondamento per I concetti numerici più sofisticatiche sono unicamente umani.

Feigenson, L.; Dehaene, S. & Spelke, E. (2004)

Neuroscienze

La ricerca ha messo in evidenza la presenzacontemporanea di:Un sistema per rappresentare in modo

approssimato grandezze numeriche anche grandi;Un sistema per rappresentare in modo preciso

piccoli numeri di singoli oggetti.Questi sistemi prendono in conto le nostre intuizioni

numeriche fondamentali e servono come fondamento per I concetti numerici più sofisticatiche sono unicamente umani.

Feigenson, L.; Dehaene, S. & Spelke, E. (2004)

misura

numerosità

Come si apprendono i numeri?

• Principio di Iniettività (Gelman & Gallistel)

Primo principio descritto nel modello che governa e definisce il processo del contare a parole secondo Gelman & Gallistel. Il bambino assegna una, e solo una, parola per contare a ciascuno degli oggetti che devono essere contati. In questo modo si realizza una corrispondenza biunivoca tra l’insieme delle parole per contare utilizzate e l’insieme degli oggetti da contare. Il principio di iniettività non è rispettato se si conta due volte lo stesso oggetto, se si usa due volte la stessa parola, se si salta qualche oggetto. Non è richiesto che le parole utilizzate siano numerali e neppure che, nel caso che lo siano, vengano utilizzati secondo la sequenza usuale (uno, due, tre, quattro, ecc.).

Modello di Gelman & Gallistel

Principio di ordine stabile (Gelman & Gallistel)

• Secondo principio descritto nel modello che governa e definisce il processo del contare a parole secondo Gelman & Gallistel. Il bambino utilizza le parole per contare secondo una sequenza stabile, cioè ripetibile. Non è richiesto che la sequenza sia quella usuale: può accadere che la sequenza usata stabilmente sia, ad esempio, uno, due, quattro, sei.

Principio di cardinalità (Gelman & Gallistel)

• Terzo principio descritto nel modello che governa e definisce il processo del contare a parole secondo Gelman & Gallistel. Il bambino riconosce nell’ultima parola pronunciata una proprietà (numerosità, cardinalità) dell’intero insieme.

Modello di Gelman & Gallistel

Principio di astrazione (Gelman & Gallistel)

• Quarto principio descritto nel modello che governa e definisce il processo del contare a parole secondo Gelman & Gallistel. Il bambino ammettaela possibilità ed è in grado di contare oggetti di qualsiasi natura, sia presenti, sia evocati o solo pensati.

Principio dell’irrilevanza dell’ordine (Gelman & Gallistel)

• Quinto principio descritto nel modello che governa e definisce il processo del contare a parole secondo Gelman & Gallistel. Il bambino riconosce che il conteggio non dipende dall’ordine in cui sono contati gli oggetti, cioè che è inessenziale quale parola numero è assegnata ad un certo oggetto.

Modello di Gelman & Gallistel

Come si apprendono i numeri?

Modello di ridescrizione rappresentazionale di Annette Karmiloff Smith

applicato al caso dei numeri.

“un modo tipicamente umano di raggiungere la conoscenza consiste nel fatto che la mente possasfruttare internamente l’informazione giàimmagazzinata (sia essa innata o acquisita) ridescrivendo le sue rappresentazioni o, piùprecisamente, rappresentando in modo nuovo ciòche le rappresentazioni interne già codificano”.

Come si apprendono i numeri?

Modello di ridescrizione rappresentazionale di Annette Karmiloff Smith

applicato al caso dei numeri.

EsperienzePratiche ripetuteManipolazioneConsolidamento

Molto dipende da una dinamica interna.

MACome favorire la ridescrizione?

Artefatto: è una parte dell’ambiente materiale deliberatamente modificata dall’uomo per essere utilizzata con un’intenzione precisa.

Esempi:Le mani per contareIl pallottoliereLe bacchette - cannucceL’abacoIl righello (o linea dei numeri)La pascalinaBee-botAmbienti virtuali (micromondi): es. Focus on bee-bot

Numeri e artefatti

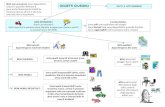
Problemi additivi

(addizione e sottrazione)

Bee-botCardinalità, ordine, comando,

MisuraOrientamento spaziale ……

Costruzione numeri

CardinalitàRaggruppa

mento (dieci)

Linea dei numeriOrdine

Lettura / scrittura

Precedente – successivo

PascalinaLettura

/scrittura+1-1

u, da ….Add. Sottr.

Abacou, da ….

Add. Sottr.

Campi di esperienza

(micromondi)

didattici

Un progetto appena avviato2011-2014

Scuole delle province di Torino, Bologna e Reggio Emilia

Difficoltà di apprendimento in matematica

M. Bartolini Bussi – Anna Baccaglini FrankGiacomo Stella – Maristella Scorza

Un progetto in corso di pubblicazione (DVD)

Le mani che toccano, afferrano, manipolano, accarezzano, indicano, sono cognitivamente molto diverse dalle mani che contano. Nel secondo caso c’è, infatti, l’intenzionalità di utilizzarle per uno scopo che non era quello originario e naturale. I primati non umani usano le mani e le dita anche in modi estremamente raffinati, ad esempio per estrarre il cibo da un contenitore o battere una pietra per rompere noci di cocco. Non c’è invece nessuna osservazione che documenti, nei primati non umani, l’uso delle mani e delle dita per contare (ad eccezione, forse, del caso di quelli addestrati al linguaggio dei segni). Dunque l’utilizzo delle mani per contare richiede il distanziamento dalla mano come parte del proprio corpo e il controllo cosciente dell’azione che si compie. La mano diviene quindi un artefatto, una parte del mondo materiale deliberatamente trasformata per compiere un’azione diversa da quelle naturali.

Le mani

Le mani

Luca Pacioli, 1494Beda, VII secolo

Brian Butterworth (1999), Intelligenza matematica, Milano: Rizzoli.

Capitolo 5Mani, spazio e cervello.

Le Dita, per disposizione della natura e per l’irrevocabile decisione del grande Aritmetico, sono state incaricate di

servire al conteggio, alla stregua di rapide e naturali cifre,

sempre pronte e sotto Mano ad assisterci nei nostri calcoli.(J. Buwler, Chirologia, 1644)

Le mani

B. Butterworth:La rete corticale attivata quando si stanno elaborando numeri è parzialmente sovrapposta con quella utilizzata per il movimentodelle mani e delle dita.

L’agnosia digitale(incapacità di rappresentare mentalmentele proprie dita)è un predittore delle difficoltà aritmetiche.Nella sindrome di Gerstmannsono presenti agnosia digitale e discalculia.

Le mani e il cervello

Già nella scuola dell’infanzia …quanti anni hai?

inf

Già nella scuola dell’infanzia …

inf

Già nella scuola dell’infanzia …quanti anni hai?

inf

Qualche idea in prima elementare

(insegnante Rita Canalini)

“ Disegna le tue mani

mentre contano”.

Contare sulle dita nella scuola elementare

RC

Contare sulle dita nella scuola elementare

RC

Dieci come le nostre dita!

RC

RC

Ricerca – azione nelle scuole comunali di Modena (oltre 20 insegnanti).

Scuola dell’infanzia: pallottoliere

inf

Schema del percorso

Che cos’è?

Come è fatto?

Che cosa fa?

Perché lo fa?

inf

Che cos’è?Apertura della conversazione quando l’insegnante mostra ai bambini il pallottoliere già montato.E’ la voce del narratore.Lo scopo è multiplo. L’insegnante vuole far:Evocare la memoria di esperienze;Collegare con altre esperienze;problematizzare (il bambino deve sentire il problema come suo)Imparare il nome “convenzionale” (pallottoliere, che comincia come PALLina).Possibili variazioni Avete mai visto una cosa così?Ne abbiamo a scuola? Sono uguali?Come si chiama?

Che cos’è?

Come è fatto?

Che cosa fa?

Perché lo fa?

inf

Come è fatto?Questo lancio (o rilancio) rappresenta l’entrata in gioco della voce del costruttore.Lo scopo è multiplo. L’insegnante vuole far:rappresentare (verbalmente) le parti dell’artefatto;identificare le componenti e denominarle in modo corretto (aste, fili, palline forate, ecc.)descrivere le relazioni spaziali delle parti con l’uso di opportuni locativi (sopra, sotto, a fianco, dentro, ecc.)descrivere le funzioni delle varie parti (stare in piedi, scorrere, ecc.)Possibili variazioni:Che cosa ci serve per costruirne un altro?Come possiamo dare le istruzioni per costruirne uno così?

Che cos’è?

Come è fatto?

Che cosa fa?

Perché lo fa?

inf

Artefatto: oggetto materiale o simbolico in sé. Strumento: entità mista composta sia da componenti

legate alle caratteristiche dell’artefatto che da componenti soggettive (schemi d’uso messi in campo da un soggetto quando è assegnato un compito da risolvere con l’aiuto di un artefatto). Gli schemi d’uso dipendono dall’artefatto, variano a seconda del compito e, per lo stesso compito, variano da individuo a individuo.

Rif. Rabardel, P. (1995). Les hommes et les technologies, approche cognitive des instruments contemporains. Armand Colin : Paris.

Artefatti e schemi d’uso

Che cosa fa?Si passa ad aspetti funzionali. In alcuni casi le insegnanti predispongono attività specifiche(es. gioco dei birilli) o riprendono attività tradizionali (es. appello) proponendo l’artefatto come aiuto per lo svolgimento del compito. Questo lancio (o rilancio) rappresenta l’entrata in gioco della voce dell’utilizzatore.Lo scopo è multiplo. L’insegnante vuole far:praticare la filastrocca dei numeri(contare le palline) e praticare l’uso del pallottoliere nelle ordinariesituazioni di conteggioPossibili variazioniChe cosa possiamo fare con il pallottoliere?A che cosa serve? Come funziona?Possiamo usarlo quando facciamo l’appello?Durante l’appello: proviamo ad usarlo.

Che cos’è?

Come è fatto?

Che cosa fa?

Perché lo fa?

inf

Perché lo fa?E’ la giustificazione dell’efficacia del suo utilizzo. Questo lancio (o rilancio) rappresenta l’entrata in gioco della vocedel “teorico”. In questo l’insegnante assume in pieno il ruolo del mediatore culturale.L’insegnante vuole far:ricostruire in modo consapevole il sapere matematico accumulato (sedimentato, depositato)sull’artefatto.Possibili variazioni:Spiega bene come si usa per essere sicuri di non sbagliare.(mostrando un pupazzo che sbaglia ad usarlo) Fa bene o fa male? Perché?

Che cos’è?

Come è fatto?

Che cosa fa?

Perché lo fa?

inf

Schema del percorso

Che cos’è?

Come è fatto?

Che cosa fa?

Perché lo fa?

Domande “tipiche” di una didattica laboratoriale.

inf

• Non solo azione …..

ma anche rappresentazione con diversi sistemi semiotici

(il disegno, la messa in forma di un modello … ecc.)

Un tratto comune

Il pallottoliere può essere (ri)esplorato come avvio alla notazione posizionale in base dieci.

E nella scuola elementare?

RC

Perché ad ognuno un “personale” artefatto/strumento?Tre i motivi principali:

1. l’artefatto strumento acquista un peculiare valore affettivo

RC

2) una dotazione individuale di strumenti consente di ricorrervi frequentemente consentendo la reiterazione di gesti e schemi d’uso chiamati, progressivamente, con tempi distesi e grazie all’interazione sociale, ad essere interiorizzati

3) l’assemblaggio-realizzazione dell’artefatto viene proposta dall’insegnante secondo modalità che tendono a far emergere, almeno in parte, il sapere incorporato nello strumento e/o a far ipotizzare schemi d’uso

RC

Un esempio, l’assemblaggio del pallottoliere:

• Per ogni bambino si preparano dei sacchetti contenenti due stanghette in legno, due rettangoli in legno o cartone, ciascuno con 2 fori e 20 perline (pasta forata)

• L’insegnante mostra il contenuto di uno dei sacchetti, le palline vengono contate, e dichiara che sono i pezzi necessari per costruire uno strumento che si chiama pallottolliere e che serve per contare e calcolare. Dichiara di aver perso le istruzioni di montaggio quindi occorre ipotizzare come lo strumento debba essere montato

• Ad ogni allievo viene consegnato il materiale e ciascuno lo esplora provando a realizzare il pallottoliere

• Dopo qualche tempo, si discute sulle varie realizzazioni proposte

RC

Dalla discussione emerge che • in ogni stanghetta vanno infilate 10 palline tante

quante sono le dita delle nostre mani (riferimento all’idea di raggruppamento)

• i rettangoli di legno servono per infilare le due stanghette, dunque non far uscire le palline (ogni strumento è anche il prodotto di soluzioni tecnologiche e come tale ha potenzialità e vincoli)

• la lunghezze delle stanghette è solo in parte occupata dalle palline così, mentre si conta, si possono separare quelle contate da quelle che si devono ancora contare (riferimento al processo di ripartizione , cfr. Gelmann e Gallistel)

RC

La cifra a sinistra “conta” la “fila-decina”

RC

La cifra a sinistra “conta” la “fila-decina”

La cifra a sinistra conta la fila-decina che abbiamo circondato con una linea chiusa.La cifra a destra conta le unità.

RC

Pallottoliere e “calcolo mentale”

RC

Pallottoliere e “calcolo mentale”

Vedo due file-decina sul pallottoliere

RC

Pallottoliere e “calcolo mentale”

Vedo due file-decina sul pallottoliere

Sposto una fila-decina

RC

Pallottoliere e “calcolo mentale”

Vedo due file-decina sul pallottoliere

Sposto una fila-decina

Sposto 7 palline senza contarle perché ne lascio 3 a sinistra(subitizing)

RC

Pallottoliere e “calcolo mentale”

Vedo due file-decina sul pallottoliere

Sposto una fila-decina

Sposto 7 palline senza contarle perché ne lascio 3 a sinistra(subitizing)

20 = 10 + 10

20 – 10 = 10

7 + 3 = 10

20 – 17 = 20 – 10 – 7 = 3

RC

Pallottoliere e “calcolo mentale”

COMPITO

AZIONI sull’ARTEFATTO

SCHEMI D’USO

RC

Pallottoliere e “calcolo mentale”

COMPITO

AZIONI sull’ARTEFATTO

SCHEMI D’USO

SIGNIFICATI MATEMATICI

20 = 10 + 10

20 – 10 = 10

7 + 3 = 10

20 – 17 = 20 – 10 – 7 = 3

RC

Mediazione semiotica

Il sostantivo mediazione deriva dal verbo mediare

e si riferisce a un processo con una complessa struttura che

include i partecipanti e le circostanze che sono potenzialmente

rilevanti in questo processo:

- qualcuno che media, il mediatore;

- qualcosa che viene mediato, il contenuto rilasciato dalla

mediazione;

- qualcuno soggetto alla mediazione, il ricevente a cui la

mediazione apporta differenze;

- la circostanza della mediazione;

- i mezzi della mediazione, la modalità;

- il luogo, il sito in cui la mediazione può avvenire. (Hasan)

Compito

Attività Semiotica

Allievo(i)

culturaSapere

Matematico Produzioni collettive

“Testi” matematici

Produzioni individuali

“Testi ”situati

Ruolo dell’insegnante

Bacchette (cannucce) e fascetti

Bacchette, fascetti, unità, decine

55

1 elementare / 1 semestre

Prima conta dieci bastoncini, lega un

fascetto. Quando hai fatto come conti?

1 da dieci e 1 da uno fa dieci uno

(+ —)

Dalla nostra tradizione

Conti Alberto, Aritmetica per la prima classe elementare , Firenze, Bemporad e Figlio, 1920,

Nota per l’insegnante. Il centesimo, il soldo [5 cent.] e il soldone *10 cent.+ sono d’uso così familiare che molti insegnanti ritengono opportuno di valersene fin dalla prima classe per la rappresentazione concreta dei primi 20 numeri. Però per classi numerose appare poco pratico l’uso di queste monete, in luogo delle quali si preferisce fare uso dei dischi di carta.Certamente l’uso del soldo e del soldone implica un concetto di sostituzione e di equivalenza, che in un primo grado d’istruzione offre difficoltà che non conviene aggiungere alle altre difficoltà offerte dai primi passi. Noi riteniamo preferibile che il fanciullo abbia sotto gli occhi tanti oggetti quante sono le unità del numero rappresentato e troviamo assai pratico l’uso degli stecchini sciolti, e a mazzetti, e a fasci.

Dalla nostra tradizione

36 - 28

Cina – Prima Elementare

Da un libro cinese

Cina – Prima Elementare

36 - 28

Da un libro cinese

problema

36 – 28?

Valore posizionale

36 -28=12?

?

problema

?

36 – 28?

Valore posizionale

problema

Slego un fascetto e prendo i

bastonciniche mi servono

?

36 – 28?

Valore posizionale

problema

Valore posizionale

?

36 -28=

8..

con il “prestito” di una decina

36 – 28?Slego un fascetto e prendo i

bastonciniche mi servono

problema

Legareslegare

36 -28=

8..

con il “prestito” di una decina

Valore posizionale

36 – 28?

problema

Legareslegare

36 -28=

8..

con il “prestito” di una decina

Valore posizionale

36 – 28?

ComporreScomporre

Linea dei numeri

Linea dei numeri

RC

Realizzazione della linea dei numeri• Attività di realizzazione di una

linea come la seguente: (la “finestra” può essere spostata avanti e indietro e “nasconde” il numero precedente e il successivo). I numeri maggiori si “incontrano” spostando la finestra da sinistra verso destra, viceversa per i minori

• A terra viene realizzata una linea fino a 15…: i numeri maggiori si incontrano “camminando in avanti” i numeri minori “camminando all’indietro”

• compiti che implicano il ricorso all’artefatto-strumento

RC

Compito

Attività Semiotica

Allievo(i)

culturaSapere

Matematico Produzioni collettive

“Testi” matematici

Produzioni individuali

“Testi ”situati

Ruolo dell’insegnante

Pascalina

Zero+1 – Quercettida un’idea di F. Arzarello

Pascalina

Nota storica: la pascalina

…. invenzione che consente di eseguire ogni genere di operazione aritmetica, in modo nuovo e comodo …..Questa macchina semplifica ed elimina nelle sue operazioni tutto quanto è superfluo, il più incompetente troverà tanti vantaggi quanto il più esperto. Senza trattenere o prendere a prestito nulla, la macchina fa da sola quanto l’operatore desidera, senza che lui se ne debba in alcun modo preoccupare.

(B. Pascal, 1645)

Nota storica: la pascalina

William Schickard

1623

Nota storica: la pascalina

Klein (1924) così commenta il senso delle macchine da calcolo ed in particolare della Brunsviga.

Nota storica: la pascalina

Mi sia permesso riassumere osservando che il principio teorico della macchina è molto elementare e rappresenta semplicemente una realizzazione tecnica delle regole che si usano sempre nel calcolo numerico […].

(Felix Klein)

Nota storica: la pascalina

Nell’esistenza di una tale macchina vediamo una incontestabile conferma che solo le regole dell’operazione, e non il significato dei numeri, sono importanti nel calcolo; perché la macchina può seguire solo queste; è costruita per fare esattamente questo; non potrebbe cogliere intuitivamente il significato dei numeri.

(Felix Klein)

Nota storica: la pascalina

Non riterremo dunque accidentale che un uomo come Leibniz, pensatore astratto di primo livello, e uomo di grande talento pratico, sia stato, al tempo stesso, sia il padre della pura matematica formale che l’inventore di una macchina calcolatrice.

(Felix Klein)

Alcuni significati matematici:

Rappresentazione polinomiale dei numeri in base dieci.

Algoritmi di addizione e sottrazione in base dieci.

Collegamento tra aspetti semantici ed aspetti sintattici.

(classi prima e seconda elementare)

(Mara Boni)

Rappresentazionepolinomiale dei numeri.

Collegamento tra aspetti semantici e

sintattici

Conta usando la pascalina

Prima elementare: Mara BoniMB

Conta usando la pascalina

Prima elementare: Mara Boni

Rappresentazionepolinomiale dei numeri.

Collegamento tra aspetti semantici e

sintattici

MB

Dentro lo schema

La risposta di Alice, colta al volo dall’insegnante e proposta a tutti come modello da imitare, mette a disposizione di tutti il collegamento tra

Artefatto (le ruote, andare avanti, girare, i gesti, diventa, l’uno che si mette con un altro uno, diventa …)

Matematica (i numerali nell’ordine standard, l’operatore +1, …..).

MB

Dentro lo schema

La risposta di Alice, colta al volo dall’insegnante e proposta come modello da imitare, mette a disposizione di tutti il collegamento tra

Aspetti sintattici (la conta realizzata in modo automatico)

Aspetti semantici (il numero degli scatti necessari)

MB

Qualche mese dopo(seconda elementare)

Prova individuale con una pascalina a testa:

Costruisci il numero 23 e spiega con parole e disegni come hai fatto (partendo da zero).

MB

Qualche mese dopo(seconda elementare)

MB

Qualche mese dopo(seconda elementare)

MB

Qualche mese dopo(seconda elementare)

MB

Sono schemi d’uso diversi …

Che sottendono significati matematici diversi:

23 = 0 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

23 = 2d + 3 u = 20 + 3

Secondo esempio(classe quarta elementare)

(Franca Ferri)

89

La consegna (individuale)

Scrivi le istruzioni d’uso della

Pascalina per l’operazione di

addizione

(caso particolare suggerito:

28 + 14)

FF

Due protocolli

Christian:

Ho scritto il primo addendo, 28, poi ho aggiunto il secondo, ruotando in senso orario la rotella delle unità quattro volte e la rotella delle decine una sola volta. Il risultato è 42.

Orlando:

Ho scritto il numero 28, poi ho girato in senso orario 14 volte la ruota in basso a destra, quella delle unità. Il risultato è 42.FF

Una nuova consegna

Guarda che cosa hanno scritto Christian e Orlando per calcolare sulla pascalina:

28 + 14

Prova a scrivere le espressioni matematiche che rappresentano i due diversi procedimenti.

FF

Una nuova consegna

Guarda che cosa hanno scritto Christian e Orlando per calcolare sulla pascalina:

28 + 14

Prova a scrivere le espressioni matematiche che rappresentano i due diversi procedimenti.

FF

Globalmente

• Usano solo i segni matematici (7/23)

• Usano segni matematici e linguaggio iconico (2/23)

• Usano segni matematici e linguaggio verbale (10/23)

• Usano segni matematici, linguaggio verbale e linguaggio iconico (4/23)

FF

Solo segni matematici (M. Y. N.)

Christian

= (20 + 10) + (4 + 8) =

= 30 + 12 =

= 42

Orlando

= (20 + 8) + (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1) =

= 20 + (8 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1) =

= 20 + 22 =

= 42

FF

Segni matematici e linguaggio iconico

FF

Segni matematici e linguaggio verbale

Le due operazioni sono le stesse, solo che cambia come le svolgono.

Christian: 28 + 1 da + 4 u = 42

Orlando: 28 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 42

(L. F.)

FF

Segni matematici, linguaggio verbale ed iconico (L. A.)

FF

Abaco

• assemblaggio del nuovo strumento secondo modalità analoghe a quelle descritte per il pallottoliere

• emerge un conflitto: perché una base e due stanghette verticali?

• Attraverso la “discussione matematica” si confrontano varie ipotesi finché dall’opacità dello strumento si passa alla trasparenza: la stanghetta a destra “conta” le unità da 0 a 9, quella a sinistra “conta” le decine (l’abaco “incarna” la notazione posizionale).

RC

L’abaco e la sua rappresentazione grafica

RC

L’abaco e il calcolo

RC

Una rete di artefatti/strumenti

RC

Una rete di artefatti, funzioni ipotizzate:

• Promuove un distacco dagli strumenti concreti, orienta la riflessione sui saperi matematici

• Rende più ricca e articolata l’attività di carattere semiotico relativa all’interazione con gli artefatti fisici, alla rappresentazione di tale attività e alla progressiva evoluzione di significati matematici

• Il dialogo fra strumenti può generare conflitti cognitivi produttivi rispetto alla costruzione di significati matematici

RC

Un giocattolo programmabile: bee-bot

Significati che possono essere mediati inizialmente.

- Numero (contare)

- Numero (misura)

- Spazio (sistema di riferimento)

- Spazio (percorso)

- Informatica (sequenza di istruzioni, memoria, ecc.)

Un giocattolo programmabile

Schema del percorso

Che cos’è?

Come è fatto?

Che cosa fa?

Perché lo fa?

Ad esempio

Descrivere accuratamente che cosa può fare bee-bot attraverso una esplorazione diretta.

• Movimenti semplici

• Movimenti complessi (percorsi su traiettorie aperte, percorsi su traiettorie chiuse)

• Forma delle traiettorie – esplorazione – scoperta di regolarità.

• E’ possibile far percorrere traiettorie poligonali?

• Di che tipo?

Esperimenti nella scuola dell’infanzia

inf

GIACOMO: IL PASSO DEL BEEBOT NON SORPASSA IL FOGLIO

MARCO: PERO’ SE FA DUE PASSI SORPASSA IL FOGLIO

GIACOMO: 3 PASSI SECONDO ME SONO TROPPI NE BASTANO 2inf

inf

inf

SAMIRA: POTREMMO METTERE DEI FOGLI COSI’ CAPISCI

ALESSIA G.: LI METTIAMO IN FILA

inf

PERCORSI CREATI DAI BAMBINI

inf

Bee-bot: il listato come oggetto

Disegnare la traiettoria del bee-bot su un foglio a quadretti.

Scrivere un programma che riporta a casa bee-bot sulla stessa traiettoria

Camminando all’indietro

Facendo mezzo giro e poi camminando in avanti

Bee-bot nella scuola elementare

AR

Schema generale

Produzione

individuale

di segni

Produzione

collettiva

di segni

Discussione

Matematica

Attività con

l’artefatto

(individuale – piccolo gruppo)

Problemi additivi

(addizione e sottrazione)

Bee-botCardinalità, ordine, comando,

MisuraOrientamento spaziale ……

Costruzione numeri

CardinalitàRaggruppa

mento (dieci)

Linea dei numeriOrdine

Lettura / scrittura

Precedente – successivo

PascalinaLettura

/scrittura+1-1

u, da ….Add. Sottr.

Abacou, da ….

Add. Sottr.

Campi di esperienza

(micromondi)

didattici

ringraziamentiMara Boni

Rita Canalini

Franca Ferri

Alessandro Ramploud

Maria Teresa Corradini

Susanna Stanzani

Maria Vittoria Vecchi

Insegnanti delle scuole comunali dell’infanzia (Modena)

Studenti, tirocinanti, laureandi e laureati del corso in Scienze della formazione Primaria (UNIMORE)