Capitolo 5: Filtri di uso comune nell’elaborazione dei ... 5.pdf · di filtro ricorsivo. Se si...

Corso di Laurea in Ingegneria Biomedica Elaborazione di Dati e Segnali Biomedici Filtri di uso comune nell’elaborazione dei segnali biomedici

Capitolo 5:

Filtri di uso comune nell’elaborazione dei segnali biomedici

5.1 Filtri Numerici: Definizioni e Richiami Un filtro numerico ha la stessa funzione di un filtro analogico solo che ne differisce

sostanzialmente nella realizzazione. I filtri analogici sono realizzati utilizzando circuiti elettronici attivi o passivi e operano su segnali continui. I filtri numerici sono realizzati usando sia circuiti logici che algoritmi software ed operano su sequenze di numeri ottenute campionando i segnali continui.

I filtri numeri offrono una serie di vantaggi rispetto a quelli analogici. Essi sono immuni da rumore per il modo in cui sono realizzati. La loro accuratezza dipende solo dal numero di bits con cui si è scelto di rappresentare le variabili numeriche. Le caratteristiche operative possono essere facilmente e con poco onere cambiate, ed al contrario dei filtri analogici le loro prestazioni non dipendono da fattori quali l’età dei componenti, variazioni della temperatura e dalla tensione di rete.

In genere un filtro numerico è rappresentato da un sistema a tempo discreto, lineare, tempo invariante, causale al cui ingresso è posta una sequenza di numeri che indicheremo con xn e in uscita una sequenza numerica yn. Tale sistema può essere rappresentato dalle equazioni alle differenze:

∑∑−

=−

−

=− •=•

1'

1'

N

oiini

N

oiini xayb

dove N rappresenta l’ordine del sistema e risulta b’

N ≠ 0. L’equazione precedente può essere riscritta nella:

∑∑−

=−

−

=− •−•=

1

1

'1

'N

iini

N

oiinin ybxay

A volte, in questa equazione, le due sommatorie hanno due ordini diversi per la

parte di ingresso (M) e per la parte di uscita (N). Quando tutti i valori di bi sono nulli il filtro si dice non ricorsivo altrimenti se almeno uno dei bi è diverso da zero si parla di filtro ricorsivo. Se si rappresenta il filtro con la somma (integrale) di convoluzione i filtri possono essere classificati in base alla risposta impulsiva. Un filtro FIR (Finite Impulse Response) è rappresentato da una somma di convoluzione su un numero finito di termini; un filtro IIR (Infinite Impulse Response) da una somma di convoluzione su un numero infinito di termini.

Pag. 81


FIR abitualmente realizzati in modo non ricorsivo. progetto realizzato iterativamente. risposta in fase lineare (se la risposta impulsiva è simmetrica o antisimmetrica. meno selettivi dei filtri IIR, a parità di coefficienti. maggiore flessibilità all’adeguarsi alle specifiche. IIR realizzati in modo ricorsivo. progetto realizzato con metodi chiusi. risposta in fase non lineare con quasi tutti i metodi. più selettivi dei corrispondenti FIR. più rigidi nel soddisfare le specifiche.

In genere il progetto di un filtro procede secondo lo schema seguente: • approssimazione: Determinazione della funzione di trasferimento del filtro a

partire da assegnate specifiche sull’ampiezza, fase ed eventualmente sulla risposta nel tempo • realizzazione: Strutturazione della funzione di trasferimento in elementi

circuitali. • valutazione degli errori aritmetici: Analisi delle sorgenti di errore legati alla

precisione finita nella rappresentazione dei dati e dei coefficienti del filtro nonché nel calcolo della risposta. • costruzione: Simulazione del filtro su calcolatore o sua realizzazione circuitale.

Per ogni filtro è possibile indicare il ritardo di fase e quello di gruppo così definiti:

ritardo di fase ( ) ( )τ ω

ϑ ωωf = −

ritardo di gruppo ( ) ( )τ ω

ϑ ωωg

dd

= −

Ad un ritardo di fase non dipendente da ω, ritardo di fase costante, corrisponde una risposta infrequenza con fase lineare con la pulsazione (frequenza), in pratica θ(ω)=τω.

Per un valore di N finito nella risposta impulsiva (FIR) si ha che:

( )H z h znn

n

N

= −

=

−

∑0

1

da cui

( )H e h ejn

j n

n

Nω ω= −

=

−

∑0

1

Pag. 82


Si può dimostrare (Rabiner) che per un filtro FIR con risposta impulsiva simmetrica

o antisimmetrica. ( )

τ =−N 12

T

Inoltre per una risposta impulsiva simmetrica o antisimmetrica si può scrivere la risposta in frequenza come il prodotto di una funzione reale per un esponenziale. Facendo l’ipotesi di una funzione simmetrica con N dipari si può scrivere:

( )( )

( )∑ ∑∑−

=

−

+=

−−

−−−

−

=

− ++==2

3

0

1

21

21

21

1

0

N

n

N

Nn

Nj

Nnj

nnj

n

N

n

njn

j eheheheheHωωωωω

poiché per ipotesi hn=hN-1-n si può scrivere:

( )( ) ( )

( )∑∑−

=

−−

−

=−

−−

=⎪⎭

⎪⎬

⎫

⎪⎩

⎪⎨

⎧

⎥⎦

⎤⎢⎣

⎡⎟⎠⎞

⎜⎝⎛ −

−+=

21

0

212

3

021

21

cos2

1cos2

N

kn

nj

N

nnN

Njj kaenNhheeH ωω

ωωω

dove k=(n-1)/2 ed an è definito nella tabella seguente.

hn N ( )H e jω Simmetrica

dispari ( )( )∑

−

=

−− 2

1

0

21

cos

N

kn

njkTae ω

ω

Simmetrica pari ( )

∑=

−−

⎟⎠⎞

⎜⎝⎛ −

2

1

21

)21(cos

N

kk

njTkbe ω

ω

antisimmetrica dispari ( )( )∑

−

=

−− 2

1

1

21

N

kk

njkTsinae ω

ω

antisimmetrica pari ( )

∑=

−−

⎟⎟⎠

⎞⎜⎜⎝

⎛⎟⎠⎞

⎜⎝⎛ −

2

1

21

21

N

knk

njTksinbe ω

ω

a hN0 1

2

= − a hk N

k= −

−2 1

2

b hk N

k=

−2

2

Pag. 83


5.2 Moving Average Operator (Fir Averaging Filter) Il Moving Average Operator è un filtro FIR passa-basso (smoothing filter) con

coefficienti hn=1/N n=0,1,...,N ( ) ( ) ( ) ( ) ( )( )1...211

−−++−+−+= NnxnxnxnxN

ny

La sua funzione di trasferimento nel dominio della z-trasformata è data da: ( )( ) 1

121

111...11)( −

−−−−−

−−

=++++=zz

Nzzz

NzH

NN

Posto , si ottiene la risposta in frequenza: z e j= ω

( ) ( )( )

( ) 2/1

2/sin2/sin1

111 −−

−

−

=−−

= Njj

jN

eNNe

eN

H ωω

ω

ωωω

che ha una risposta di fase lineare e zeri nelle radici nme dell’ unità 1-N1,2,...,=k ,2 ,

Nkez k

kjk

πωω ==

La frequenza di taglio del filtro può essere considerata approssimativamente il centro della base del primo lobo cioè

Ncπω = .

( ) ( )( )

( )( )

2222 2

2/2/sin1

2/sin2/sin1

πππ

ππω =≈=

NNNNN

NH

in decibel dB9.32log102

10 =⎟⎟⎠

⎞⎜⎜⎝

⎛⎟⎠⎞

⎜⎝⎛−π

0 2π/N π

1

ωc

N = 10

Figura 5.1: Risposta in frequenza del “Moving Average Operator”

Posto fmax la massima frequenza contenuta nel segnale si avrà

maxmaxmax 2/ ,/ , ffsNNc ≤≤≥ ωπωω Realizzazione ricorsiva del filtro

Pag. 84


( ) ( ) ( ) ( ) ( )( )1...211+−++−+−+= Nnxnxnxnx

Nny

( ) ( ) ( ) ( ) (( )NnxNnxnxnx )N

ny −++−++−+−=− 1...2111

( ) ( ) ( ) ( )( )NnxnxN

nyny −−+−=11

Si può anche ottenerne una versione non causale a ritardo nullo utilizzando la forma:

( ) ( ) ( ) ( ) ( ) (( )( )knxknxnxknxknx )k

ny ++−++++++−+−+

= 1......112

1

5.3 Filtro di Hanning Il filtro di Hanning è un filtro FIR passa-basso (smoothing filter) con h1= h3=1, h2=2

e d=1/4 (fattore di normalizzazione). ( ) ( ) ( ) ( )( )2*1** 321 −+−+= nxhnxhnxhdny

( ) ( ) ( ) ( )( )21*241

−+−+= nxnxnxny

La sua funzione di trasferimento nel dominio della z-trasformata è data da: ( )21*21

41)( −− ++= zzzH

Posto , si ottiene la risposta in frequenza: ωjez =( ) [ ] ( )[ ]

( ) ( ) ( ) ( )( )[ ]

( )( )[ ]

( ) ( )( )[ ]ωω

ω

ωωωω

ω

ω

ω

ωωωωω

cos121

cos2241

sin*cos2sin*cos41

24121

41 2

+=

+

=−+++

=++=++=

−

−

−−−−

H

e

jje

eeeeeH

j

j

jjjjj

Pag. 85


0 π

1

ωc=0.36*π

Figura 5.2: Risposta in frequenza del filtro di Hanning

Pag. 86


5.4 Filtri ad Approssimazione polinomiale ai minimi quadrati. L’algoritmo di approssimazione polinomiale ai minimi quadrati approssima un

insieme di punti n, comunque dispari, della sequenza di ingresso con una parabola. Per ogni nuovo punto della sequenza di ingresso si calcola una nuova approssimazione parabolica, in modo da avere una nuova parabola di n punti per ogni nuovo punto. Se si costruisce una sequenza di uscita a partire dal punto centrale di ogni parabola si ottiene un sistema con caratteristiche di filtro passa-basso. Il polinomio rappresentante la parabola per un insieme di 5 punti è:

( ) ( ) ( ) ( )nTsknTksnTskTnTp 2

210 ++=+

dove p(nT+kT) è il valore della parabola calcolato per ognuno dei 5 possibili valori

di k(-2,1,0,1,2). Le variabili s0(nT), s1(nT), e s2(nT) sono i coefficienti della parabola da calcolare. L’errore quadratico medio è dato da :

( ) ( ) ( ) ( ) ( )[ ]{ }22

22

210210 ,, ∑

−=

++−−=k

nTsknTksnTskTnTxsssε

Per minimizzare l’errore quadratico si eguaglia a zero le sue derivate rispetto ai

coefficienti della parabola:

00

=sδδε

δεδs1

0= δεδs2

0=

Si ottengono un insieme di tre equazioni nei coefficienti della parabola:

( ) ( ) (∑−=

−=++2

220 1005

kkTnTxnTsnTs )

)

)

( ) (∑−=

−=++2

21 0100

k

kTnTkxnTs

( ) ( ) (∑−=

−=++2

2

220 34010

k

kTnTxknTsnTs

risolvendo queste equazioni si ottiene:

( ) ( ) ( ) ( ) ( ) ([ ]TnTxTnTxnTxTnTxTnTxnTs 2312171223351

0 +−+++−+−−= )

( ) ( ) ( ) ( ) ([ ]TnTxTnTxTnTxTnTxnTs 2222101

1 ++++−−−−= )


2 +++−−−−−= )

Se la sequenza di uscita è data dai punti centrali(k=0) di ogni parabola calcolata si

ottiene: ( ) ( ) ( ) ( ) ( )nTsnTsknTksnTskTnTp k 002

210 =++=+ =

Pag. 87


La sequenza di uscita così calcolata è una versione filtrata della sequenza di

ingresso poiché l’approssimazione parabolica fornisce un’approssimazione smussata della sequenza di ingresso. Dalla precedente segue che l’equazione del filtro passa-basso così ottenuto è:


0 +−+++−+−−= )

e la sua risposta in frequenza è

( ) ( )TTTS ωωω 2cos6cos2417351

0 −+=

Ovviamente è possibile per questa via calcolare anche filtri su interpolazioni di 7 e più punti.

Consideriamo ore la derivata della parabola in k=0, si ottiene: ( ) ( ) ( ) ( )nTsnTksnTs

dkkTnTdp

k 1021 2 =+=−

=

Cioè la sequenza di uscita che approssima la derivata della sequenza di ingresso è data dai coefficienti s1 delle parabole calcolate. Ovviamente la sequenza di uscita che

approssima la derivata seconda è data dai coefficienti s2 delle parabole calcolate.

5.5 FAS – Fast Integer Coefficient Fir Filters I filtri FAS si basano sull’uso ripetuto del moving average operator e di operazioni

di addizione e sottrazione. Posto H(z) la funzione di trasferimento del moving average operator (operatore di smoothing) ed E(z) il segnale di ingresso si consideri la seguente procedura:

Filtraggio ( ) ( ) ( )zHzEzE =1 Sottrazione ( ) ( ) ( )E z E z E z2 1= −Filtraggio ( ) ( ) ( )E z E z H z3 2= Addizione ( ) ( ) ( )E z E z E z4 1 3= +

dove Ei è il segnale ottenuto dopo i° passo di elaborazione. La funzione di

trasferimento risultante è: ( ) ( ) ( )[ ] ( )zHzHzHzH −+= 11

Il risultato è che le componenti ad alta frequenza vengono meno attenuate mantenendo fissi gli zero del filtro. La sigla FAS indica la procedura di “Filtratio-Addition-Subtraction”. L’ operatore di smoothing può essere considerato uno filtro FAS di ordine zero. In generale la funzione di trasferimento di un FAS di ordine n è data dalla:

( ) ( ) ( )[ ]NN

N zHzHzH ∑ −=0

1

Pag. 88


Per un operatore di smoothing a cinque punti si ottiene utilizzando la forma

ricursiva non causale a ritardo nullo: ( ) ( )4321234

1 276567204.0 zzzzzzzzzH −−+++++−−= −−−−

( ) ( )65432234562 392045331933452093008.0

22 −−−−−− ++−−+++++−−++=−

zzzzzzzzzzzzzHdisegnate nella figura seguente (H0 linea a punti, H1 tratto e punto, H2 linea continua)

L’equazione alle differenze per un filtro FAS del primo ordine basato su un operatore di smoothing a cinque punti è:

( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ⎟⎟

⎠

⎞⎜⎜⎝

⎛+−+−++++

++−+−+−−−−=

432271651627324

04.01 nxnxnxnxnxnxnxnxnx

ny

a realizzazione del filtro basato su questa equazione alle differenze richiede 9 addizioni, 6 moltiplicazioni per interi ed una divisione. Utilizzando la definizione di FAS (vedi tabella) sono necessarie solo sei addizioni e due divisioni per intero. Il vantaggio di questo secondo procedimento è più ovvio per filtri FAS di ordine superiore al primo. Lo svantaggio di questa procedura è nella necessità di disporre di memoria addizionale per conservare i risultati intermedi. Nel caso di un FAS del primo ordine sono necessari due array per memorizzare E1 ed E3. In caso di elaborazioni in tempo reale si può utilizzare un equivalente equazione recursiva derivabile dalla stessa definizione. Per un FAS del primo ordine si può scrivere una procedura recursiva in quattro passi:

( ) ( ) ( ) ( )[ ] ( )( ) ( ) ( )( ) ( ) ( ) ( )[ ] ( )( ) ( ) ( )njnfny

kkngkngnjnjnfnxng

kknxknxnfnf

+=++−−−−=

−=++−−−−=

1

12/1

12/1

dove f(n), g(n) e j(n) sono i risultati intermedi ed y1 il valore filtrato. Due stack FIFO sono necessari per salvare 2k+1 valori di f(n) e j(n).

Nel campo dell’analisi dei segnali biomedici (quali ECG EOG EEG) filtri FAS di ordine zero e del primo ordine possono essere usati per eliminare l’interferenza a 50 Hz ed ottenere un effetto di “smoothing” del segnale. Un filtro FAS di ordine superiore può essere utilizzato per eliminare la sola interferenza di rete essendo l’effetto di “smoothing” molto debole.

0 0.2 0.4 0.6 0.8 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Figura 5.3: funzione di trasferimento per filtri FAS di ordine: 0 (linea a punti), 1 (linea a tratto-punto), 2 (linea continua)

Pag. 89


5.6 Filtro FIR per la rimozione dell’interferenza di rete e delle oscillazioni

della linea di base. In genere i filtri FIR non sono molto usati per la rimozione di disturbi a banda

stretta, poichè per ottenere elevata sensibilità è necessario progettare un filtro con un numero molto elevato di coefficienti. E’ possibile, in condizioni particolari ottenere una notevole riduzione del numero dei coefficienti necessari in presenza di valori particolari del rapporto tra la frequenza di campionamento e quella del disturbo.

L’uscita di un generico filtro FIR è data dalla convuluzione tra sua risposta impulsiva ed il segnale di ingresso:

( )∑−

=−=

1

01

N

iinn hxy

che richiede N somme ed N prodotti per ogni campione del segnale di uscita yn. Si immagini di trattare con un filtro un segnale limitato in banda (filtro di

antialiasing), per esempio a 125 Hz, e campionato con una frequenza di campionamento almeno pari al doppio, per esempio 250 Hz, che sia un multiplo della frequenza centrale del disturbo, per esempio l’interferenza di rete e le sue armoniche. La risposta ideale ricercata è riportata in figura .

-fk 0 fk 50-fk 50 50+fk Figura 5.4 : Risposta ideale del filtro per la rimozione del disturbo di rete e delle oscillazioni della linea di base

Per progettare un filtro FIR a numero ridotto di coefficienti che abbia una risposta reale approssimabile a quella richiesta, si parte da un filtro numerico FIR passa alto con un elevato numero di coefficienti, per esempio 91. La risposta di un tale filtro è riportata nella figura sull’asse delle frequenze per valori positivi di frequenza superiori alla massima frequenza considerata pari a metà della frequenza di campionamento. Vista in questo modo la risposta in frequenza del filtro svela la sua natura periodica, mostrando un periodo proprio pari alla frequenza di campionamento. Le caratteristiche del filtro quali ampiezza della banda di transizione, attenuazione in banda oscura, frequenza di taglio inferiore di questo filtro dipendono dal metodo di progetto utilizzato per il filtro FIR.

Pag. 90


0 f m a x f c0 .5

0 .6

0 .7

0 .8

0 .9

1

1 .1

Figura 5.5: risposta in frequenza del filtro FIR passa-alto Si procede a questo punto alla riduzione del numero dei coefficienti mantenendo la

durata della risposta impulsiva costante. Per ottenere questo risultato si utilizzano solo M coefficienti tali che valga la:

( ) ( ) TNTkM •−=••− 11 Ovviamente la trasformata della nuova risposta impulsiva ottenuta aumentando

l’intervallo temporale tra due coefficienti sarà ancora una funzione periodica ma il cui periodo sarà ora k volte più piccolo. Per il nostro esempio volendo ottenere una periodicità di 50 Hz si ha:

5150 =→•

= kTk

La risposta calcolata per N=91 e k=5 (M=18) è riportata in figura:

0 f m a x f C0 . 9

0 . 9 2

0 . 9 4

0 . 9 6

0 . 9 8

1

1 . 0 2

f c / 5 2 f c / 5 3 f c / 5 4 f c / 5 Figura 5.6: risposta in frequenza del nuovo filtro ottenuto decimando i coefficienti

Si è così ottenuto un filtro reale con risposta infrequenza molto prossima a quella

ideale richiesta. Un ulteriore riduzione del numero dei coefficienti può essere ottenuto tenedo conto

della simmetria del filtro FIR richiesta per ottenere una fase della risposta lineare almeno nella banda passante. In tal caso si può scrivere:

Pag. 91


( )kiMik hh −−= 1

da cui si ottiene per la convoluzione la seguente formula:

( )( )

∑−

+−−−−− ++•=23

0)1(

21

21

M

ikkMniknkiMMn xxhxhy

Ci siamo così ridotti a ((M-3)/2)+2 moltiplicazioni per ogni valore di y. Il filtro FIR passa-alto può essere progettato utilizzando una qualunque delle

tecniche disponibili, è comunque possibile effettuare un calcolo diretto dei coefficienti ricordando che a causa della sua periodicità la risposta in frequenza può essere espressa in somma di seni e coseni (serie di Fourier).

( ) ( ) ( )( )∑∞

=

++=1

0 2sin2cos2 n

pnpn fnTbfnTaa

fH ππ

dove Tp è il periodo di simmetria, nel nostro caso Tp=1/50=20 ms ed fp=1/Tp.=50 Hz.

In questo caso è possibile calcolare i coefficienti a partire dalla risposta in frequenza H(ejωT). I coefficienti an e bn si calcolano utilizzando le:

( ) ( )

( ) ( )∫

∫

−

−

••=

••=

2

2

2

2

2sin2

2cos2

p

p

p

p

f

f pp

n

f

f pp

n

dfnTfHf

b

dfnTfHf

a

ωπ

ωπ

A causa della simmetria della risposta in frequenza rispetto a f = 0 tutti i coefficienti bn sono nulli. Sostituendo nelle precedenti il valore di H(f)

H(f) = 0 per |f-n50|<fk H(f) = 1 altrove

si ottengono i coeffiecienti an:

( )n

Tnfa

ff

a

pkn

p

k

ππ2sin

2

210

−=

−=

Antitrasformando si ottiene una risposta impulsiva non casuale a numero infinito di coefficienti.

( )

0=nper 21

0ncon 2

p

kn

nk

n

ff

h

hn

nTfsenh

−=

≠=−= −ππ

Si osservi che essendo H(f) una funzione reale si è ottenuta una risposta inpulsiva simmetrica. Ovviamente per ottenere un filtro a risposta finita che possa essere realizzato come filtro FIR non recursivo è necessario troncare la risposta impulsiva con una finestra di lunghezza M*Tp che equivale ad imporre la condizione:

( )nM

≤−1

2

Pag. 92


La risposta impulsiva è stata troncata simmetricamente rispetto allo zero al fine di

mantenere la simmetria dell’impulso. Per ottenere un filtro causale, basta far scorrere la risposta impulsiva di (M-1)/2 punti pari a (M-1)Tp/2. Questa operazione introduce un ritardo tra ingresso ed uscita, proprio pari a (M-1)/2 punti. Dopo questa operazione la risposta in frequenza diviene:

( ) ( ) ( )fHefH t

TMfj

tp

p

212 −−

=π

dove il pedice t indica il troncamento ed il pedice p indica l’operazione di

scorrimento. La risultante risposta impulsiva diventa:

⎟⎠⎞

⎜⎝⎛−=

⎟⎠⎞

⎜⎝⎛≠=

⎟⎟⎠

⎞⎜⎜⎝

⎛⎟⎠⎞

⎜⎝⎛ −

−−= −

21-M=nper 21

21-Mncon

212

p

kn

n

k

n

ff

h

hn

TfMnsenh

π

π

Miglioramento del comportamento nella banda oscura. Per diminuire il “ripple“ in banda passante si può moltiplicare la risposta impulsiva

per una finestra, la più indicata è la finestra del Kaiser. Si ottiene allora: ( ) ( ) ( )h n h n W nw = •

dove W(n) è la finestra del Kaiser. Usando una tale finestra con il suo parametro a=28 si ottiene la riduzione del ripple ad un valore prossimo ad 1 dB picco-picco.

Miglioramento dell’attenuazione in banda oscura Il valore della risposta in frequenza nella banda oscura, pur essendo minimo, non è

in genere uguale a zero. La risposta in frequenza può essere espressa ancora, dopo la moltiplicazione per la finestra di kaiser come:

( ) ( ) ( )2

12'

pTMfj

t efHfH−−

=π

con H’(f) reale. Per ottenere che H’(0) sia nullo si può aggiungere una quantità q

tale che H(0) annulli. Per la sua periodicità H’(f) si annullerà oltre che in 0 anche per fp e 2fp . Sarà a questo punto necessario moltiplicare per un fattore 1/(1+q) per riportare al corretto valore l’ampiezza in banda-passante. Si otterrà infine :

( ) ( )( ) ( )2

12'

11 pT

MfjeqfH

qfH

−−+

+=

π

Corrispondentemente si ottiene la nuova risposta inpulsiva:

( ) ( ) ( )

( )( ) ⎟⎠⎞

⎜⎝⎛

+=

≤≤⎟⎠⎞

⎜⎝⎛

⎟⎠⎞

⎜⎝⎛≤≤

+=

21-M=nper q+nh

11

1-Mn2

1+M e 2

3-Mn0con 1

1

qh

nhq

nh

corr

corr

Pag. 93


Il fattore q può essere calcolato facilmente a partire dai coefficienti della risposta

impulsiva. Infatti dalla serie di Fourier della risposta impulsiva si ottiene per f=0 la H(f) vale:

( )H a a h hn

nm

m

nn

m

02

0

12

12

01

12

= + = −=−

−

−

=−

−

∑ ∑

ottenuta ricordando che ( ) ( )h a an02 2

0= = e h n −

da cui si ottiene la:

q h hnn

m

= −=−

−

∑01

12

.

Limitazioni sulla frequenza di taglio inferiore Ci sono alcune limitazione al valore che la frequenza di taglio inferiore può

assumere una volta fissato il valore di M. Valore suggerito dall’autore (Alste) per M è 51 con periodicità di 50Hz. In tali condizioni valori minori di 0.7 per la frequenza di taglio inferiore non sono utili perchè la risposta in frequenza ha una banda di transizione pari all’incirca a tale valore. Per valori superiori a 1.5 il “ripple” in banda-oscura tende ad aumentare rapidamente riducendo in maniera significativa l’attenuazione in banda oscura.

Un filtro di questo tipo può essere utilizzato vantaggiosamente per l’eliminazione

delle oscillazioni della linea di base e dell’interferenza di rete da un tracciato ECG senza alterarne quelle caratteristiche in bassa frequenza quali lo slivellamento S-T (tipico dell’infarto in atto).

5.7 Filtri basati su applicazioni ripetute del Moving Average Operator. La funzione di trasferimento di Moving Average Operator può essere riscritta

utilizzando il simbolo di sommatoria :

( ) ⎥⎦

⎤⎢⎣

⎡+

= ∑−

2/

2/11 M

Mm

mzM

zH

applicando N volte l’operatore si ottiene una funzione di trasferimento data dalla:

( )( )

NM

Mm

mN z

MzH ⎥

⎦

⎤⎢⎣

⎡+

= ∑−

2/

2/11

Di conseguenza il filtro è completamente definito dai parametri N ed M, dove N è il numero di volte che l’operazione di media è ripetuta ed M+1 è il numero di punti usati in ogni operazione di di media; M è scelto pari.

Usando la sostituzione si ottiene la risposta in frequenza del filtro il cui modulo è:

z e j fT= 2π

Pag. 94


( ) ( )H f

Msin M fT

sin fTN

N

=+

+11

1ππ

( )

e la cui fase è nulla. La figura seguente illustra l’effetto di M ed N sulla risposta in frequenza (A M+1=5,

N=1; B M+1=50, N=1; C M+1=5, N=2). Sebbene questa dipendenza sia molto chiara è necessario sviluppare una tecnica per la sintesi del filtro.

A

10 -3 10 -2 10 -1 10 080

60

40

20

0

B

10 -3 10 -210 -1 10 0

80

60

40

20

0

C

10 -3 10-2

10-1

10 080

60

40

20

0

Figura 5.7: risposta in frequenza per applicazioni ripetute di un moving average A)M=5 N=1 ; B) M= 50 N= 1 ; C) M= 50 N= 2 ;

Le proprietà di un filtro sono comunemente specificate in termini di attenuazione e

localizzazione delle bande passanti ed oscura. Per un filtro passa-basso la banda passante è specificata dalla frequenza di taglio superiore e dal ripple ammissibile dp e la banda oscura dalla frequenza di taglio inferiore fs e dalla attenuazione richiesta ds. La banda passante e la banda oscura sono ovviamente separate da una banda di transizione.

Pag. 95


f tp f tp

1

1-dp

ds

|H(fT)| passband stopband

Figura 5.8: risposta in frequenza di un filtro passa basso

Banda-passante. Il valore normalizzato della banda fpT è definito come la frequenza alla quale la

risposta ⎥ H(fT)⎥ è uguale al richiesto ripple 1-dp.

( ) ( )H f T

Msin M fT

sin fTdp N

N

p=+

+= −

11

11

ππ

( )

Alla frequenza fpT si ha:

sin M fTsin fT sin fT

N

N

ππ π

( )+≤

1 1

per cui si ottiene

( ) ( )1

11

1− ≤

+d

M sin fTp N

πN

risolvendo per fpT si ottiene

( )f T arcsin

M d Mpp

N≤

+ −

⎛

⎝⎜⎜

⎞

⎠⎟⎟ ≈ +

1 11 1

1 11π π

ricordando che una buona approssimazione per l’arcoseno è il suo argomento per

piccoli valori e che la radice è vicina all’unità. Per una migliore approssimazione è necessario espandere i due seni con Taylor; da

cui si ottiene:

Pag. 96


( ) ( )

( )( )( ) ( )( )

( ) ( )H f T

M

M f TM f T M f T

f Tf T f T

p N

p

p p

p

p p

N

=+

+ −+

++

−

− + −

11

11

3

1

5

3 5

3 5

3 5

ππ π

ππ π

! !...

! !...

Se si tronca la serie del numeratore a secondo termine e quella del denominatore a

primo termine si ottiene

( ) ( ) ( )

( )( )( )

H f T dM

M f TM f T

f Tp p N

pp

p

N

= − ≈+

+ −+

11

1

11

3

3

ππ

π!

che risolvendo per fpT ci fornisce una più accurata approssimazione:

( ) ( )f TM

dp N pN=

+− −

61

1 1π

ovviamente fpT risulta dipendere molto più da M che da N. Banda-oscura. Il valore normalizzato della banda fsT è definito come la frequenza alla quale la

risposta ⎥ H(fT)⎥ è uguale a zero e l’ampiezza del primo lobo laterale è definita uguale alla richiesta attenuazione ds. Per cui si ottiene:

f TMs =

+1

1

perché il numeratore della risposta in frequenze si annulla a quella frequenza. Il valore massimo del primo lobo laterale si ottiene a:

( )f TMm =

+3

2 1

perché il numeratore della risposta in frequenze è pari ad uno a quella frequenza. Sostituendo si ottiene:

( ) ( )( )

H f TM sin

M

dm N

N

s=+

+

=1

113

2 1π

L’attenuazione dipende dunque sia da N che da M. per eliminare la dipendenza da M si può valutare l’attenuazione per M tendente all’infinito:

( )( )

( )( )( )( )

MM

MN N

N

H f TM

M M

→∞ →∞=

+

+−

++

= ⎛⎝⎜⎞⎠⎟lim lim

!..

11

1

32 1

33 2 1

233

3

π π π

Pag. 97


Per valori finiti di M l’equazione fornisce una accurata approssimazione

dell’attenuazione (errore < 5% per M>6). Formule di progetto. I parametri M ed N possono dunque essere calcolati a partire da fp,dp, fs, ds

utilizzando le seguenti formule: ( ) ( )

( )

Nd

d

Mf T

d

ss

pp

N

≥⎛⎝⎜

⎞⎠⎟≈ −

≤ − −

log

log. log2

3

15

16 1 1 1

π

π−

L’ampiezza della banda di transizione così ottenuta può essere poi verificata utilizzando la:

f TMs =

+1

1

In pratica le formule di progetto funzionano bene solo se risulta accettabile che la banda di transizione sia almeno pari a mezza decade e che fp sia circa 0.1 volte la frequenza di campionamento.

Per quanto riguarda il progetto di filtri passa alto è utile ricordare che nel dominio del discreto è possibile ottenere un filtro passa alto sottraendo dalla risposta in frequenza di un passa basso l’unità Hhigh(f)=1-Hlow(f). Per le formule di progetto si ottiene:

( )N d

Mf T

p

p

= − −

= −

15 1

11

. log

Filtri passa-basso ed elimina-banda possono essere ottenuti combinando filtri passa-

basso e passa-alto.

Pag. 98


5.8 Risuonatori parametrici Un filtro risuonatore parametrico del secondo ordine è un filtro passa-banda la cui

risposta in frequenza è dominata da un singolo picco dovuto ad un polo a frequenza ω0. Per ottenere un picco a ω=ω0 , si piazza una coppia di poli complessi coniugati sui raggi a ω0 ed a - ω0 nelle locazioni complesse p=Rejω0 ed p=Re-jω0 con R modulo del polo compreso tra 0 ed 1. La funzione di trasferimento del filtro è:

( )( ) 22

11

11 111)(

00 −−−−− ++=

−−=

zazaG

zrezreGzH jj ωω

con a1 ed a2 uguali a: 2

201 a ;cos2 rra =−= ω Il valore del guadagno G può essere fissato normalizzando la massima ampiezza ad

ω0 al valore unitario cioè 1)( =zH . La risposta in frequenza del filtro si ottiene con la sostituzione ωjez =

( )( ) ωωωωωωω jjjjjj eaeaG

ereereGH 2

21111)(

00 −−−−− ++=

−−=

La normalizzazione richiede 1)( 0 =ωH

( )( ) 111

)(0000

0 =−−

=−−− ωωωω

ωjjjj ereere

GH

da cui risolvendo si ottiene ( ) ( ) 2

02cos211 rrrG +−−= ω L’ampiezza della banda a 3 dB può essere calcolata quadrando il modulo ed è pari

a: ( )r−≅∆ 12ω

- ω0

ω0

0 ω0 π/2 π

0.5

1.0

∆ω=3-dB width

Figura 5.9A: Distribuzione della coppia di poli complessi coniugati del risuonatore

Figura 5.9B: Risposta in frequenza del risuonatore

Pag. 99


( )

Per dimostrare la precedente relazione si può ricorrere ad una interpretazione geometrica della formula. Si indichino con P la posizione del polo, Q il punto in cui il raggio su cui giace P incontra la circonferenza unitaria ed A e B due punti che giacciono sulla tangente alla circonferenza in Q, con zA e zQ i numeri complessi che rappresentano i punti A e Q si può scrivere:

( )*

QQQ*

A pzpzGZH,

pzpG

−−=

−AA z

ZH−

=

Assumendo P molto vicino al cerchio unitario tutti i quattro punti P, Q, A e B sono molto vicini tra di loro e molto lontani da polo coniugato, per cui si può considerare *

Q*

A pzpz −≈− , e si ottiene:

A

Q

∆ω

P B

O

Figura 5.9 C: Interpretazione Geometrica della banda a 3 db

( )( ) PA

PQpzpz

ZHZH

A

Q

Q

A =−

−=

Per la condizione a -3 db si ottiene che ( ) ( ) 21ZH/ZH QA = , che implica 21PA/PQ = o

PQ2PA = , per cui il triangolo rettangolo PQA deve essere anche isoscele e formare un angolo in P di 45°. Allo stesso modo, si può ottenere lo stesso risultato per il triangolo PQB. Per cui si ha che ( R12PQQA2AB −=== ) . Ricordando che AB è circa uguale all’arco sotteso dall’angolo APB e che l’arco è pari al raggio (uguale ad uno) per tale angolo, angolo che rappresenta ∆ω, si ottiene che ( )R12AB −==ω∆

Pag. 100


5.9 Filtri a due Poli e due Zeri Questo è un filtro che basandosi su un unica equazione generale in forma recursiva

può generare tutti e quattro i tipo di filtro (passa-basso, passa-alto, passa-banda ed elimina-banda). L’equazione generale è data dalla:

( ) 22

11

22

11

11

−−

−−

+−++

=zbzbzazazH

con gli zeri in 2

4 2211 aaa

z−±−

=

ed i poli in 2

4 22

11 bbbz

−±−=

dove b r1 02= cosω e 22 rb =

posto s

c

ff

πω 20 = con fs frequenza di campionamento ed fc frequenza critica

(frequenza di taglio superiore per il passa-basso, frequenza di taglio inferiore per il passa-alto, la frequenza di risonanza per il passa-banda e la frequenza centrale per l’elimina-banda). La scelta di queste due frequenze vincola la posizione angolare dei poli. La scelta di r (distanza dai poli dall’origine) legata allo smorzamento (r tendente a zero risposta in ampiezza molto smorzata, r tendente ad uno risposta in ampiezza poco smorzata) fissa poi completamente la posizione dei poli e quindi i valori dei coefficienti b.

Scegliendo gli altri due coefficienti (a1 ed a2) si determina la forma del filtro vedi tabella:

a1 a2

passa-basso 2 1 passa-banda 0 -1 passa-alto -2 1 elimina banda 2cosω0 1

L’ equazione differenziale per il filtro a due poli può essere sviluppata riscrivendo

l’equazione generale

( ) ( )( ) 2

21

1

22

11

11

−−

−−

+−++

==zbzbzaza

zXzYzH

da cui si ottiene: ( ) ( ) ( ) ( ) ( ) ( ) 2

21

12

21

1−−−− +++−= zzXazzXazXzzYbzzYbzY

che nel dominio del tempo diventa: ( ) ( ) ( ) ( ) ( ) ( TnTxaTnTxanTxTnTybTnTybnTy 22 2121 − )+−++−−−=

Pag. 101


a

-ω0

ω0

0 0.2 0.4 0.6 0.8 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

b

-ω0

ω0

0 0.2 0.4 0.6 0.8 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

c

-ω0

ω0

0 0.2 0.4 0.6 0.8 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

d

-ω0

ω0

0 0.2 0.4 0.6 0.8 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Figura 5.10A: disposizione dei poli e d li i

Figura 5.10B: Risposta in frequenza

Pag. 102


5.10 Filtri a Coefficienti Interi (Integer Filter) Molto spesso per ottenere elevate velocità di calcolo si preferisce utilizzare filtri a

coefficienti interi ed evitare l’utilizzo di coefficienti in virgola mobile. Esiste una classe di filtri numerici chiamata “Integer Filter“ che prevede solo coefficienti interi nell’equazione alle differenze. Il limite di questi filtri risiede nell’impossibilità ad ottenere alcune caratteristiche specifiche come banda di transizione molto stretta.

Lynn nel 1977 ha presentato una tecnica per il progetto di filtri a coefficienti interi che è ancora molto usata. La tecnica organizzata in più passi consiste nel porre un certo numero di zeri equispaziati sul cerchio unitari. Questi zeri attenuano completamente le frequenze corrispondenti alla loro locazione. Il passo successivo consiste nello scegliere un certo numero di poli che cadono sul cerchio unitario per cancellare in maniera esatta alcuni degli zeri. Quando un polo cancella uno zero la frequenza corrispondente non è più attenuata. La localizzazione degli zeri e dei poli determina la risposta in frequenza di questi filtri. La funzione di trasferimento di questi filtri è data da:

( ) ( )( )( )

( ) ( )( )( )t

pm

t

pm

zzzzH

zzzzH

212

211

cos211

cos211

−−

−

−−

−

+−

+=

+−

−=

θ

θ

L’esponente m indica quanti zero sono piazzati sul circolo unitario; l’angolo θ indica la posizione angolare dei poli, le potenze p e t hanno attinenza con il guadagno e l’attenuazione nei lobi, per la realizzabilità del filtro devono essere non negativi. Il denominatore è dovuto ad una coppia di poli complessi coniugati che cadono esattamente sul circolo unitario. Il denominatore è dato da:

( )( ) ( ) ( ) ( ) 212 cos21 −−−−− +−=++−=−− zzeezeezezez jjjjjj ϑϑϑϑϑϑϑ Il denominatore risulta dunque a coefficienti interi solo per θ uguale a 0°, ±60°,

±90°, ±120°, ±180°. Solo se il coefficiente è intero si è sicuri di cancellare con il polo il relativo zero. Un vantaggio di questi filtri, molto utile in campo biomedico è che possiedono un andamento di fase veramente lineare e quindi un ritardo costante; questo fatto è molto utile per l’analisi di segnali biomedici per preservare l’esatta tempificazione dei picchi e/o delle caratteristiche di una forma d’onda(per es., le onde P e T ed il coplesso QRS del segnale elettrocardiografico).

La necessità di piazzare i poli a determinati valori dell’ angolo θ pone delle limitazioni al piazzamento degli zeri e contemporaneamente limita la scelta della frequenza di campionamento quando si vuole realizzare un filtro con una specifica frequenza di taglio.

Per piazzare gli zeri si usano uno dei due fattori: ( )mz −−1 o ( )1+ −z m Per tutte e due le equazioni m, intero positivo, rappresenta il numero di zeri da

piazzare sul circolo unitario. L’equazione ( )1− −z m piazza uno zero a 0° e il resto degli

Pag. 103


zeri equispaziati ad angoli di 360/m L’equazione ( )1+ −z m piazza il primo zero a 360/m e gli altri spiazzati di 360/m (vedi figura successiva).

Per ottenere un filtro stabile è necessario che il numero dei poli sia minore del numero degli zeri. E’ possibile introdurre poli nell’origine che hanno il compito di introdurre dei ritardi nel dominio del tempo. Un filtro di questo tipo può essere anche rappresentato in forma non recursiva (come un filtro FIR) non tenendo conto dei poli e degli zeri che si cancellano. Per esempio:

( ) ( )( )

13211 ...1

11 +

−

−

+++++=−−

= mm

zzzzzzzH

La soluzione non recursiva richiede in genere un numero maggiore di operazioni che la recursiva.

Filtro Passa-basso. Usando la prima delle due funzioni di trasferimento si può progettare un filtro

passa-basso pazziando un polo in z=(1,0). In realtà il denominatore produce due poli in z=(1,0).per cos(θ)=0. Si può cancellare il secondo polo con uno zero aggiuntivo o rimuoverlo. La migliore soluzione è rimuoverlo anche perché in tal modo si ottiene un algoritmo più efficiente. Si noti inoltre come sia da utilizzare il fattore e non il fattore poiché è necessario avere uno zero posizionato esattamente a 0° sul cerchio unitario. La funzione di trasferimento risultante è allora:

( )1− −z m

(1+ −z m )

( )H zzz

m

1 1

11

=−+

−

−

La risposta in frequenza di questo filtro ha un lobo in bassa frequenza di ampiezza maggiore rispetto ai lobi a frequenza più alta. La figura mostra la risposta in frequenza per m=10. Per ottenere una frequenza di taglio più bassa è necessario o utilizzare una frequenza di campionamento più bassa od introdurre altri zeri. Introdurre altri zeri è in generale la migliore soluzione anche perché aumenta la pendenza della banda di transizione. Un numero elevato di zeri può comunque comportare la presenza di segnali di uscita molto ampi, aumentando il guadagno all’aumentare del numero totale degli zeri.

Filtro Passa-alto. E’ possibile progettare un filtro passa-alto a coefficienti unitari utilizzando tecniche

differenti. La scelta del metodo appropriato dipende dalla frequenza di taglio desiderata.

Pag. 104


Soluzione per 1-z-m = 0 Soluzione per 1+z-m = 0 1-z-1 = 0 z-1 = 1 z = 1

1+z-1 = 0 z-1 = -1 z = -1

1-z-2 = 0 z-2 = 1 z2 = 1 z = 1,-1

1+z-2 = 0 z-2 = -1 z2 = -1 z= j ,-j

1-z-3 = 0 z-3 = 1 z3 = 1 z = 1, -0.5+j

0.866, -0.5 - j 0.866

1+z-3 = 0 z-3 = -1 z3 = -1 z = -1, 0,5+j 0.866, 0,5 - j 0.866

1-z-4 = 0 z-4 = 1 z4 = 1 z = 1, -1, j, -

j

1+z-4 = 0 z-4 = -1 z4 = -1 z =0.707+j

0.707 0.707-j 0.707,

-0.707+j 0.707, -0.707-j 0.707

1-z-m = 0 z-m = 1 zm = 1 z = ej2л(m/n)

1+z-m = 0 z-m = -1 zm = -1 z = ej2л[(m+1)/n]

Figura F8: disposizione degli zeri per il fattore ( )1− −z m ed il fattore ( ) 1+ −z m

Pag. 105


Metodo di progetto standard. Usando lo stesso metodo di progetto usato per il passa-basso un passa-alto può

essere progettato piazzando un polo in z=(-1,0) corrispondente a θ=180°. Il numeratore deve ovviamente avere uno zero nello stesso punto. Per m pari si userà il fattore e per m dispari il fattore (1− −z m ) ( )1+ −z m . Poiché il denominatore della funzione di trasferimento generale fornisce due poli alla locazione z=(-1,0), uno dei due deve essere rimosso. La funzione di trasferimento assume dunque una delle due forme:

( )

( )

H zzz

H zzz

m

m

1 1

2 1

1111

=−+

=++

−

−

−

−

per m pari

per m dispari

Il limite di questa tecnica è che la frequenza di taglio deve essere superiore ad un quarto della frequenza di campionamento. Aumentare il numeri di zeri riduce la banda passante. Per ottenere frequenze di taglio più basse si deve ricorrere alla tecnica della sottrazione.

Metodo di progetto basato sulla sottrazione. Un filtro passa-alto può essere progettato a partire da un filtro passa basso

sottraendo la sua uscita a quella di un filtro passa-tutto come mostrato in figura. Il filtro passa-tutto è una rete di ritardo a guadagno costante e la sua funzione di trasferimento può essere rappresentata dalla Ha(z)=Az-m dove A rappresenta il guadagno ed m il numero di zeri. I due filtri devono avere guadagno alla dc uguale, inoltre il numero di ritardi del filtro passa-tutto devono essere uguali al numero di ritardi necessari a progettare il filtro passa basso. A partire da un filtro passa-basso con molti zeri ed una frequenza di taglio superiore molto bassa si ottiene un filtro passa-alto con frequenza di taglio inferiore molto bassa.

Σ Y(z)Filtro passa-tutto

Filtro passa-basso

X(z) +-

Figura F9:

Pag. 106


Filtri Passa-banda ed elimina-banda. Un filtro passa-banda può essere facilmente progettato se si vuole una banda-

passante la frequenza centrale corrisponde ad un angolo di 60°, 90° o 120°. Se la frequenza di campionamento è scelta in modo che la frequenza centrale della banda passante cada in una di queste locazioni è possibile realizzare ponendo una coppia di poli complessi coniugati in modo che cancelli gli zeri che cadono nella banda passante. Tra il fattore ( ed il fattore )1− −z m ( )1+ −z m si sceglie quello che con un valore ragionevole di m è capace di piazzare lo zero dove necessario. Aumentando il numero di zeri (facendo crescere il valore di m) si ottiene: 1) diminuzione della larghezza della banda passante, 2) diminuzione dell’ampiezza dei lobi laterali, 3) maggiore pendenza nelle bande di transizione, 4)maggior numero di campioni da mantenere in memoria.

Un filtro elimina-banda può essere progettato o direttamente piazzando uno zero alla frequenza da cancellare o usando il metodo della sottrazione a partire da un passa-banda ed un filtro passa-tutto.

Esempio di filtro a coefficienti interi per eliminare le fluttuazioni della linea di

base e le interferenze a 50Hz e 100Hz. Questo filtro è stato presentato da Wariar ed Eswaran nel 1991 nel campo

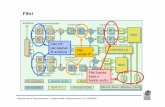
del’elettrocardiografia. Si basa sui filtri a coefficienti interi di Lynn. Un elimina 50Hz può facilmente essere ottenuto per sottrazione da un passa-banda molto stretto (Lynn). Wariar ed Eswaran hanno proposto l’utilizzo di un filtro multi-banda conosciuto come filtro estrattore capace di estrarre dal segnale la componenti a 50Hz ed a 100Hz ed inoltre le fluttazioni della linea di base. Il segnale estratto dal filtro estrattore viene poi sottratto al segnale rumoroso (ECG) come mostrato in figura.

Σ

Y(z)

Filtro passa-tuttoZ-m

Filtro estrattoreH(z)

X(z) +-

W(z)

Figura F10: modello del filtro

Pag. 107


E’ necessario che il filtro estrattore sia un filtro FIR a fase lineare che introduca un

ritardo costante per tutte le frequenze componenti. Il segnale rumoroso dovrà essere ritardato allo stesso modo prima della sottrazione. Dalla figura si ottiene:

( ) ( ) ( ) ( ) ( ) ( )zXzHzXzzYzXzzW mm −=−= −− da cui si ottiene la funzione di trasferimento risultante pari a:

( ) ( )( ) ( )zHzzXzWzP m −== −

Per meglio illustrare il comportamento del filtro si illustra la realizzazione nel caso di una frequenza di campionamento pari a 300Hz. Se si richiede che la frequenza di taglio dell’estrattore per quanto riguarda le componenti a bassa frequenza sia pari a 0.5Hz m nell’equazione precedente deve assumere il valore 300, così che 300 zeri siano piazzati sul cerchio unitario a distanza di 1Hz, e gli zeri in ωT=0, ±π/3, ±2π/3 (T=1/fs) corrispondenti alle frequenze di 0, 50, 100, 150HZ sono cancellati dai poli piazzati negli stessi punti. Si noti che il polo a 150Hz non modifica il segnale se come normalmente avviene esso è filtrato a 100Hz prima dell’acquisizione. La funzione di trasferimento è in tal caso:

( ) 1

16

300

−

−

−−

=z

zzH

che espressa in forma non-recursiva

( ) z=+z+...++149

0

6k-294288126 ∑=

−−−−+=k

zzzzH

e per la risposta in frequenza

( ) e=49

0

T6k-∑=k

TjeH ωω

Il valore di guadagno massimo raggiunto a ωT=0, ±π/3, ±2π/3 è dato da

50149

0∑=

=k

La risposta in frequenza si può scrivere: ( ) ( )

( ) ( )ωωω ωωω GTTeH Tj Tj147-Tj147- e

3sin150sine= =

0 50 100 150-50

-40

-30

-20

-10

0

10

20

30

40

50

Pag. 108


Figura F11: Parte reale della risposta in frequenza G(ω)

Il grafico della G(ω) ci mostra una rotazione non voluta di 180° a 50Hz che impedirebbe la sottrazione. Per eliminare questo problema si può o quadrare la H(z) o moltiplicarla per un fattore di correzione dato da (1+z-150). La prima soluzione porta ad un guadagno del filtro pari 50x50=2500, cosa non molto conveniente. Si preferisce dunque usare la seconda soluzione che porta ad una funzione di trasferimento pari a:

( ) ( )( ) 1

116

150300

−

−−

−+−

=z

zzzH

La cui corrispondente risposta infrequenza è data da: ( ) ( ) ( )

( )TTTeH Tj

ωωωωω

3sin75sin150sin2e= Tj222-

Il guadagno massimo nella banda passante è ora pari a 100, il livello massimo nella banda oscura è ora pari al 15.33% invece del 21.63%; il ritardo introdotto è ora pari a 222.

0 50 100 150-60

-50

-40

-30

-20

-10

0

10

Figura F12: Risposta in frequenza del filtro

Per ottenere l’equazione alle differenze che permette la realizzazione del filtro si

riscrive la funzione di trasferimento:

( ) 1

16

450300150

−

−−−

−++−

=z

zzzzH

( ) ( ) ( ) ( ) ( ) ( )6450300150 −+−−−−−+= nynxnxnxnxny

( ) ( ) ( )100

222 nynxnw −−=

Si noti come il guadagno del filtro estrattore è stato tenuto in conto dividendo y(n) per il suo guadagno (100).

Pag. 109


5.11 Derivatori Numerici Nell’elaborazione dei segnali biologici, particolarmente nel campo della

biomeccanica, è spesso necessario calcolare la derivata di una grandezza. Tipici esempi sono il calcolo di velocità ed accelerazione nello studio del cammino umano e nello studio dei movimenti oculari. Le specifiche per un derivatore per segnali biologici possono essere ricavate direttamente dalle caratteristiche stesse del segnale e del rumore ad esso sovrapposto. In generale i segnali di origine biologica hanno componenti frequenziali in bassa frequenza contaminate da rumore biologico intrinseco e da rumore esterno a banda-ampia dovuto principalmente all’uso di apparecchiature di misura. I processi di quantizzazione e di conversione introducono un rumore addizionale a larga-banda. Tale rumore è amplificato dall’operazione di differenziazione, specialmente alle frequenze più alte, ed in alcuni casi può oscurare il segnale in studio. Queste considerazioni portano all scelta di un algoritmo di differenziazione passa-basso piuttosto che ad un differenziatore a banda piena. In genere il rapporto segnale-rumore in questi casi è anche limitato, tra 60 e 80db, o equivalentemente a 10-12 bit, e il numero di campioni è relativamente piccolo, frequenza di campionamento relativamente bassa. In queste condizioni e tenendo conto che molto spesso si lavora in aritmetica a virgola fissa non ha molto senso usare algoritmo di ordine elevato. E’ preferibile in tal caso usare algoritmi di differenziazione di ordine basso.

I criteri di progetto per ottenere un filtro utile anche se di buone prestazioni possono essere così riassunte:

1) buona approssimazione della risposta in frequenza ideale alle frequenze più basse 2) un semplice filtro per le alte frequenze con un numero limitato di coefficienti. Ovviamente, la differenziazione passa-basso può essere ottenuta anche utilizzando

un filtro passa-basso e un derivatore posti in cascata. Combinare questi due stadi in un unico algoritmo di differenziazione passa basso offre migliori caratteristiche e minor tempo di calcolo. Un’altra importante specifica per un derivatore per segnali biomedici e che esso non introduca una distorsione di fase. Per questo motivo i differenziatori utilizzati in questo campo sono sistemi FIR simmetrici.

La risposta in frequenza di un filtro derivatore passa-basso ideale del primo ordine è data da:

{ απωω

πωαπα ω ≤≤=

< 0)1( )( jH (5.1)

e quella della derivata seconda è data da { απωω

πωαπα ω ≤−≤<=

0)2( 2

)(H (5.2)

dove απ (0<α≤1) indica il limite superiore della banda di differenziazione e j l’unità immaginaria.

Pag. 110


Vogliamo calcolare un filtro la cui risposta approssimi risposta ideale, restringendo

la ricerca al solo caso dei filtri numerici FIR (non ricorsivi). La risposta in frequenza per un filtro FIR approssimante il nostro filtro ideale è un polinomio in e j− ω

F H z H ez ej

j( ) ( ) ( )ω ωω= ==

−

[H(z) è la z-trasformata di {hi}, la risposta impulsiva del filtro]. Poiché la risposta in frequenza del differenziatore del primo ordine è una funzione antisimmetrica, la forma generale della risposta in frequenza del filtro approssimante si riduce a:

∑=

=N

nn nCjF

1

1 )sin()( ωω (5.3)

-π -απ-π -απ-π -απ

+π+απ

jπ

-jπ

-π -απ +π+απ

-π2

0

Figura 5.13. Andamenti della H1(ω) e della H2(ω) per un arbitrario valore di α (0<α≤1).

Poiché la risposta in frequenza per una differenziazione del secondo ordine è

simmetrica, la forma generale in questo caso è la:

∑∑==

+==N

nn

N

nn nCCnCF

1

''0

0

'2 cos cos)( ωωω (5.4)

Le corrispondenti equazioni nel dominio del tempo (ottenuta utilizzando la z-trasformata) sono:

nn

N

nnknknk CdCXXCdY •=−= ∑

=−+ dove )(

2 1

)1( (5.3’)

Yd

C X X C d Ck n k n k nn

N

n( ) ' ' '( )2

02= + =+ −

=∑ d o v e n• (5.4’)

(d è un fattore di scala scelto in modo da ottenere come coefficienti numeri interi). Poiché la risposta in frequenza del differenziatore ideale del primo ordine è una

funzione immaginaria la sua fase è π/2 per ω compreso tra zero e απ ed è -π/2 per ω

Pag. 111


compresa tra -απ e 0. Per il differenziatore del secondo ordine poiché la sua risposta in frequenza è una funzione reale negativa la fase è π su tutto l’intervallo, ωcompreso tra -απ ed απ. Per il filtro approssimante del primo ordine la fase è pari a π/2 dove la sommatoria risulta essere positiva e pari a -π/2 dove la sommatoria risulta negativa, ciò assicura che la fase del filtro approssimate è la stessa del filtro ideale almeno nella banda di differenziazione. Lo stesso risultato si ottiene per il filtro approssimate del secondo ordine ( in questo caso la fase è π).

In generale l’espressione generale di un filtro differenziatore (equazione 5.3) può

essere riscritta:

( )∑=

•==N

nn HjnCjF

1

1 )sin()( ωωω

ωωω

che indica come il nostro derivatore reale possa sempre essere visto come la cascata di un derivatore ideale, con funzione di trasferimento jω, e di un filtro passa-basso, con funzione di trasferimento H(ω). In tal caso le caratteristiche di filtro passo-basso del derivatore reale saranno quelle del passa-basso equivalente di funzione di trasferimento H(ω).

Filtro differenziatore passa-basso ottimo. Un metodo per confrontare quanto il comportamento nel dominio della frequenza di

un filtro reale si avvicini a quello ideale è usare la misura dell’errore quadratico medio così definita:

∫+

−

−=π

πα ωωωα dFHE 2)()()(

Chiaramente, per ogni α, più piccolo è E(α), meglio F(ω) approssima la risposta in frequenza ideale Hα(ω).

A questo punto, calcolando per ogni α i coefficienti {Cn} che minimizzano questa funzione di errore, possiamo costruire il miglior filtro approssimante per ogni frequenza di taglio απ. Ciò può essere fatto semplicemente differenziando E(α) rispetto ai coefficienti Cn ed eguagliando a zero.

E’ importante ricordare che l’errore minimo su tutto l’intervallo di frequenza non implica che l’errore alle basse frequenze sia minimo. In realtà questo metodo, specialmente per bassi valori di N, fornisce filtri la cui risposta in frequenza è molto lontana da quella ideale per bassi valori di ω. Nell’analisi dei segnali biologici si spesso interessati ad ottenere un differenziatore che operi in modo corretto su segnali sovracampionati (ad esempio segnale di posizione, banda di qualche decina di Hz, frequenza di campionamento maggiore di 500 Hz, tasso di sovracampionamento maggiore di 10). In tal caso è necessario che la risposta in frequenza del nostro filtro derivatore sia a minimo errore proprio nell’intervallo di frequenze centrato intorno allo zero dove è massimo il contenuto informativo del segnale. E’ dunque necessario

Pag. 112


trovare una via per ottenere una migliore approssimazione della risposta ideale Hα(ω) in quella banda anche se al prezzo di peggiorare l’errore sul resto della banda.

Per il differenziatore del primo ordine:

∑ ===

N

1=nn

0

)1(

1nC :(3) lacon accordoin o )( jd

dF

ωωω

per il differenziatore del secondo ordine

F C

d Fd

n C

nn

N

n

( ) '

( )'( )

2

01

2 2

20

2

0 0

2 2

ω

ω

ωω

==

=

= =

= − =

∑

∑

o in accordo con la (4):

o in accordo alla (4):

Minimizzando le funzioni di errore E(1) (α) o E(2) (α) sotto le precedenti condizioni,

si trovano i coefficienti del filtro ottimo per ogni valore di α. Sostituendo questi coefficienti nelle funzioni di errore E(1) (α) o E(2) (α), rispettivamente, si ottiene il minimo errore quadratico possibile per ogni valore di α. Ovviamente è sempre possibile buone approssimazioni della risposta in frequenza ideale aumentando l’ordine del filtro N, ma un filtro con N alto richiede più tempo di calcolo.

Confronto del filtro ottimo con alcuni filtri di uso comune. Nella pratica realizzazione dei derivatori per segnali biomedici si ritrovano in

letteratura, derivatori sub-ottimali, che presentano caratteristiche vicine a quelle del derivatore ottimo ma sono di più semplice realizzazione::

1) derivatore ottenuto con l’approssimazione di Lagrange (detto anche derivatore di

Newton-Cotes) 2) derivatore ottenuto con l’approssimazione polinomiale ai minimi quadrati (detto

anche derivatore di Lanczos) 3) derivatore alle differenze centrali. 4) derivatore a parametri unitari.

Per tutte e quattro le classi di derivatori riportati si può utilizzare l’equazione alle

differenze finite, qui di seguito riportata, sostituendo i coefficienti con quelli specifici di ogni derivatore, e che sono riportati nella tabella allegata.

Equazione alle differenze valida per i8 derivatori: ( ) ( )[ ]y i d C x i n x i nn

N

( ) = • + − −∑1

e la sua funzione di trasferimento H(z) è data dalla

[ ]H z d C z znn n

N

( ) = • − −∑1

e il modulo della risposta in frequenza dalla:

Pag. 113


H T d jC sin n Tn

N

( ) (ω ω= •∑1

)

Per le ultime due classi si riportano anche alcune espressioni alternative che sono molto utili ad una interpretazione alternativa del sistema filtrante.

1) Derivatore di Newton-Cotes sono ottenuti approssimando con il polinomio di Lagrange la derivata. 2) Derivatore di Lanczos

sono ottenuti approssimando con una tecnica di approssimazione polinomiale la derivata.

3) Derivatori alle differenze centrali. Una formula alternativa è data dalla

( ) ( )nT

nkxnkxky2

)( +−+=

la sua funzione di trasferimento dalla ( )nT

zzzHnn

2

−−=

ed il modulo della risposta in frequenza dalla ( )( )

H T jsin n T

nTω ω

ωω

=

Il derivatore alle differenze centrali presenta buone caratteristiche di filtraggio

per n elevato e tempi calcolo molto bassi (risposte in tempo reale anche con hardware non molto evoluto)

4) Derivatori a parametri unitari. Una formula alternativa è data dalla:

( ) ( ) ( )y nT

NT Lx x

NT Lx x

k n Nn L

L

k n Nn L

Lk n N k n N

n L

L=

+−

⎛⎝⎜

⎞⎠⎟ =

+−

+ +=−

+ −=−

+ + + −

=−∑ ∑ ∑1

2 2 11

2 1 2

la sua funzione di trasferimento dalla

( ) ( ) ( )H z

NT Lz z

NT Lz z

n N n Nn N n N

n L

L

n L

L

n L

L

=+

−⎛⎝⎜

⎞⎠⎟ =

+−

+ −+ −

=− =− =−∑ ∑ ∑1

2 2 11

2 1 2

ed il modulo della risposta in frequenza

( ) ( )

( )

H NT Lj sin N n T

NT Lj sin N n T

n L

L

n L N

Lωω

ω= +

+ <

++ ≥

⎧

⎨⎪

⎩⎪

=−

= − +

∑

∑

12 1

12 1 2 1

( )

( )

se L N

se L N

Pag. 114


Si riporta per ogni derivatore nelle tavole I e II la notazione, l’ordine, i coefficienti,

la frequenza di taglio per la quale il filtro ha il minimo errore e tale errore. In figura 14 si riporta un esempio di applicazione del filtro confrontato con un filtro di Lanczos.

TIPO notazione ordine d C1 C2 C3 C4 α0 E(α0)

1f 1 1/T 1 .603 1.472 2f 2 1/2T 0 1 .302 0.577

Differenze centrali

3f 3 1/3T 0 0 1 .201 0.287

2n 8 -1 .734 1.554 3n 45 -9 1 .789 1.472

Newton- Cotes

4n 672 -168 32 -3 .822 1.381

2l 2 1/5T 1 2 .332 0.355 3l 3 1/14T 1 2 3 .232 0.131

Lanczos

4l 4 1/30T 1 2 3 4 .179 0.062

1f3 2 1/3T 1 1 .357 0.361 2f3 3 1/6T 1 1 1 .251 0.141 2f5 4 1/10T 1 1 1 1 .197 0.069

Parametri unitari

3f3 4 1/9T 0 1 1 1 .186 0.079

2m 2 1/T .2576 .3712 .34 0.343 3m 3 1/T .0971 .1662 .1853 .24 0.126

Filtro ottimo 4m 4 1/T .0477 .0863 .1091 .1131 .19 0.060

Fig. 5.14 Risultati di una operazione di derivazione con il filtro quasi-ottimo.

La prima figura in alto rappresenta il dato grezzo, la prima in basso la derivata con ottenuta con un classico derivatore.

Pag. 115


Figura 5.15: risposte in frequenza di alcuni filtri quasi-

ottimi ed altri per il differenziatore del primo ordine. (vedi tabella nel testo)

Pag. 116

Capitolo 5: Filtri di uso comune nell’elaborazione dei ... 5.pdf · di filtro ricorsivo. Se si...

Documents

Transcript of Capitolo 5: Filtri di uso comune nell’elaborazione dei ... 5.pdf · di filtro ricorsivo. Se si...