QDM 03 Tensori

1

Simulazione Numerica dei Fenomeni di Trasporto

Necessità di introduzione dei tensori

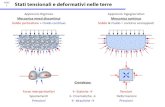
Vogliamo esprimere lo stato tensionale in un punto generico. Se consideriamo le componenti (t1, t2 e t3) del vettore sforzo t associate alle superfici normali ai versori degli assi coordinati lo sforzo complessivamente esercitato sul punto P si può esprimere mediante la terna di questi vettori.

A sua volta la generica componente (t1, t2 o t3) sarà descritta dalle tre componenti lungo gli assi del sistema di riferimento.

2



11

1213

23

21

22

Analogamente possiamo immaginare di costruire intorno al punto P un parallelepido infinitesimo e di esprimere su ogni faccia lo sforzo come somma delle tre componenti dirette secondo gli assi del sistema di riferimento

3



lo sforzo complessivo può essere dunque indicato con il seguente oggetto, chiamato tensore degli sforzi (o stress): .

333232131

323222121

313212111

3

2

1

eee

eee

eee

t

t

t

tre componenti del vettore sforzo

descritte da nove componenti del tensore degli

sforzi

≡

4


sforzo

• Il primo pedice indica la superficie attraverso la direzione normale alla stessa• Il secondo pedice la direzione lungo la quale lo sforzo è diretto

x

yz

zy

Gli sforzi in genere si indicano con oppure

solidi fluidi

5


Rappresentazione dei tensori (matrice)

333231

232221

131211

AAA

AAA

AAA

A

Una modalità di rappresentazione di un tensore si ottiene ordinando le componenti in una tabella di tre righe e tre colonne

Un tensore viene indicato in genere con una lettera maiuscola

Nello spazio a 3D un tensore può essere rappresentato da un insieme ordinato di 9 scalari

le componenti del tensore

6


Rappresentazione dei tensori (somma componenti)

Il tensore può essere rappresentato come somma di nove elementi (le componenti del tensore) ad ognuno dei quali viene associata una coppia di versori della terna di riferimento

322322221221311321121111 AAAAAA eeeeeeeeeeeeA

jiij333323321331 AAAA eeeeeeee notazione di Einstein

3

1i

3

1jjiijjiij AA eeee

7


Diade

Si definisce diade un tensore le cui componenti sono costituite da coppie ordinate delle componenti di due vettori.Ad esempio se ho due vettori v e w

La diade rappresenta quindi una sottoclasse dei tensori

3

1i

3

1jjijijiji wvwv eeeevw

Il prodotto vw è indicato come prodotto diadico

jiee vengono indicati come unità diadica

8


Calcolo tensoriale

Uno dei principali aspetti del calcolo tensoriale è lo sviluppo sistematico di notazioni formali che consentano di rendere compatta la descrizione di operazioni, trasformazioni, proprietà ... che coinvolgono i tensori

• somma di tensori• prodotto di uno scalare per un tensore• prodotto scalare di un vettore per un tensore• prodotto scalare di due tensori• doppio prodotto scalare di due tensori• prodotto vettoriale di un vettore per un tensore

Operazioni

9


Operazioni tra tensori - Somma

CBA

La somma di due tensori è un tensore che ha come componenti la somma delle componenti dei due tensori addendi

tensore del secondo ordine



Il vettore si definisce tensore del primo ordine

10


Somma tra tensori come matrici

BA

In forma di matrice si ha:

333231

232221

131211

333231

232221

131211

BBB

BBB

BBB

AAA

AAA

AAA

333332323131

232322222121

131312121111

BABABA

BABABA

BABABA

11


Somma tra tensori (somma componenti)

jiijijjiijjiij BABA eeeeeeBA

Scrivendo i tensori come somma delle componenti si ha

i j

jiijij BA ee

12


Operazioni tra tensori - Somma

Proprietà

CBACBA Associativa

ABBA Commutativa

Esiste l’elemento neutro A0A

Esiste l’elemento opposto

0A-A

13


Operazioni tra tensori – Prodotto con scalare

Il prodotto di un tensore per uno scalare

è un tensore che ha come componenti il prodotto delle componenti del tensore per lo scalare

BA

tensorescalare tensore

14


Operazioni tra tensori – Prodotto con scalare

jiijA eeA In forma di somma delle componenti

333231

232221

131211

AAA

AAA

AAA

AIn forma di matrice

15


Prodotto scalare tensore vettore

Il prodotto scalare di un tensore per un vettore da come risultato un vettore

cbA

vettoretensore vettore

Operatore lineare che trasforma un vettore in un altro vettore attraverso un prodotto scalare

definizione di tensore

16



In forma di matrice prodotto scalare righe per colonne

333232131

323222121

313212111

3

2

1

333231

232221

131211

bAbAbA

bAbAbA

bAbAbA

b

b

b

AAA

AAA

AAA

bA

3

1

3

13

2

1

3

13

3

12

3

11

i jijijijij

jj

jj

jj

jjj

jjj

jjj

bAbA

bA

bA

bA

bA

bA

bA

ee

notazione di Einstein

come matrice come somma delle componenti

17



Esprimendo il tensore come somma di 9 componenti associate alle coppie di versori il prodotto scalare risulta

i j k

kjikijk

kki j

jiij bAbA eeeeeebA

Stesso risultato di prima

ijijjkikijkkjiij bAbAbA eeeeebA

ijiji

ij

jiji j k

ijkkij bAbAbA eee

Utilizzando la notazione di Einstein si ha:

1jk se i=j 0jk se i≠j delta di kronecker

18


Prodotto scalare vettore tensore

In forma di matrice prodotto scalare righe per colonne

333232131

323222121

313212111

333231

232221

131211

321

AbAbAb

AbAbAb

AbAbAb

AAA

AAA

AAA

bbbAb

Non gode quindi della proprietà commutativa a differenza del prodotto scalare tra vettori

AbbA

333232131

323222121

313212111

bAbAbA

bAbAbA

bAbAbADiverso da quello ottenuto in

precedenza perbA

19


Prodotto scalare tra due tensori

Il prodotto scalare tra due tensori è un tensore

CBA

tensoretensore tensore

Le componenti del tensore risultante si ottengono effettuando un prodotto righe per colonne

20



333231

232221

131211

333231

232221

131211

BBB

BBB

BBB

AAA

AAA

AAA

BA

.........

.........

......BABABA 311321121111

In forma di matrici:

21



In forma di somma di componenti:

l

k lkklj

i jiij BA eeeeBA

i j

lkjiklk l

ijBA eeee

i

jkj

liklk l

ijBA ee

lijliji l

lij

jlij BABA eeee

notazione Einstein

22



liklijlkkljiij BABA eeeeeeBA

a differenza del prodotto scalare tra vettori questo non gode della proprietà commutativa. Infatti

jkklijjiijlkkl BAAB eeeeeeAB diversi!

23



Avendo trovato che

i lli

jjlijBA eeBA

Significa che la componente il del tensore risultante (C) è

j

jlijBA

Ad esempio

3

13223

jjjBAC

24


Doppio prodotto scalare

Si può definire il doppio prodotto scalare tra tensori che è uno scalare.

lkjiklijlkkljiij BABA eeeeeeeeBA ::

jiijlikjiklij BABA eeeee

BA :

tensore tensore scalare

Simbolo del doppio prodotto scalare

Si utilizza ad esempio nell’equazione di bilancio dell’energia meccanica per il calcolo del termine che esprime la conversione irreversibile dell’energia cinetica in energia interna o termica (dissipazione viscosa)

25


Prodotto vettoriale tensore vettore

Il prodotto vettoriale di un tensore per un vettore da come risultato un tensore

i l j kkijjklli vAeevA

La componente il del tensore risultante è quindi

j k

kijjklil vAB

indice di permutazione

26


Schema di sintesi delle operazioni con i tensori

Si può formulare una semplice regola per memorizzare le operazioni:Si prende il prodotto scalare o vettoriale dei due versori più vicini al simbolo dell’operazione (quelli sui due lati del simbolo) e si mette tra parentesi. Gli altri versori vanno a moltiplicare

kji eee

kji eee jkie

Esempio:

Introducendo il delta di Kronecker

kkjiij bA eeebA

1jk se i=j 0jk se i≠j

kjikij eeebAbA

27



Nel caso del doppio prodotto scalare l’operazione si ripete 2 volte prima con quelli vicini poi con quelli lontani

lkji : eeee

likj eeee

iljkIntroducendo il delta di Kronecker

lkji : eeee

28



lkji eeee

lkji eeee Introducendo il delta di Kronecker

jkli ee

Prodotto scalare tra 2 tensori

29


Schema di sintesi delle operazioni con i tensoriUtilizzando le unità diadiche è possibile costruire il seguente schema utile per memorizzare le operazioni con i tensori

iljklikjlkji : eeeeeeee

jkikjikji eeeeeee

ijkkjikji eeeeeee

jklilkjilkji eeeeeeeeee

liijkkjikji eeeeeeee

Doppio prodotto scalare T T

Prodotto scalare T v

Prodotto scalare T T

Prodotto vettoriale T v

30


Tensore nullo

Esiste il tensore nullo (0) che ha le seguenti proprietà

A0A 00

000

000

000

0

Il tensore nullo ha tutte le componenti nulle

31


Tensore unità

Il tensore unità (I) restituisce inalterato il vettore o tensore su cui opera scalarmente

aaI AAI In termini di componenti il tensore unità è esprimibile come

332211ii eeeeI

Come matrice

100

010

001

I

32


Tensore unità

Infatti se facciamo il prodotto scalare

aI

3

2

1

3

2

1

3

2

1

a

a

a

a00

0a0

00a

a

a

a

100

010

001

aI

quindi

aaI

33


Tensore isotropo

Si definisce tensore isotropo I

un tensore ottenuto dal prodotto del tensore unità per uno scalare ()

00

00

00

I

34


Tensore isotropo

Il prodotto scalare di un tensore isotropo per un vettore (b) trasforma il vettore (b) in un altro vettore (c) avente:

• stessa direzione di b• verso uguale (>0) opposto (<0) a b• modulo pari al prodotto del modulo del vettore b per lo scalare

cbI

3

2

1

3

2

1

b

b

b

b

b

b

00

00

00

35


Tensore trasposto

Dato un tensore A si definisce

tensore trasposto di ATA

tale cheTAbbA

risulta jiijA eeA jijiA eeA T

333231

232221

131211

AAA

AAA

AAA

A

332313

322212

312111

AAA

AAA

AAATA

36


Tensore trasposto

Verifichiamo cheTAbbA

333232131

323222121

313212111

3

2

1

333231

232221

131211

bAbAbA

bAbAbA

bAbAbA

b

b

b

AAA

AAA

AAA

bA

333232131

323222121

313212111

332313

322212

312111

321

bAbAbA

bAbAbA

bAbAbA

AAA

AAA

AAA

bbbTAb

Facciamo il prodotto scalare usando la notazione matriciale (il prodotto è righe per colonne)

Vettore riga si potrebbe definire come vettore trasposto del vettore colonna

37


Tensore trasposto

Si verifica che TTT ABBA

AA TT

38


Tensore simmetrico e antisimmetrico

Si definisce simmetrico un tensore uguale al suo trasporto

TAA

jiij AA Deve essere

Per un tensore simmetrico AbbA

332313

232212

131211

AAA

AAA

AAA

ATensore simmetrico

39


Tensore simmetrico e antisimmetrico

Si definisce antisimmetrico un tensore per cui

jiij AA

0Aii

0AA

A0A

AA0

2313

2312

1312

A

40


Parte simmetrica e antisimmetrica di un tensore

Ogni tensore può essere scomposto in una parte simmetrica ed una antisimmetrica

TT AAAAA 2

1

2

1

parte simmetrica parte antisimmetrica

41


Tensore inverso

Se il tensore A opera sul vettore b di modo che

bAc Si definisce tensore inverso A-1 quello che trasforma c in b

cAb -1

Si dimostra che

IAA -1 Il tensore inverso esiste solo se 0det A

QDM 03 Tensori

Documents

Transcript of QDM 03 Tensori