AlberiAlberiAlbero binarioAlbero binario

Un albero binario è un albero (ordinato) in cui ciascun nodo può avere al massimo due figli (figlio destro e figlio sinistro)

albero binario proprio: ogni nodo interno ha esattamente due figli

Strutture Dati

AlberiAlberiAlbero binario (definizione ricorsiva)Albero binario (definizione ricorsiva)

Un albero binario T o è vuoto oppure è formato da

● un nodo r detto radice;● un albero binario detto sottoalbero sinistro di T;● un albero binario detto sottoalbero destro di T.

Strutture Dati

AlberiAlberiL'ADT albero binarioL'ADT albero binario

L'ADT albero binario è un caso speciale dell'ADT albero

Metodi aggiuntivi:

left(v): restituisce il figlio sinistro di v; si verifica una condizionedi errore se v non ha il figlio sinistro

right(v): restituisce il figlio destro di v; si verifica una condizionedi errore se v non ha il figlio destro

hasLeft(v): verifica se v ha il nodo sinistro

hasRight(v): verifica se v ha il nodo destro

Strutture Dati

AlberiAlberiInterfaccia dell'ADT albero binarioInterfaccia dell'ADT albero binario

public interface BinaryTree<E> extends Tree<E>{

/** Restituisce il figlio sinistro di un nodo. */ public Position<E> left(Position<E> v) throws InvalidPositionException, BoundaryViolationException;

/** Restituisce il figlio destro di un nodo. */ public Position<E> right(Position<E> v) throws InvalidPositionException, BoundaryViolationException;

/** Ci dice se un nodo ha un figlio sinistro. */ public boolean hasLeft(Position<E> v) throws InvalidPositionException;

/** Ci dice se un nodo ha un figlio destro. */ public boolean hasRight(Position<E> v) throws InvalidPositionException;

}

Strutture Dati

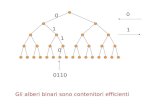
AlberiAlberiProprietà degli alberi binariProprietà degli alberi binari

Livello d: insieme dei nodi a profondità d

livello numero max di nodi

Domanda: Quanti nodi ci sono ad un dato livello i?

0 1

1

2

3

2

4

8

Risposta: ci sono al più 2 nodii

Strutture Dati

AlberiAlberiVisita inorderVisita inorder

In una visita inorder un nodo viene visitato

dopo il suo sottoalbero sinistro e

prima del suo sottoalbero destro

Algorithm inOrder(v)

if hasLeft (v)

inOrder (left (v))

visit(v)

if hasRight (v)

inOrder (right (v))

3

1

2

5

6

7 9

8

4

Strutture Dati

AlberiAlberiImplementazione mediante struttura concatenataImplementazione mediante struttura concatenata

parent

rightleft

element

riferimento alla radice

Strutture Dati

AlberiAlberiInterfaccia BTPositionInterfaccia BTPosition

public interface BTPosition<E> extends Position<E>{

public void setElement(E o);

public BTPosition<E> getLeft();

public void setLeft(BTPosition<E> v);

public BTPosition<E> getRight();

public void setRight(BTPosition<E> v);

public BTPosition<E> getParent();

public void setParent(BTPosition<E> v);

}

Strutture Dati

AlberiAlberiImplementazione di BTPositionImplementazione di BTPosition

public class BTNode<E> implements BTPosition<E>{

private E element; // l'elemento memorizzato in questo nodo private BTPosition<E> left, right, parent; // nodi adiacenti

/** Costruttore */ public BTNode(E elem, BTPosition<E> p, BTPosition<E> l, BTPosition<E> r){ element = elem; parent = p; left = l; right = r; }

...

}

Strutture Dati

AlberiAlberiImplementazione di BTPositionImplementazione di BTPosition

public class BTNode<E> implements BTPosition<E>{...

public E element() { return element; } public void setElement(E o) { element=o; } public BTPosition<E> getLeft() { return left; } public void setLeft(BTPosition<E> v) { left=v; }

public BTPosition<E> getRight() { return right; } public void setRight(BTPosition<E> v) { right=v; } public BTPosition<E> getParent() { return parent; } public void setParent(BTPosition<E> v) { parent=v; }}

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

public class LinkedBinaryTree<E> implements BinaryTree<E> { protected BTPosition<E> root; // riferimento alla radice protected int size; // numero di nodi

/** Crea un albero binario vuoto. */ public LinkedBinaryTree() { root = null; // si parte con un albero vuoto size = 0; } /** Ci dice se un nodo e` interno. */ public boolean isInternal(Position<E> v) throws InvalidPositionException { checkPosition(v); return (hasLeft(v) || hasRight(v)); }

/** Ci dice se un nodo e` una foglia. */ public boolean isExternal(Position<E> v) throws InvalidPositionException { return !isInternal(v); }

...}

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

public class LinkedBinaryTree<E> implements BinaryTree<E> {... public boolean isRoot(Position<E> v) throws InvalidPositionException { checkPosition(v); return (v == root); } /** Ci dice se un nodo ha un figlio sinistro. */ public boolean hasLeft(Position<E> v) throws InvalidPositionException { BTPosition<E> vv = checkPosition(v); return (vv.getLeft() != null); } /** Ci restituisce il figlio sinistro di un nodo. */ public Position<E> left(Position<E> v) throws InvalidPositionException, BoundaryViolationException { BTPosition<E> vv = checkPosition(v); Position<E> leftPos = vv.getLeft(); if (leftPos == null) throw new BoundaryViolationException("Non esiste un figlio sinistro"); return leftPos; }

...}

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

public class LinkedBinaryTree<E> implements BinaryTree<E> {...

...}

Strutture Dati

protected BTPosition<E> checkPosition(Position<E> v) throws InvalidPositionException { if (v == null || !(v instanceof BTPosition)) throw new InvalidPositionException("The position is invalid"); return (BTPosition<E>) v; }

protected void preorderPositions(Position<E> v, PositionList<Position<E>> pos) throws InvalidPositionException { pos.addLast(v); if (hasLeft(v)) preorderPositions(left(v), pos); // recurse on left child if (hasRight(v)) preorderPositions(right(v), pos); // recurse on right child }

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

public class LinkedBinaryTree<E> implements BinaryTree<E> {... /** Restituisce una collezione iterabile dei figli di un nodo. */ public Iterable<Position<E>> children(Position<E> v) throws InvalidPositionException { PositionList<Position<E>> children = new NodePositionList<Position<E>>(); if (hasLeft(v)) children.addLast(left(v)); if (hasRight(v)) children.addLast(right(v)); return children; } /** Restituisce una collezione iterabile dei nodi di questo albero. */ public Iterable<Position<E>> positions() { PositionList<Position<E>> positions = new NodePositionList<Position<E>>(); if(size != 0) preorderPositions(root(), positions); // assegna le posizioni secondo

// una visita preorder return positions; }

...}Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

public class LinkedBinaryTree<E> implements BinaryTree<E> {... /** Restituisce un iteratore degli elementi memorizzati nei nodi. */ public Iterator<E> iterator() { Iterable<Position<E>> positions = positions(); PositionList<E> elements = new NodePositionList<E>(); for (Position<E> pos: positions) elements.addLast(pos.element()); return elements.iterator(); // Un iteratore degli elementi }

...}

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

Abbiamo visto che la classe LinkedBinaryTree ha un costruttore che restituisce un albero binario vuoto.

A partire da questo albero binario vuoto possiamo costruire un albero binario qualsiasi

prima aggiungendo la radice e

poi via via gli altri nodi usando i seguenti metodi aggiuntivi:

● addRoot(e): crea e restituisce un nuovo nodo r contenente l'elemento e, r diventa la radice dell'albero; si ha una condizione di errore se l'albero non è vuoto

● insertLeft(v, e): crea e restituisce un nuovo nodo u contenente l'elemento e; u diventa il figlio sinistro di v; si ha una condizione di errore se v ha già il figlio sinistro

● insertRight(v, e): crea e restituisce un nuovo nodo u contenente l'elemento e; u diventa il figlio destro di v; si ha una condizione di errore se v ha già il figlio destro

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

● remove(v): rimuove il nodo v e lo sostituisce con il suo figlio (se esiste)e restituisce l'elemento memorizzato in v; si ha una condizione di errore se v ha due figli

● attach(v, T1, T2): attacca T1 e T2 rispettivamentecome sottoalbero sinistro e destro del nodo foglia v; si ha una condizione di errore se v è un nodo interno

v

w

r

a

b c

w

r

a

b c

remove(v)

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

public class LinkedBinaryTree<E> implements BinaryTree<E> {...

/** Aggiunge un nodo radice ad un albero binario vuoto. */ public Position<E> addRoot(E e) throws NonEmptyTreeException { if(!isEmpty()) throw new NonEmptyTreeException("L'albero ha già la radice."); size = 1; root = new BTNode<E>(e,null,null,null); return root; }...}

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

public class LinkedBinaryTree<E> implements BinaryTree<E> {... /** Inserisce un figlio sinistro ad un dato nodo. */ public Position<E> insertLeft(Position<E> v, E e) throws InvalidPositionException { BTPosition<E> vv = checkPosition(v); Position<E> leftPos = vv.getLeft(); if (leftPos != null) throw new InvalidPositionException("Il nodo ha gia` un figlio sinistro."); BTPosition<E> ww = new BTNode<E>(e, vv, null, null); vv.setLeft(ww); size++; return ww; }...}

vv

ww

e

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

public class LinkedBinaryTree<E> implements BinaryTree<E> {...

/** Rimuove un nodo con zero o un figlio. */ public E remove(Position<E> v) throws InvalidPositionException { BTPosition<E> vv = checkPosition(v); BTPosition<E> leftPos = vv.getLeft(); BTPosition<E> rightPos = vv.getRight(); if (leftPos != null && rightPos != null) throw new InvalidPositionException("Non posso rimuovere un nodo con due figli."); BTPosition<E> ww; if (leftPos != null) ww = leftPos; else if (rightPos != null) ww = rightPos; else // ... v è una foglia ww = null;

...}

assegna a ww il figliodi v, se esiste;se v è una foglia, ww sarà null

Strutture Dati

public class LinkedBinaryTree<E> implements BinaryTree<E> {... if (vv == root) { // se v è la radice... if (ww != null)

ww.setParent(null); root = ww; //... w diventa la nuova radice } else { // se v non è la radice... BTPosition<E> uu = vv.getParent(); if (vv == uu.getLeft())

uu.setLeft(ww); else

uu.setRight(ww); if(ww != null)

ww.setParent(uu); } size--; return v.element(); }

...}

uu

vv

uu

vv

uu

ww

uu

ww

ww ww

Strutture Dati

AlberiAlberiImplementazione di BinaryTreeImplementazione di BinaryTree

EserciziEsercizi

● Completare la classe LinkedBinaryTree che implementa l'ADT albero binario con i rimanenti metodi(insertRight, attach....)

● Si scriva un metodo BinaryTree<E> mirror (BinaryTree<E> T, Position<E> v)che, dato un albero binario T e un nodo v di T, restituisca un nuovo albero S che rappresenti la copia speculare del sottoalbero di T radicato in v.

Ad esempio, se invocato sulla radice:

a b

c

d e

r

ab

c

de

r

Strutture Dati

AlberiAlberiStampa di espressioni aritmeticheStampa di espressioni aritmetiche

Specializzazione di una visita inorder– quando visita un nodo stampa

l'operatore o l'operando corrispondente

– stampa “(“ all'inizio della visita di un sottoalbero sinistro

– stampa “)“ al termine della visita di un sottoalbero destro

Algorithm printExpression(v)

if hasLeft (v)print(“(”)

printExpression (left(v))

print(v.element ())

if hasRight (v)

printExpression (right(v))

print (“)”)

((3 (a 10)) (6 /b))

3

a 10

6 b

Strutture Dati

AlberiAlberiValutazione di espressioni aritmeticheValutazione di espressioni aritmetiche

3

a 10

6 b

Specializzazione di una visita postorder– chiamare ricorsivamente il metodo di

valutazione sui sottoalberi– quando si visita un nodo interno,

combinare i valori dei suoi sottoalberi

Algorithm evalExpr(v)

if isLeaf (v)

return v.element ()

else

x = evalExpr(leftChild (v))

y = evalExpr(rightChild (v))

<> = operatore contenuto in v

return x <> y

Strutture Dati